-
Notifications
You must be signed in to change notification settings - Fork 230
Add elliptical slice sampling algorithm #1000
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Conversation
Co-Authored-By: Cameron Pfiffer <cpfiffer@gmail.com>
|
I updated the PR and changed in particular the implementation of @model demo(x) = begin
m ~ Normal(0, 1)
x ~ MvNormal(fill(m, length(x)), sqrt(σ²))
endand @model gdemo(x, y) = begin
s ~ InverseGamma(2, 3)
m ~ Normal(0, sqrt(s))
x ~ Normal(m, sqrt(s))
y ~ Normal(m, sqrt(s))
return s, m
endsuccessfully. I created plots of the trajectories and the true (dashed blue) and approximated (orange) posterior (code): |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Thanks for the work, I left a few remarks.
|
I would suggest keeping lateral changes to another PR. Also if you are trying to compute the log likelihood, I recommend overloading |
If I understand you correctly, then you suggest using function tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, left, vi)
if left isa VarName && left in getspace(sampler)
return tilde(LikelihoodContext(), SampleFromPrior(), right, left, vi)
else
return tilde(ctx, SampleFromPrior(), right, left, vi)
end
end
function dot_tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, left, vn::VarName, vi)
if vn in getspace(sampler)
return dot_tilde(LikelihoodContext(), SampleFromPrior(), right, left, vn, vi)
else
return dot_tilde(ctx, SampleFromPrior(), right, left, vn, vi)
end
endinstead of the However, in general it seems the approach of sampling from the prior and computing the proposals in the |
|
Perhaps it would be nice if we exposed something similar to |
|
I meant something like this (only valid after #997 goes in). # assume
function tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, vn::VarName, inds, vi)
return tilde(LikelihoodContext(), SampleFromPrior(), right, vn, inds, vi)
end
# observe
function tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, left, vi)
return tilde(LikelihoodContext(), SampleFromPrior(), right, left, vi)
end
# dot_assume
function dot_tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, left, vn::VarName, inds, vi)
return dot_tilde(LikelihoodContext(), SampleFromPrior(), right, left, vn, inds, vi)
end
# dot_observe
function dot_tilde(ctx::DefaultContext, sampler::Sampler{<:ESS}, right, left, vi)
return dot_tilde(LikelihoodContext(), SampleFromPrior(), right, left, vi)
endThis takes care of the |
If it's helpful, we can have a wrapper around |
Ah OK, but then it seems it's basically what I outlined above. Your example wouldn't work, however, since the loglikelihood should be computed only based on the variable of interest. But it seems #997 would provide a simpler way to achieve what I sketched above by specifying the variables of interest |
|
@mohamed82008 This PR contains some modification to |
|
@yebai sure. |
|
@devmotion in your implementation, the log prior will be counted in for the random variables that are not under the ESS sampler. I assume this is your intention. If so, then this PR looks good to me but I can't speak on the correctness of the logic. |
Yes, that's exactly my intention. Basically, I'm interested in the log joint minus the log prior of the random variables that are sampled by the ESS sampler. A motivating example is the hierarchical model @model demo(x) = begin
m ~ Normal()
k ~ Normal(m, 0.5)
x ~ Normal(k, 0.5)
endin which we might want to sample from the posterior distribution of |
|
Great work, many thanks @devmotion! |
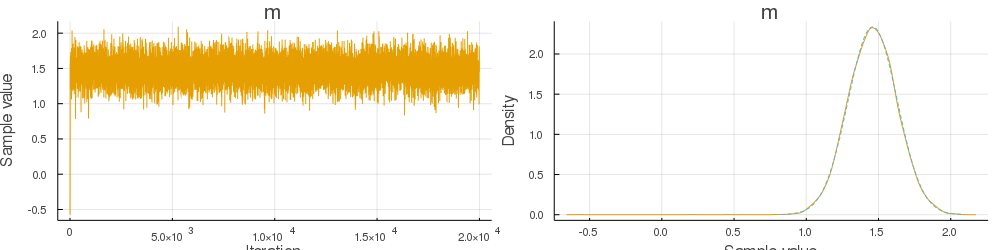
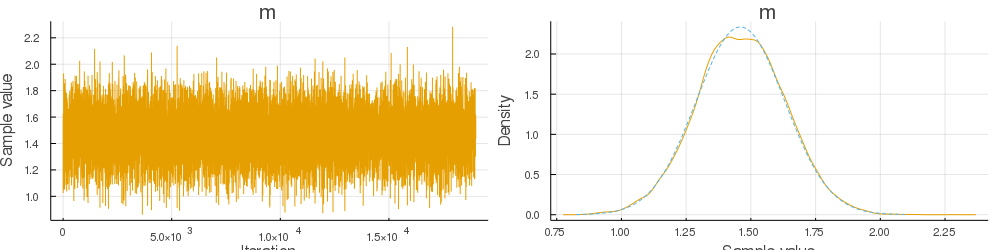
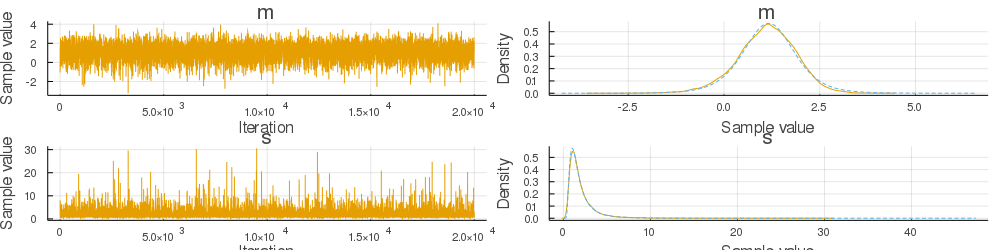
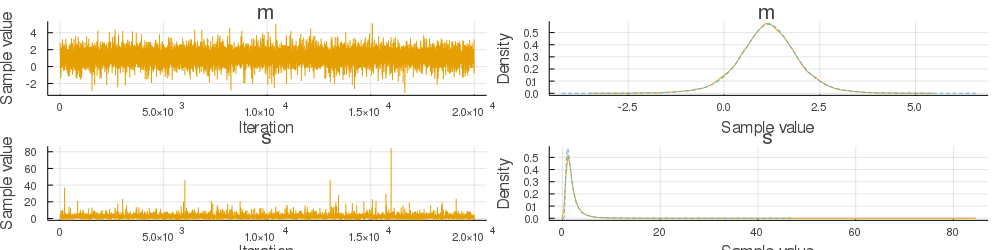
This is an updated version of the ESS in #991. I noticed that the bias visible in the plots in #991 is real and the mean of the MCMC chain does not converge to the true posterior mean. The problem was that I computed the joint probabilities although ESS requires the likelihood. I tried to fix this by changing the assume function. Moreover, I included some checks for normality and allowed only one parameter.
The example in the original issue and two other examples included in the tests seem to converge now, but the
gdemoexample still fails. I'm not sure why this is the case and assume there is some problem with how ESS is integrated in the Gibbs sampler - I guess I forgot to implement something related to Turing's internals or implemented it incorrectly.You can check the MATLAB implementation from Ian Murray, one of the original authors, for a comparison: https://homepages.inf.ed.ac.uk/imurray2/pub/10ess/elliptical_slice.m