Elliptical slice sampling

[devmotion]

Some time ago I wrote down a quick and rough implementation of the elliptical slice sampling algorithm in the Julia package EllipticalSliceSampling.jl (actually, recently I rewrote it almost completely but I haven't pushed the changes yet). Since it's a quite simple algorithm I thought it would be fun to implement an elliptical slice sampler for Turing.

I've managed to put together something that seems to work on a small and simple example. However, since I'm quite new to Turing and still don't understand all internals, I'm pretty sure my draft could be improved. Honestly, it took me quite some time to get a rough feeling for which types should be implemented and which methods should be overloaded (I think #895 (comment) was the most helpful resource I could find - thank you @cpfiffer for this write-up!). It was also surprisingly complicated to figure out how to sample from the prior and how to evaluate the log-likelihood (hopefully I actually managed to do it somewhat correctly in the end 😄 ).

I came up with the following implementation: https://gist.github.com/devmotion/6bab2561a9c340bac03c50b3fec73441#file-ess-jl Basically I tried to copy and adapt the MH implementation. However, I don't know if anything important is missing or wrong, or if some parts are not needed at all. I would be very happy if someone with a better understanding of Turing could comment on that! I'm also wondering if there is a way to avoid the repeated allocations caused by sampling from the prior? In the non-Turing implementation I used a cache to avoid these. One thing one would want to add is a check that the prior distribution is a uni- or multivariate normal distribution. Where would be the best place to do that? In the constructor of the sampler? Or in the implementation of assume?

For the simple model

@model gdemo(x) = begin
    m ~ Normal(0, 1)
    x ~ MvNormal(fill(m, length(x)), sqrt(σ²) * I)
end

and 10 random observations (you can check the code) the sampler produced the following MCMC chain of 20000 samples:

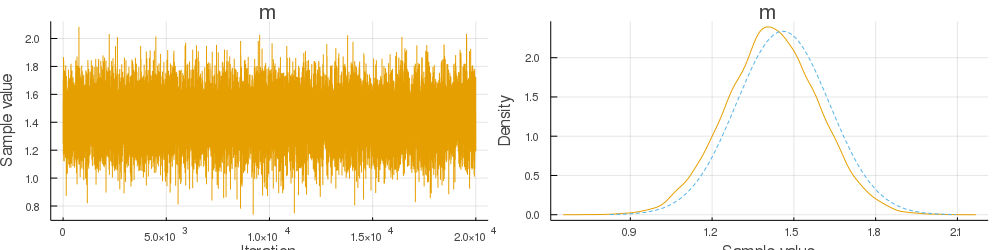
The comparison of the empirical distribution and the true posterior shows that the estimate of the mean (1.4210542073603993) is close to the true mean of the posterior (1.4597765432573337).

I'm happy to hear your comments and thoughts!

Edit: I reran the experiments since I missed that MvNormal assumes that a UniformScaling covariance is actually a matrix of standard deviations (to me that seems like a bug in Distributions).

[devmotion]

As a comparison, using NUTS() instead of ESS() gives

with an estimated mean of 1.462309997738342.

Edit: Reran this experiment as well (see above).

[mohamed82008]

I'm also wondering if there is a way to avoid the repeated allocations caused by sampling from the prior? In the non-Turing implementation I used a cache to avoid these.

In-place operations are not always good. Tracker for example doesn't support in-place mutation. That said, for non-autodiff samplers, this will be good to support. The best place to add this imo is to have a distribution type CachedDistribution that is a thin wrapper around the multivariate distribution and a cache vector, with a custom Base.rand. The user can then opt in this performance improvement by using a CachedDistribution on the rhs of ~ knowing they are opting out of Tracker-based sampling as well.

[mohamed82008]

Hmm, actually Tracker may not be an issue here. We can implement CachedDistribution anyways, and if it works fine in every case, we can consider making it the default behavior.

[devmotion]

I'm not sure if that could/should be addressed on the level of distributions. It seems that approach would be problematic if one would like to use multiple caches (e.g., if more than one sample is needed and it is not possible to override the first sample since access to both samples is required)? Maybe it would be better to solve this at the level of the algorithms/samplers and use rand! if allocations can/should be avoided? However, I'm not sure if there's a good way for constructing and saving these caches then, maybe a custom Transition would be needed? For the generation of the caches it's just a bit unfortunate that Distributions does not use the approach in stdlib and does not guarantee rand(dist) isa eltype(dist) (see also JuliaStats/Distributions.jl#882 (comment)), but one could work around that by implementing an internal rand_eltype that falls back to eltype but uses a custom implementation for the types in Distributions.

[mohamed82008]

Pre-allocation is not something we have been too concerned with in Turing so far. Most of the focus so far was on type stability, getting the interface right, supporting autodiff for various distributions, improving AdvancedHMC, and other usability issues and new features. I believe some significant gains can be made though for small models if we are more careful with allocations. However, not caching the output of the multivariate distribution is really just one drop in a sea of allocations we are doing all over the place, some of which may be avoidable, but fixing that well will require a significant effort. Currently, I don't know if such refactor is a good idea. Perhaps, after we have broken down Turing a bit more, abstracting away the internals to DynamicPPL, we can consider more aggressive pre-allocation. I will be working on DynamicPPL during the Christmas.

As for caching multiple samples, I am not sure when this can show up or how to support it. So please open another issue to think more about it with some MWE that does the problematic allocation and is not solved by CachedDistribution. But I think for most algos we have in Turing, caching just one value may be good enough. For most algos, I think we just need a temporary place to store the output of rand to compute logpdf or to write it to vi::VarInfo later. Again, I doubt this will improve things significantly given that we have many other allocations, but it may be a good start.

[devmotion]

Sure, I'll think about it but I guess it's not the most urgent problem. Coming back to my initial post, can anyone comment on any of the other questions?

Basically I tried to copy and adapt the MH implementation. However, I don't know if anything important is missing or wrong, or if some parts are not needed at all. I would be very happy if someone with a better understanding of Turing could comment on that! [...] One thing one would want to add is a check that the prior distribution is a uni- or multivariate normal distribution. Where would be the best place to do that? In the constructor of the sampler? Or in the implementation of assume?

Is there anything wrong or suboptimal with my implementation of the slice sampler? And in case you think it's fine, where should I put the code? In an external repository? In my package using Requires?

[mohamed82008]

The implementation looks alright I think. @cpfiffer might be able to comment better. If you want, make a new file in the inference folder and add it there.

[cpfiffer]

Yeah, I see nothing wrong with this implementation. It's pretty well done as far as the interface is concerned.

If you want to check whether all the distributions are normal, the easiest place would just be in the assume statement -- you could throw an error if it wasn't normal. This does have a little overhead through, since you end up checking every time you make an assume call. Adding checks to the sampler constructor seems more "right" but it would require a little more work to get the distributions ahead of time.

[mohamed82008]

Yes assume would be the right place for the check, sorry missed that question. I don't think there will be any runtime overhead to the check though because it only uses compile-time information so the compiler will elide it.

[devmotion]

I agree, these checks should compile away since they are type based.