
To search for the ground state, call randomize_spins! and minimize_energy! in sequence. For this problem, optimization converges rapidly to the expected Néel order. See this with plot_spins, where spins are colored according to their global $z$-component.
randomize_spins!(sys)
minimize_energy!(sys)
-plot_spins(sys; color=[S[3] for S in sys.dipoles])
The diamond lattice is bipartite, allowing each spin to perfectly anti-align with its 4 nearest-neighbors. Each of these 4 bonds contribute $-J s^2$ to the total energy. Two sites participate in each bond, so the energy per site is $-2 J s^2$. Check this by calling energy_per_site.
@assert energy_per_site(sys) ≈ -2J*(3/2)^2The most compact magnetic cell for this Néel order is a primitive unit cell. Reduce the magnetic cell size using reshape_supercell, where columns of the shape matrix are primitive lattice vectors as multiples of the conventional cubic lattice vectors $(𝐚_1, 𝐚_2, 𝐚_3)$. One could alternatively use shape = cryst.latvecs \ cryst.prim_latvecs. Verify that the energy per site is unchanged after the reshaping the supercell.
shape = [0 1 1;
+plot_spins(sys; color=[S[3] for S in sys.dipoles])
The diamond lattice is bipartite, allowing each spin to perfectly anti-align with its 4 nearest-neighbors. Each of these 4 bonds contribute $-J s^2$ to the total energy. Two sites participate in each bond, so the energy per site is $-2 J s^2$. Check this by calling energy_per_site.
@assert energy_per_site(sys) ≈ -2J*(3/2)^2The most compact magnetic cell for this Néel order is a primitive unit cell. Reduce the magnetic cell size using reshape_supercell, where columns of the shape matrix are primitive lattice vectors as multiples of the conventional cubic lattice vectors $(𝐚_1, 𝐚_2, 𝐚_3)$. One could alternatively use shape = cryst.latvecs \ cryst.prim_latvecs. Verify that the energy per site is unchanged after the reshaping the supercell.
shape = [0 1 1;
1 0 1;
1 1 0] / 2
sys_prim = reshape_supercell(sys, shape)
-@assert energy_per_site(sys_prim) ≈ -2J*(3/2)^2Plotting sys_prim shows the two spins within the primitive cell, as well as the larger conventional cubic cell for context.
plot_spins(sys_prim; color=[S[3] for S in sys_prim.dipoles])
With this primitive cell, we will perform a SpinWaveTheory calculation of the structure factor $\mathcal{S}(𝐪,ω)$. The measurement ssf_perp indicates projection of the spin structure factor $\mathcal{S}(𝐪,ω)$ perpendicular to the direction of momentum transfer, as appropriate for unpolarized neutron scattering. The isotropic FormFactor for Co²⁺ dampens intensities at large $𝐪$.
formfactors = [1 => FormFactor("Co2")]
+@assert energy_per_site(sys_prim) ≈ -2J*(3/2)^2Plotting sys_prim shows the two spins within the primitive cell, as well as the larger conventional cubic cell for context.
plot_spins(sys_prim; color=[S[3] for S in sys_prim.dipoles])
With this primitive cell, we will perform a SpinWaveTheory calculation of the structure factor $\mathcal{S}(𝐪,ω)$. The measurement ssf_perp indicates projection of the spin structure factor $\mathcal{S}(𝐪,ω)$ perpendicular to the direction of momentum transfer, as appropriate for unpolarized neutron scattering. The isotropic FormFactor for Co²⁺ dampens intensities at large $𝐪$.
formfactors = [1 => FormFactor("Co2")]
measure = ssf_perp(sys_prim; formfactors)
swt = SpinWaveTheory(sys_prim; measure)SpinWaveTheory [Dipole mode]
2 atoms
@@ -37,8 +37,8 @@
[0, 0, 0] → [1/2, 0, 0] → [1/2, 1/2, 0] → [0, 0, 0]
Calculate single-crystal scattering intensities along this path, for energies between 0 and 6 meV. Use plot_intensities to visualize the result.
energies = range(0, 6, 300)
res = intensities(swt, path; energies, kernel)
-plot_intensities(res; units, title="CoRh₂O₄ LSWT")
Sometimes experimental data is only available as a powder average, i.e., as an average over all possible crystal orientations. Use powder_average to simulate these intensities. Each $𝐪$-magnitude defines a spherical shell in reciprocal space. Consider 200 radii from 0 to 3 inverse angstroms, and collect 2000 random samples per spherical shell. As configured, this calculation completes in about two seconds. Had we used the conventional cubic cell, the calculation would be an order of magnitude slower.
radii = range(0, 3, 200) # (1/Å)
+plot_intensities(res; units, title="CoRh₂O₄ LSWT")
Sometimes experimental data is only available as a powder average, i.e., as an average over all possible crystal orientations. Use powder_average to simulate these intensities. Each $𝐪$-magnitude defines a spherical shell in reciprocal space. Consider 200 radii from 0 to 3 inverse angstroms, and collect 2000 random samples per spherical shell. As configured, this calculation completes in about two seconds. Had we used the conventional cubic cell, the calculation would be an order of magnitude slower.
radii = range(0, 3, 200) # (1/Å)
res = powder_average(cryst, radii, 2000) do qs
intensities(swt, qs; energies, kernel)
end
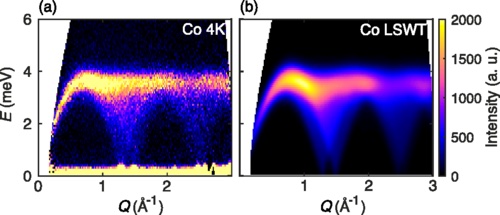
-plot_intensities(res; units, saturation=1.0, title="CoRh₂O₄ Powder Average")
This result can be compared to experimental neutron scattering data from Fig. 5 of Ge et al.
Settings
This document was generated with Documenter.jl version 1.7.0 on Thursday 10 October 2024. Using Julia version 1.10.5.