Update

README.md

@@ -147,6 +147,7 @@
     * [回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)
     * [回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
     * [回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
+    * [本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)
 
 （持续更新中....）
 

problems/0090.子集II.md

@@ -77,6 +77,39 @@ public:
 
 ```
 
+使用set去重的版本。
+```
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
+        result.push_back(path);
+        unordered_set<int> uset;
+        for (int i = startIndex; i < nums.size(); i++) {
+            if (uset.find(nums[i]) != uset.end()) {
+                continue;
+            }
+            uset.insert(nums[i]);
+            path.push_back(nums[i]);
+            backtracking(nums, i + 1, used);
+            path.pop_back();
+        }
+    }
+
+public:
+    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
+        result.clear();
+        path.clear();
+        vector<bool> used(nums.size(), false);
+        sort(nums.begin(), nums.end()); // 去重需要排序
+        backtracking(nums, 0, used);
+        return result;
+    }
+};
+
+```
+
 # 总结 
 
 其实这道题目的知识点，我们之前都讲过了，如果之前讲过的子集问题和去重问题都掌握的好，这道题目应该分分钟AC。

problems/回溯算法去重问题的另一种写法.md

@@ -0,0 +1,240 @@
+
+
+> 在 [本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA) 中一位录友对 整颗树的本层和同一节点的本层有疑问，也让我重新思考了一下，发现这里确实有问题，所以专门写一篇来纠正，感谢录友们的积极交流哈！ 
+
+接下来我再把这块再讲一下。
+
+在[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中的去重和 [回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中的去重 都是 同一父节点下本层的去重。
+
+[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)也可以使用set针对同一父节点本层去重，但子集问题一定要排序，为什么呢？ 
+
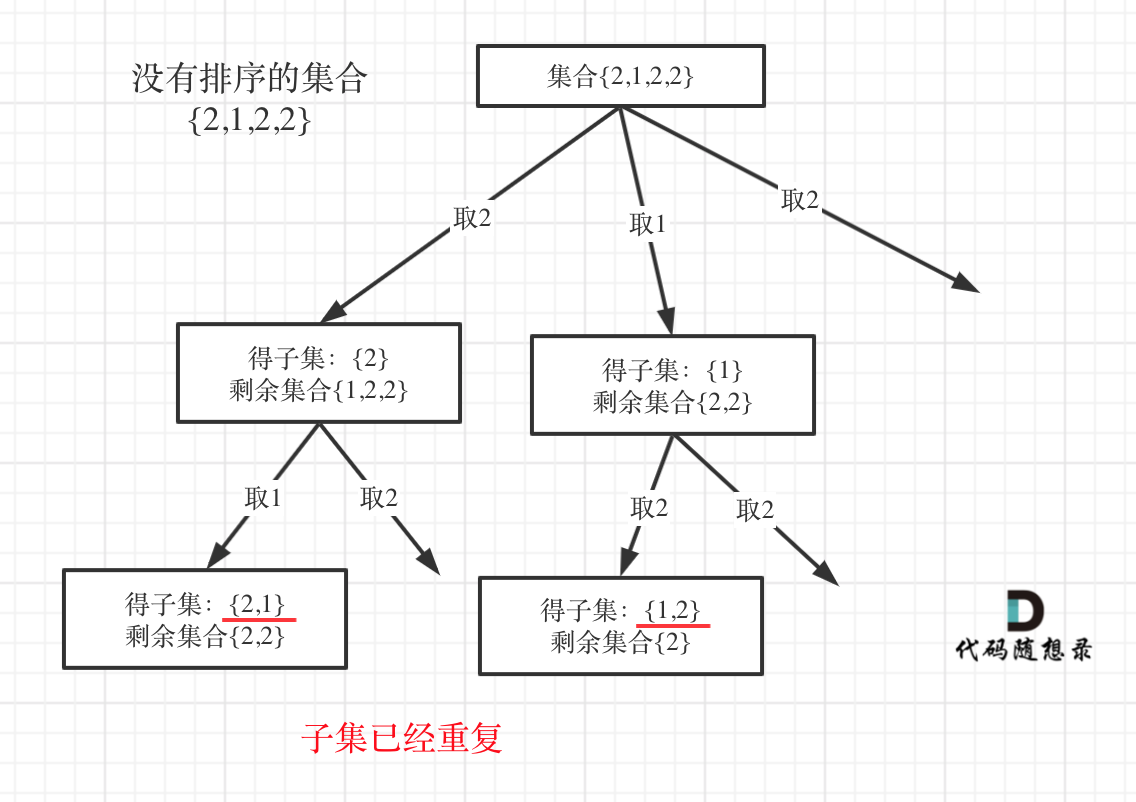
+我用没有排序的集合{2,1,2,2}来举例子画一个图，如图：
+
+![90.子集II2](https://img-blog.csdnimg.cn/2020111316440479.png)
+
+图中，大家就很明显的看到，子集重复了。
+
+那么下面我针对[回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ) 给出使用set来对本层去重的代码实现。
+
+# 90.子集II 
+
+used数组去重版本： [回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
+
+使用set去重的版本如下：
+
+```C++
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
+        result.push_back(path);
+        unordered_set<int> uset; // 定义set对同一节点下的本层去重
+        for (int i = startIndex; i < nums.size(); i++) {
+            if (uset.find(nums[i]) != uset.end()) { // 如果发现出现过就pass
+                continue;
+            }
+            uset.insert(nums[i]); // set跟新元素
+            path.push_back(nums[i]);
+            backtracking(nums, i + 1, used);
+            path.pop_back();
+        }
+    }
+
+public:
+    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
+        result.clear();
+        path.clear();
+        vector<bool> used(nums.size(), false);
+        sort(nums.begin(), nums.end()); // 去重需要排序
+        backtracking(nums, 0, used);
+        return result;
+    }
+};
+
+```
+
+针对留言区录友们的疑问，我再补充一些常见的错误写法，
+
+
+## 错误写法一 
+
+把uset定义放到类成员位置，然后模拟回溯的样子 insert一次，erase一次。 
+
+例如：
+
+```C++
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    unordered_set<int> uset; // 把uset定义放到类成员位置
+    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
+        result.push_back(path);
+
+        for (int i = startIndex; i < nums.size(); i++) {
+            if (uset.find(nums[i]) != uset.end()) {
+                continue;
+            }
+            uset.insert(nums[i]);   // 递归之前insert 
+            path.push_back(nums[i]);
+            backtracking(nums, i + 1, used);
+            path.pop_back();
+            uset.erase(nums[i]);    // 回溯再erase
+        }
+    }
+
+```
+
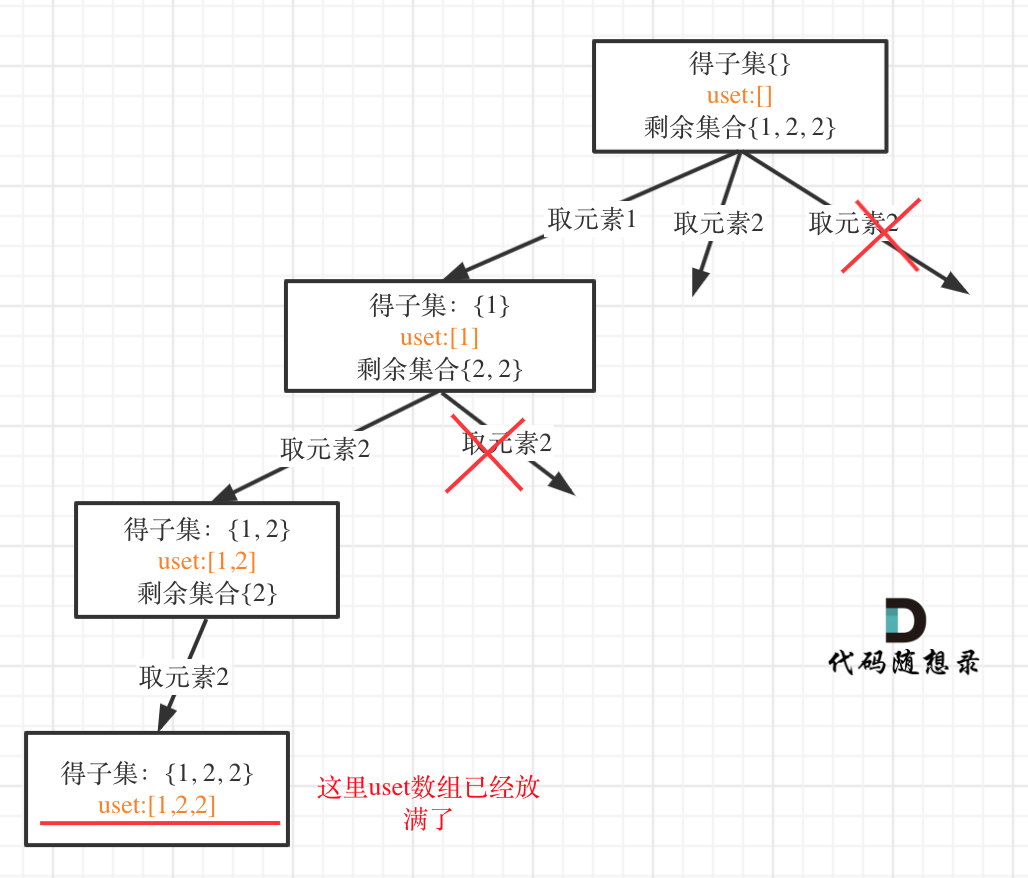
+在树形结构中，**如果把unordered_set<int> uset放在类成员的位置（相当于全局变量），就把树枝的情况都记录了，不是单纯的控制某一节点下的同一层了**。
+
+如图：
+
+![90.子集II1](https://img-blog.csdnimg.cn/202011131625054.png)
+
+可以看出一旦把unordered_set<int> uset放在类成员位置，它控制的就是整棵树，包括树枝。
+
+**所以这么写不行！** 
+
+## 错误写法二
+
+有同学把 unordered_set<int> uset; 放到类成员位置，然后每次进入单层的时候用uset.clear()。
+
+代码如下：
+
+```C++
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    unordered_set<int> uset; // 把uset定义放到类成员位置
+    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
+        result.push_back(path);
+        uset.clear(); // 到每一层的时候，清空uset
+        for (int i = startIndex; i < nums.size(); i++) {
+            if (uset.find(nums[i]) != uset.end()) {
+                continue;
+            }
+            uset.insert(nums[i]); // set记录元素
+            path.push_back(nums[i]);
+            backtracking(nums, i + 1, used);
+            path.pop_back();
+        }
+    }
+```
+uset已经是全局变量，本层的uset记录了一个元素，然后进入下一层之后这个uset（和上一层是同一个uset）就被清空了，也就是说，层与层之间的uset是同一个，那么就会相互影响。
+
+**所以这么写依然不行！**
+
+**组合问题和排列问题，其实也可以使用set来对同一节点下本层去重，下面我都分别给出实现代码**。
+
+# 40. 组合总和 II 
+
+使用used数组去重版本：[回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
+
+使用set去重的版本如下：
+
+```C++
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
+        if (sum == target) {
+            result.push_back(path);
+            return;
+        }
+        unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
+        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
+            if (uset.find(candidates[i]) != uset.end()) {
+                continue;
+            }
+            uset.insert(candidates[i]); // 记录元素
+            sum += candidates[i];
+            path.push_back(candidates[i]);
+            backtracking(candidates, target, sum, i + 1); 
+            sum -= candidates[i];
+            path.pop_back();
+        }
+    }
+
+public:
+    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
+        path.clear();
+        result.clear();
+        sort(candidates.begin(), candidates.end());
+        backtracking(candidates, target, 0, 0);
+        return result;
+    }
+};
+```
+
+# 47. 全排列 II 
+
+使用used数组去重版本：[回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
+
+使用set去重的版本如下：
+
+```C++
+class Solution {
+private:
+    vector<vector<int>> result;
+    vector<int> path;
+    void backtracking (vector<int>& nums, vector<bool>& used) {
+        if (path.size() == nums.size()) {
+            result.push_back(path);
+            return;
+        }
+        unordered_set<int> uset; // 控制某一节点下的同一层元素不能重复
+        for (int i = 0; i < nums.size(); i++) {
+            if (uset.find(nums[i]) != uset.end()) {
+                continue;
+            }
+            if (used[i] == false) {
+                uset.insert(nums[i]); // 记录元素  
+                used[i] = true;
+                path.push_back(nums[i]);
+                backtracking(nums, used);
+                path.pop_back();
+                used[i] = false;
+            }
+        }
+    }
+public:
+    vector<vector<int>> permuteUnique(vector<int>& nums) {
+        result.clear();
+        path.clear();
+        sort(nums.begin(), nums.end()); // 排序
+        vector<bool> used(nums.size(), false);
+        backtracking(nums, used);
+        return result;
+    }
+};
+```
+
+# 两种写法的性能分析 
+
+需要注意的是：**使用set去重的版本相对于used数组的版本效率都要低很多**，大家在leetcode上提交，能明显发现。
+
+原因在[回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中也分析过，主要是因为程序运行的时候对unordered_set 频繁的insert，unordered_set需要做哈希映射（也就是把key通过hash function映射为唯一的哈希值）相对费时间，而且insert的时候其底层的符号表也要做相应的扩充，也是费时的。
+
+**而使用used数组在时间复杂度上几乎没有额外负担！**
+
+**使用set去重，不仅时间复杂度高了，空间复杂度也高了**，在[本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)中分析过，组合，子集，排列问题的空间复杂度都是O(n)，但如果使用set去重，空间复杂度就变成了O(n^2)，因为每一层递归都有一个set集合，系统栈空间是n，每一个空间都有set集合。
+
+那有同学可能疑惑 用used数组也是占用O(n)的空间啊？ 
+
+used数组可是全局变量，每层与每层之间公用一个used数组，所以空间复杂度是O(n + n)，最终空间复杂度还是O(n)。
+
+# 总结 
+
+本篇本打算是对[本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)的一个点做一下纠正，没想到又写出来这么多！
+
+**这个点都源于一位录友的疑问，然后我思考总结了一下，就写着这一篇，所以还是得多交流啊！**
+
+如果大家对「代码随想录」文章有什么疑问，尽管打卡留言的时候提出来哈，或者在交流群里提问。
+
+**其实这就是相互学习的过程，交流一波之后都对题目理解的更深刻了，我如果发现文中有问题，都会在评论区或者下一篇文章中即时修正，保证不会给大家带跑偏！**
+
+就酱，「代码随想录」一直都是干货满满，公众号里的一抹清流，值得推荐给身边的每一位同学朋友！
+

problems/贪心算法理论基础.md

@@ -12,20 +12,19 @@
 在举一个例子如果是 有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，一定不行。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
 
 
-
 很多同学做贪心的题目的时候，想不出来是贪心，想知道有没有什么套路可以一看看出来是贪心，说实话贪心算法并没有固定的套路。
 
 所以唯一的难点就是如何通过局部最优，推出整体最优。 
 
-那么如何能看出局部最优是否能退出整体最优呢？有没有什么固定策略呢？
+那么如何能看出局部最优是否能退出整体最优呢？有没有什么固定策略或者套路呢？
 
-不好意思，也没有，靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能需要动态规划。
+**不好意思，没有！** 靠自己手动模拟，如果模拟可行，就可以试一试贪心策略，如果不可行，可能需要动态规划。
 
 验证可不可以用贪心最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。
 
 那又有同学认为手动模拟，举例子得出的结论不靠谱，想要严格的数学证明。 
 
-数学证明一般可以是
+数学证明一般可以是：
 
 * 数学归纳法
 * 反证法
@@ -34,13 +33,13 @@
 
 所以做了贪心题目的时候大家就会发现，如果啥都要数学证明一下，就是把简单问题搞复杂了。
 
-面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说就行。
+**面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说就行**。
 
 举一个不太恰当的例子：我要用一下1+1 = 2，但我要先证明1+1 为什么等于2。严谨是严谨了，但没必要。
 
-虽然这个例子有点极端，但可以表达这么个意思，就是手动模拟一下感觉可以局部最优推出整体最优，那么就试一试贪心。
+虽然这个例子有点极端，但可以表达这么个意思：就是手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。
 
-例如刚刚举的拿钞票的例子，就是模拟一下每次那做大的，最后就能拿到最多的钱，这还要数学证明的话，是不是感觉有点怪怪的。
+**例如刚刚举的拿钞票的例子，就是模拟一下每次那做大的，最后就能拿到最多的钱，这还要数学证明的话，其实就不在算法面试的范围内了，可以看看专业的数学书籍！**
 
 所以这也是为什么有的通过AC（accept）了一些贪心的题目，但都不知道自己用了贪心算法，因为贪心有时候就是常识性的推导，所以会认为本就应该这么做！