PyAFV

Python code that implements the active-finite-Voronoi (AFV) model in 2D. The AFV framework was introduced and developed in, for example, Refs. [1–3].

Installation

PyAFV is available on PyPI and can be installed using pip directly:

pip install pyafv

The package supports Python ≥ 3.10 and < 3.15, including Python 3.14t (the free-threaded, no-GIL build). To verify that the installation was successful and that the correct version is installed, run the following in Python:

import pyafv
print(pyafv.__version__)

On HPC clusters, global Python path can contaminate the runtime environment. You may need to clear it explicitly using unset PYTHONPATH or prefixing the pip command with PYTHONPATH="".

Install from source

Installing from source can be necessary if pip installation does not work. First, download and unzip the source code, then navigate to the root directory of the package and run:

pip install .

Note: A C/C++ compiler is required if you are building from source, since some components of PyAFV are implemented in Cython for performance optimization.

Windows MinGW GCC

If you are using MinGW GCC (rather than MSVC) on Windows, to build from the source code, add a setup.cfg at the repository root before running pip install . with the following content:

# setup.cfg
[build_ext]
compiler=mingw32

Install offline

If you need to install PyAFV on a machine without internet access, you can download the corresponding wheel file from PyPI and transfer it to the target machine, and then run the following command to install using pip:

pip install pyafv-<version>-<platform>.whl

Alternatively, you can build PyAFV from source as described in the previous section. In this case, in addition to the required prerequisites of the package, the build-time dependencies hatchling and hatch-cython must also be available.

Usage

Here is a simple example to get you started, demonstrating how to construct a finite-Voronoi diagram (click the Google Colab badge above to run the notebook directly):

import numpy as np
import pyafv as afv

N = 100                                          # number of cells
pts = np.random.rand(N, 2) * 10                  # initial positions
params = afv.PhysicalParams()                    # use default parameter values
sim = afv.FiniteVoronoiSimulator(pts, params)    # initialize the simulator
sim.plot_2d(show=True)                           # visualize the Voronoi diagram

To compute the conservative forces and extract detailed geometric information (e.g., cell areas, vertices, and edges), call:

diag = sim.build()

The returned object diag is a Python dict containing these quantities.

Simulation previews

Below are representative simulation snapshots generated using the code:

Model illustration	Periodic boundary conditions

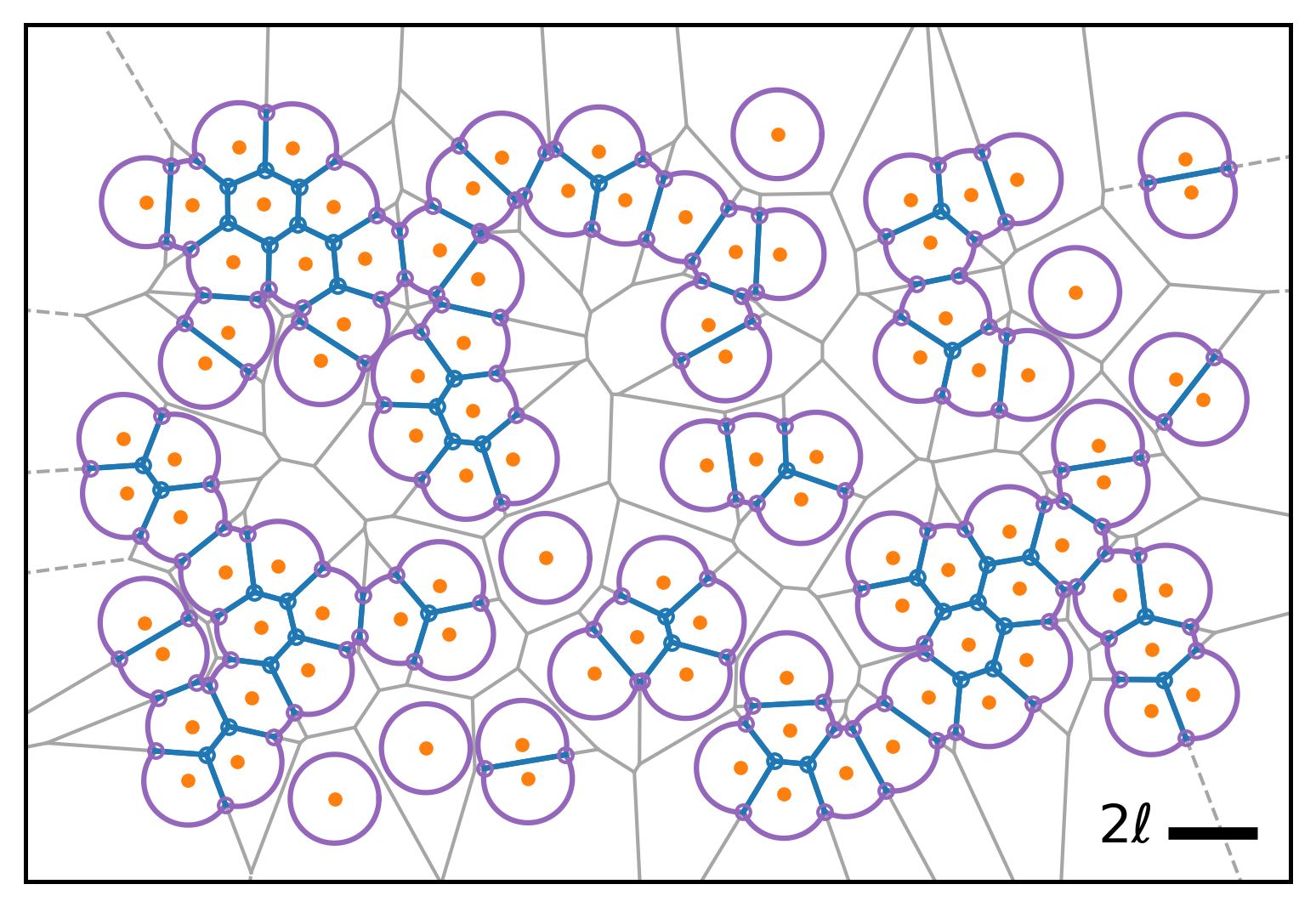Initial configuration	After relaxation	Active dynamics enabled

More information

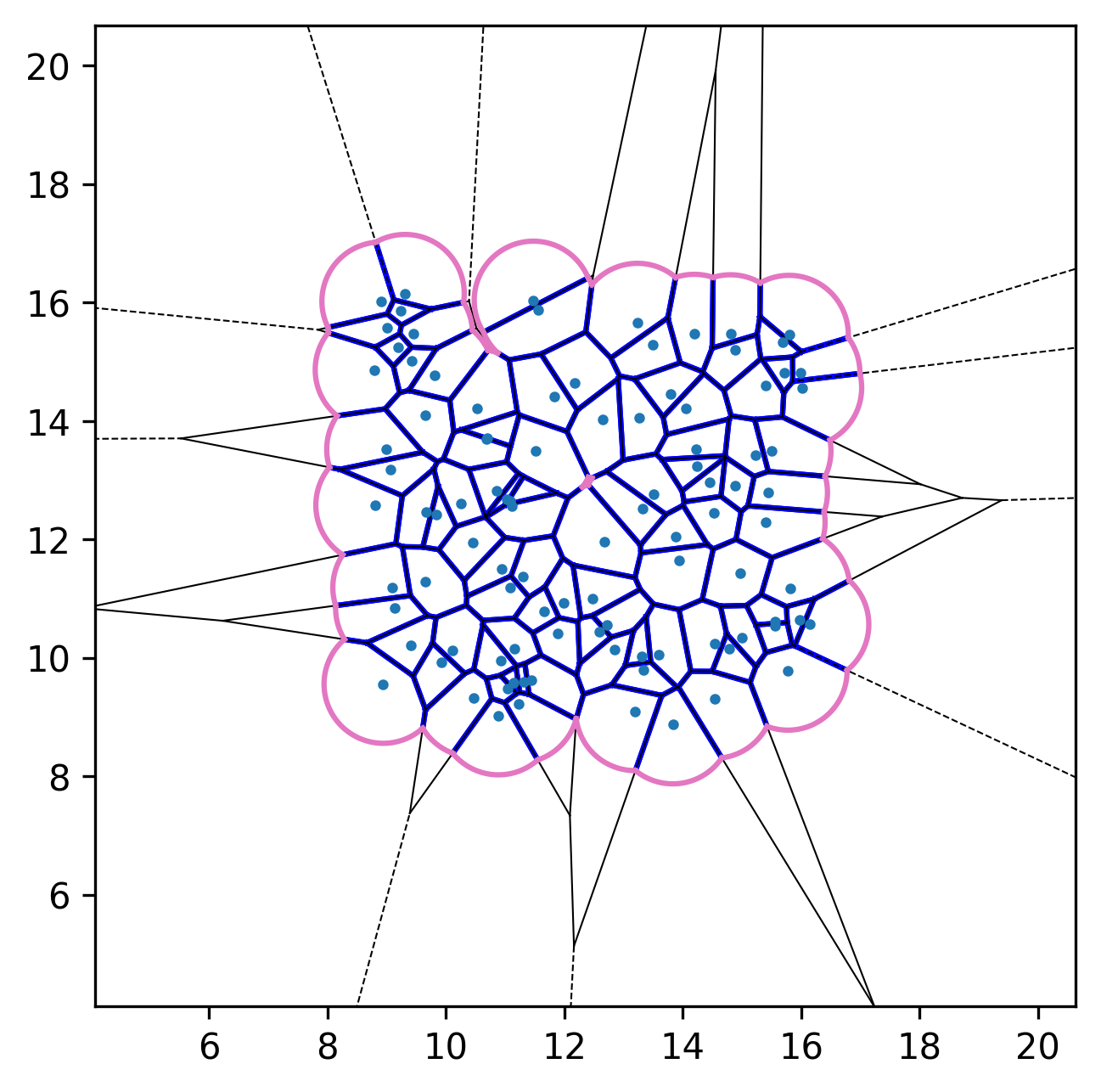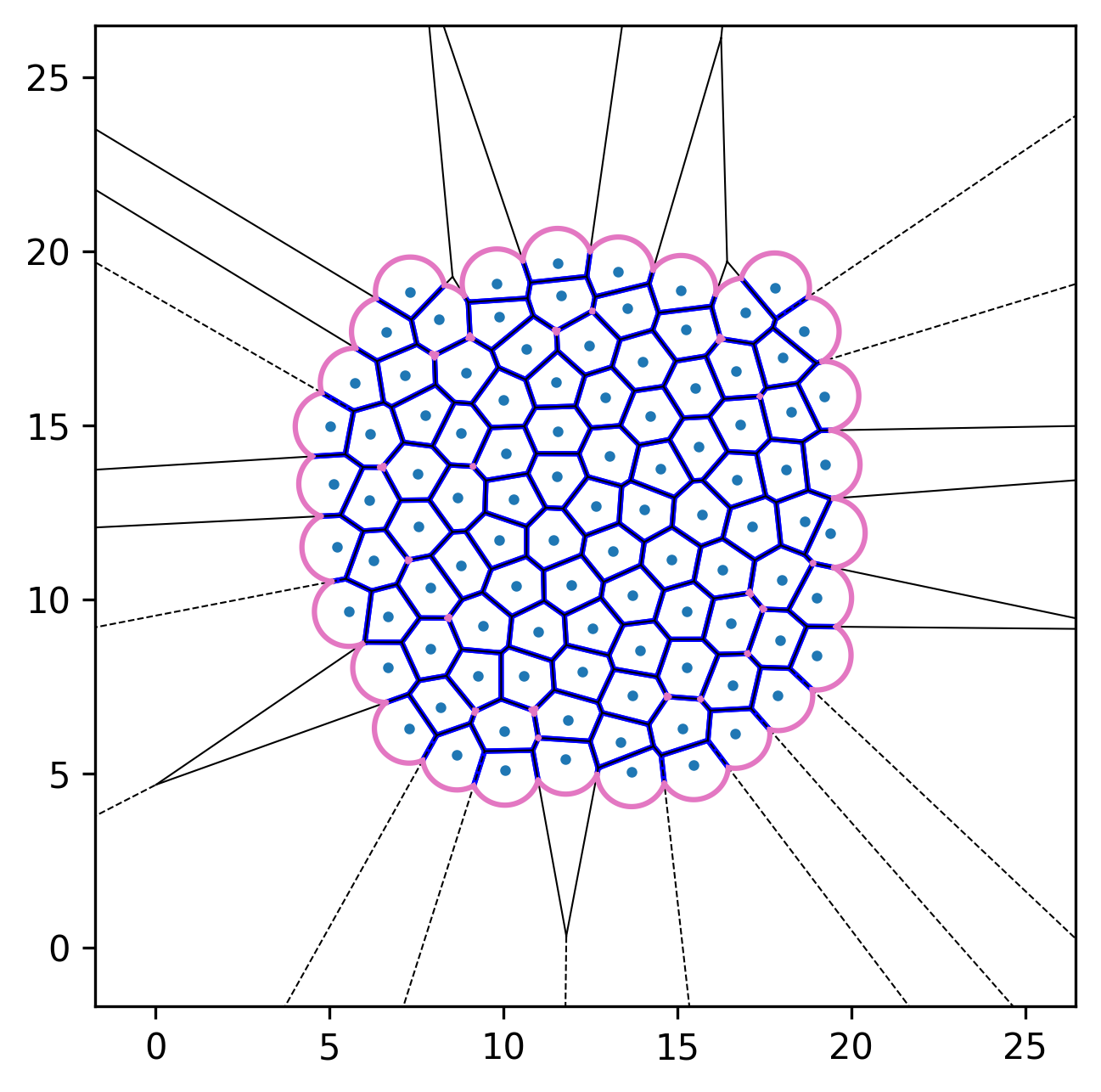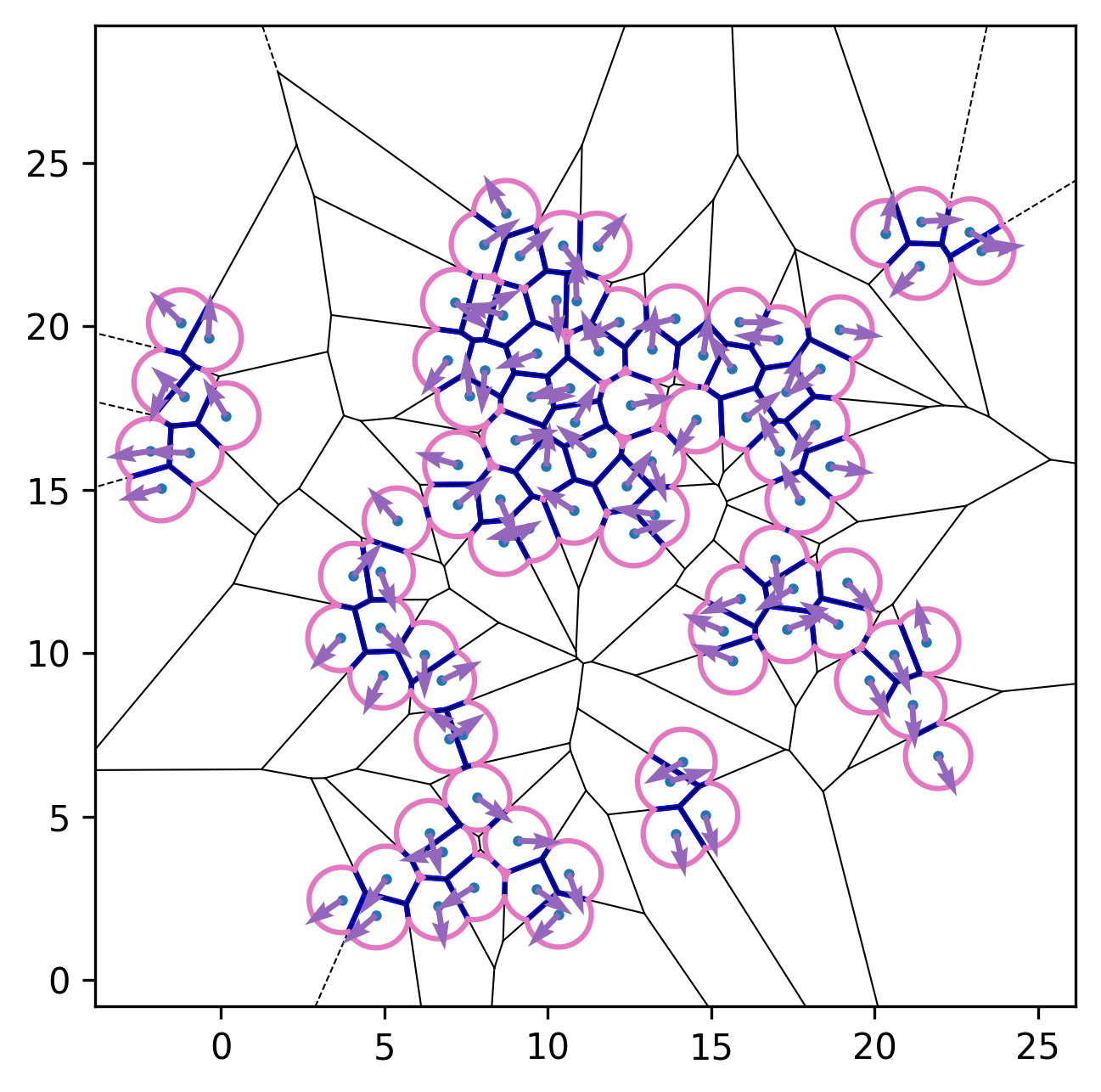• Full documentation on readthedocs or as a single PDF file.

• See CONTRIBUTING.md or the documentation for local development instructions.

• See some important issues for additional context, such as:

  • QhullError when 3+ points are collinear #1 [Closed - see comments]
  • Add customized plotting to examples illustrating access to vertices and edges #5 [Completed in PR #7]
  • Time step dependence of intercellular adhesion in simulations #8 [Closed in PR #9]

• Some releases of this repository are cross-listed on Zenodo:

  

References

[1]	J. Huang, H. Levine, and D. Bi, Bridging the gap between collective motility and epithelial-mesenchymal transitions through the active finite Voronoi model, Soft Matter 19, 9389 (2023).
[2]	E. Teomy, D. A. Kessler, and H. Levine, Confluent and nonconfluent phases in a model of cell tissue, Phys. Rev. E 98, 042418 (2018).
[3]	W. Wang (汪巍) and B. A. Camley, Divergence of detachment forces in the finite-Voronoi model, manuscript in preparation (2026).