Skip to content

数据结构与算法-数组的应用 #31

New issue
New issue
Open
Open
数据结构与算法-数组的应用#31
@wangjing013

Description

@wangjing013
wangjing013
opened on May 16, 2021

数组

  • 什么是数组
  • 数组特性
  • 常见的数组操作
  • 二维数组
  • 真题

什么是数组

数组（Array）是一种线性表数据结构. 它用一组连续的内存空间, 用来存储一组具有相同类型的数据.

数组应该是日常使用最多一种数据结构, 下面通过如下几个方面来了解数组.

数组特性

  • 线性结构
  • 连续的内存空间和相同数据类型(JavaScript中例外)

正由于这两个限制, 它才可以做到随机访问. 凡事有利就有弊, 这两个限制也让数组很多操作变得低效, 比如: 要想在数组中删除、插入一个数据,就需要做很大的搬移操作.

下面了解数组常见操作: 数组创建、添加元素、遍历、删除

常见的数组操作

数组创建

数组创建通常有两种方式:

  • 字面量
  • 通过 new Array() 方式

字面量

const arr = [];

构造函数方式

const arr = new Array();

构造函数 Array 可以接受可选参数:

  • elementN 基于提供元素创建数组(当只给定一个元素时且为数值则等价于 arrayLength)
  • arrayLength 创建给定长度的空数组
const arr = new Array(1,2,3,4);
console.log(arr);

const arr1 = new Array(3);
console.log(arr1);

通常使用字面量的方式即可.

添加元素

const arr = [];
arr[0] = 1; // 通过访问属性方式添加
arr.push(1); // 从尾部添加
arr.unshift(1); // 从头添加
arr.splice(0,0,1); // 支持任意位置

删除元素

const arr = [1,2,3,4];
delete arr[0] // 这种方式并不会改变数组长度, 只是把当前位置内容删除(值为 undefined)

arr.splice(0,1); // 任意位置删除
arr.shift(); // 从头部删除
arr.pop();  // 从尾部删除

通常在删除元素时会触发搬移操作, 这就是为什么数组删除操作在绝大部分情况下是低效率的. 例如 splice 删除指定索引位置的元素，假如从中间删除 或 头部删除时.

通常数组存储数据没有特殊要求的情况下(数组元素有序), 我们是可以通过标记的方式表示数组元素已经被删除, 等到一定情况下再一起删除.

数组遍历

  • for
const arr = [1,2,3,4]
for(let i=0;i<arr.length;i++){
  console.log(arr[i]);
}
  • forEach
const arr = [1,2,3,4]
arr.forEach((item, index, arr)=> {
  console.log(item, index, arr)
})
  • map

map 和 forEach 很像, 其区别在于两者用途不一样, map通常用于对数据进行加工处理, 因为他可以返回一个修改后的数组.

const arr = [1,2,3,4]
arr.map((item, index, arr)=> {
  console.log(item, index, arr)
  return item;
})

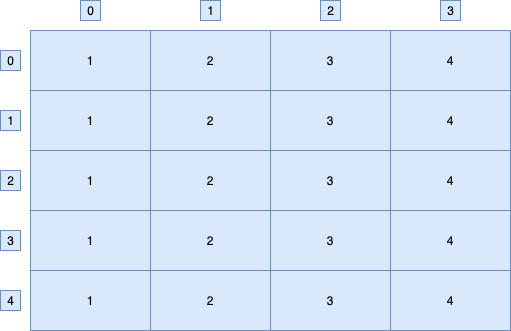
二维数组

通常来说就是数组的嵌套, 结构如下:

const arr = [
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
]

也就是 arr 数组中的元素是数组.

二维数组

二维数组的初始化

fill 的局限性

const arr = (new Array(7)).fill([])
console.log(arr);

输出结果如下:

> arr
(7) [Array(0), Array(0), Array(0), Array(0), Array(0), Array(0), Array(0)]
0: []
1: []
2: []
3: []
4: []
5: []
6: []
length: 7
__proto__: Array(0)

现在修改数组内容:

arr[0][0] = 1;
console.log(arr);

输出结果如下:

> arr
(7) [Array(1), Array(1), Array(1), Array(1), Array(1), Array(1), Array(1)]
0: [1]
1: [1]
2: [1]
3: [1]
4: [1]
5: [1]
6: [1]
length: 7
__proto__: Array(0)

这是什么原因导致, fill 原因传入引用类型时其填充内容就是该引用. 所以这里是我们需要注意的.

通过 for 循环

const arr = [];

for(var i = 0; i< 7;i++){
  arr[i] = []
}

二维数组的访问

同访问一维数组区别不大, 唯一区别在于使用二层循环.

const arr = [
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
  [1,2,3,4],
]
const outerLen = arr.length;
for(let i =0; i< outerLen;i++ ){
  let innerLen = arr[i].length;
  for(let j=0;j< innerLen; j++){
    console.log(arr[i][j]);
  }
}

真题

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标.

先定义一个数组如下:

const nums = [2,7,11,15];
const target = 9;

分析上述题, 其实我们只需要找到 nums[i] + nums[j] = target 然后返回相应的下标[0, 1].

双层循环

最简单的办法就是通过双层循环的方式, 外层记录 i, 内层记录 j, 如下:

const nums = [2, 7, 11, 15];
function twoSum(nums, target) {
  const len = nums.length;
  for (let i = 0; i < len; i++) {
    for (let j = 0; j < len; j++) {
      if (nums[i] + nums[j] == target) {
        return [i, j];
      }
    }
  }
}
console.log(twoSum1(nums, 9))

这中方式怎么样 ? 利用时间复杂度来评估上述代码在当数组数量为 n 时, 其时间复杂度为 n^2.

空间换时间, 可以借助 Map 来实现

const nums = [2, 7, 11, 15];
function twoSum(nums, target) {
  const len = nums.length;
  const map = {};
  for (let i = 0; i < len; i++) {
    let difference = target - nums[i];
    if(map[difference] !== undefined){
      return [map[difference], i];
    }
    map[nums[i]] = i;
  }
}

也可以使用 ES6 中 Map 来完成

// ES6 中 Map
function twoSum(nums, target) {
  const map = new Map();
  const len = nums.length;
  for (let i = 0; i < len; i++) {
    let difference = target - nums[i]
    if (map.has(difference)) {
      return [map.get(difference), i];
    }
    map.set(nums[i], i);
  }
}

强大的双指针

合并两个有序数组

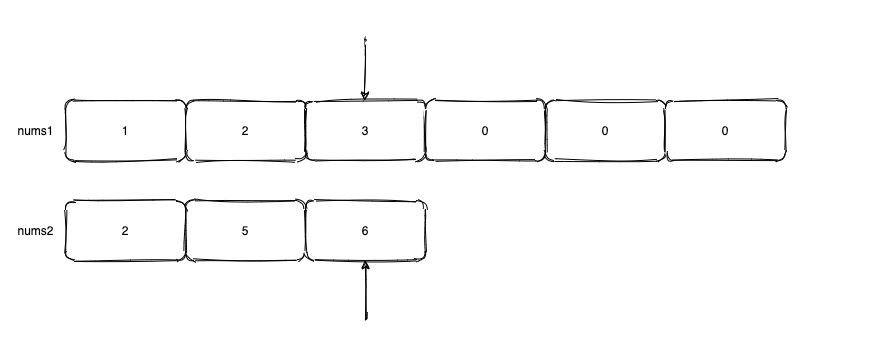
描述: 给你两个有序整数数组 nums1 和 nums2 , 请将 nums2 合并到 nums1 中, 使 nums1 成为一个有序组.

说明: 初始化 nums1 和 nums2 的元素数量分别为 m 和 n.

示例:

// 输入:
nums1 = [1,2,3,0,0,0] m = 3;
nums2 = [2,5,6] n = 3;
// 输出: [ 1, 2, 2, 3, 5, 6 ]

思路分析

标准的解法通过双指针.

  • 定义两个指针，分别指向两个数组的有效部分也就是 m 和 n

double_point_01

  • 指针位置相互比较, 取较大的值往后面补

double_point_02

下面通过代码来实现:

function mergeArr(nums1, m, nums2, n) {
  /**
   * 定义指针
   * p1 表示 nums1 指针, 指向nums1有效位置最后元素位置(对应上图 ``3``)
   * p2 表示 nums2 指针, 指向nums2最后元素位置(对应上图 ``6``)
   * p3 表示 nums1 最后一个元素位置的指针
   */
  let p1 = m - 1;
  let p2 = n - 1;
  let p3 = m + n - 1;

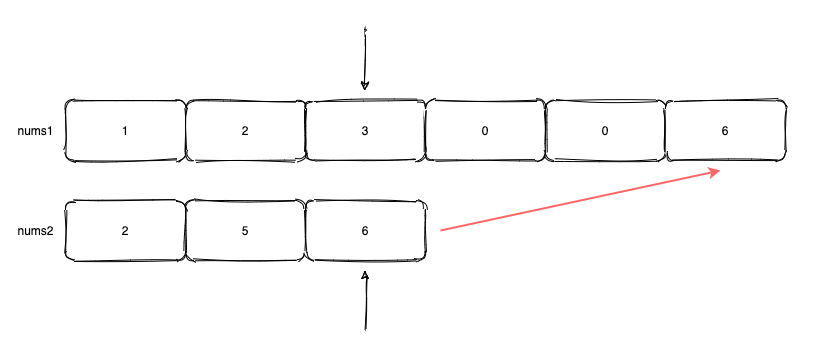
  while (p1 >= 0 && p2 >= 0) {
    if (nums1[p1] < nums2[p2]) {
      nums1[p3] = nums2[p2];
      p2--;
      p3--;
    } else {
      nums1[p3] = nums1[p1];
      p1--;
      p3--;
    }
  }
  /**
   * 特殊处理主要原因: nums1 循环完了，但是 nums2 并没有循环完, 出现这种情况原因有
   * 1. 只有当 nums2 中元素存在比 nums1 中元素小时会出现.
   * 2. nums1 有效元素小于 nums2 中内容.
   */
  while (p2 >= 0) {
    nums1[p3] = nums2[p2];
    p3--;
    p2--
  }
  return nums1
}

三数求和问题

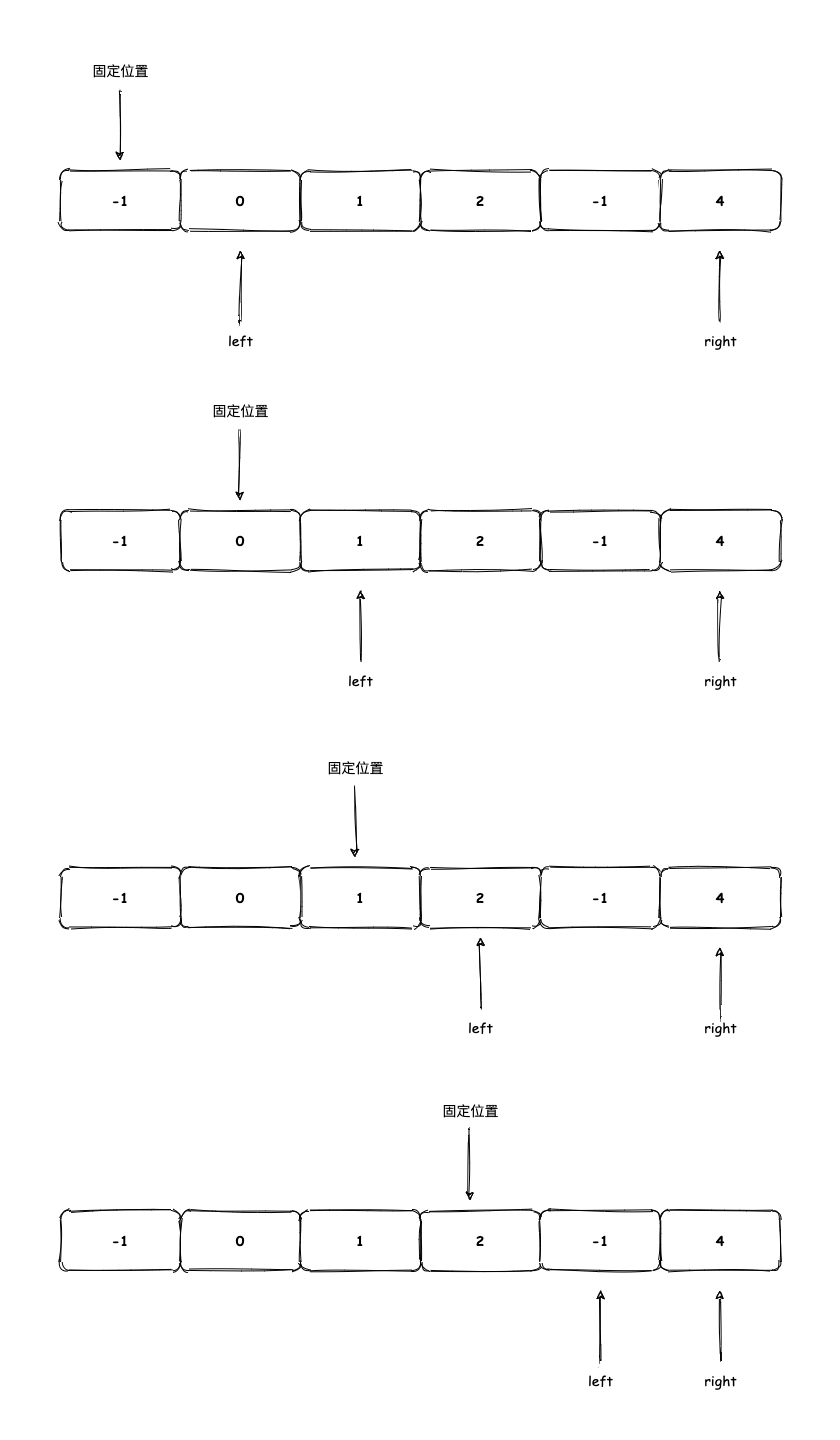
真题描述：给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a, b, c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组.

给定数组 nums = [-1, 0, 1, 2, -1, -4]， 满足要求的三元组集合为： [ [-1, 0, 1], [-1, -1, 2] ]

思路分析

通常想到的办法就是通过三层循环的方式，从时间复杂度来分析看这种方式效率非常低.

继续沿用两数求和的思路, 把求和的问题转变为求差问题 - 固定一个数, 在剩下都数中寻找是否有两个数和这个固定的数相加等于0.

通过一个图描述大概过程:

三数之和

注意 当使用双指针做数组合并、求和时, 首先保证数组是有序的, 这样才能通过双指针来有效缩小查找范围.

下面具体代码实现:

function threeSum(arr) {
  // 内容排序
  arr = arr.sort((a, b) => a - b)
  // 存放有效三元组
  const results = [];

  // 由于左右指针缘故, 我们只需要遍历 arr.length - 2 次数.
  const len = arr.length - 2;
  for (let head = 0; head < len; head++ ){
    // 左指针
    let left = head + 1;
    // 右指针
    let right = arr.length - 1;
    // 防止重复
    if (head > 0 && arr[head] === arr[head - 1]) {
      continue;
    }
    while (left < right) {
      const value = arr[left] + arr[right] + arr[head];
      if (value === 0) {
        results.push([arr[head], arr[left], arr[right]])
        left++;
        right--;

        // 处理左指针重复问题
        while (left < right && arr[left] === arr[left - 1]) {
          left++;
        }

        // 处理右指针重复问题
        while (left < right && arr[right] === arr[right + 1]) {
          right--;
        }
      } else if (value > 0) {
        right--;

        // 处理右指针重复问题
        while (left < right && arr[right] === arr[right + 1]) {
          right--;
        }
      } else {
        left++;
        // 处理左指针重复问题
        while (left < right && arr[left] === arr[left - 1]) {
          left++;
        }
      }
    }
  }
  return results;
}

双指针中的对撞指针法

上述中 left 、right 两个指针从两侧向中间移动，这中特殊的形态称为对撞指针.

通常涉及到 有序 和 数组时, 应该立马想到双指针，当普通的双指针不能满足时, 就可以考虑对撞指针.

其次当数组中不是有序的情况下, 也应该考虑去创建相应的条件(排序).

总结

  • 数组是一种线性结构、有序的
  • 数组常见操作
    • 创建
    • 添加
    • 删除
    • 遍历
  • 数组简单算法题
    • 两数求和
    • 三数求和
  • 从解决思路中引入的概念:
    • 标准双指针法
    • 对撞指针法

通常在实际应用中, 当时间复杂度太大时, 我们可以适当考虑用空间换时间的方式. 反之也成立. 具体根据实际的业务去决定的.

Metadata

Metadata

Assignees

No one assigned

    Labels

    No labels
    No labels

    Projects

    No projects

    Milestone

    No milestone

    Relationships

    None yet

    Development

    No branches or pull requests

    Issue actions