The original is here
- Learning Programming Bitcoin
- a + b, a * b が集合内に存在する = 閉じている
- a + 0 = a となる 0 が集合内に存在する
- この 0 が加法単位元
- a * 1 = a となる 1 が集合内に存在する
- この 1 が乗法単位元
- a + (-a) = 0 となる -a が集合内に存在する
- この -a が加法逆元
- a * a^-1 = 1 となる a^-1 が集合内に存在する
- この a^-1 が乗法逆元
- 体の位数は必ず素数の冪
7 % 3 = 1
- 有限体の加算を +f と表現
- 有限体の減算を -f と表現
位数が19の有限体 => F19 = {0, 1, ... 18}
7 +f 8 = (7 + 8) % 19 = 15
11 -f 9 = (11 - 9) % 19 = 2
- 有限体の加算を *f と表現
5 *f 3 = 5 +f 5 +f 5 = 15 % 19 = 15
7^3 = 343 % 19 = 1
- 有限体の加算を /f と表現
除算は乗算の逆算
通常の数学
- 7 * 8 = 56 は 56 / 8 = 7 を表す
集合体の場合
3 *f 7 = 21 % 19 = 2は2 /f 7 = 3を表す9 *f 5 = 45 % 19 = 7は7 /f 5 = 9を表す
p を素数とし、a を p の倍数でない整数(a と p は互いに素)とするときに、
すなわち、a の p − 1 乗を p で割った余りは 1 であるというもの。
n^(p-1) % p = 1
合同式(mod)の意味とよく使う6つの性質 | 高校数学の美しい物語
y^2 = x^3 + a*x + b
y^2 = x^3 + 7
まず、無限遠点を
とすると、
である。すなわち、
が単位元である。
それ以外の場合、
は、2点
を通る直線とEとの(
および
と異なる)交点の、y座標の符号を反転したものである。すなわち
は以下のようになる。




と、言葉だけで説明するといまいち良く分からないですね。というか無限遠点って何だ。
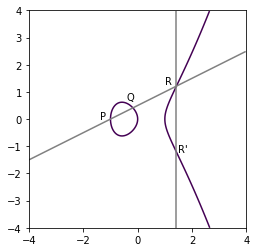
とりあえず無限遠点のことは置いといて、無限遠点じゃない点に関しての加法演算を視覚化してみます。

P と Q を通る直線と楕円曲線の新たな交点の y 座標を反転した点 R' が一意に定まることが分かるでしょうか。
一方で、上図の R と R' のように、x軸に対称な2点に加法演算を適用した場合、直線と楕円曲線は新たな交点を作らないので、楕円曲線上の一意な点を作れません。このような場合に解なしとしてしまうと加算群が作れなくなってしまうので、無限遠点が導入されます。
- 同一性
- 単位元があること
- A + I = Aとなる点Iが存在する
- この点を 無限遠点 と呼ぶ
- 可逆性
- A + (-A) = I
- 可換性
- A + B = B + A
- 結合性
- (A + B) + C = A + (B + C)
2章の楕円曲線は実数。実数が体の1つ。
実数は無数にあるが、有限体と同じような性質を持つ。
F103 で
(
y^2 = x^3 + 7) の曲線で、点(17, 64)が曲線上にあることを証明するには
y^2 = 64^2 % 103 = 79
x^3 + 7 = (17^3 + 7) % 103 = 79

有限体 F61 上の楕円曲線 y2 = x3 − x のアフィン点の集合

有限群 F89 上の楕円曲線 y2 = x3 − x のアフィン点の集合
普通にできる。
F223 で
(
y^2 = x^3 + 7) の曲線上で以下を計算する
- (170,142) + (60,139)
- (47,71) + (17,56)
- (143,98) + (76,66)
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
# (170,142) + (60,139)
x1 = FieldElement(num=170, prime=prime)
y1 = FieldElement(num=142, prime=prime)
x2 = FieldElement(num=60, prime=prime)
y2 = FieldElement(num=139, prime=prime)
p1 = Point(x1, y1, a, b)
p2 = Point(x2, y2, a, b)
print(p1+p2) # => Point(220,181)_0_7 FieldElement(223)
# (47,71) + (17,56)
x1 = FieldElement(num=47, prime=prime)
y1 = FieldElement(num=71, prime=prime)
x2 = FieldElement(num=17, prime=prime)
y2 = FieldElement(num=56, prime=prime)
p1 = Point(x1, y1, a, b)
p2 = Point(x2, y2, a, b)
print(p1+p2) # => Point(215,68)_0_7 FieldElement(223)
# (143,98) + (76,66)
x1 = FieldElement(num=143, prime=prime)
y1 = FieldElement(num=98, prime=prime)
x2 = FieldElement(num=76, prime=prime)
y2 = FieldElement(num=66, prime=prime)
p1 = Point(x1, y1, a, b)
p2 = Point(x2, y2, a, b)
print(p1+p2) # => Point(47,71)_0_7 FieldElement(223)同じ点の加算ができる。
(170, 142) + (170, 142) = 2 * (170, 142)
結合性がある。
2 * (170, 142) + (170, 142) = 3 * (170, 142)
楕円曲線上の点と点を掛けるのではなく、点に整数(スカラー)を掛けることに注意。
スカラー倍算の特性の一つに、計算をせず予測することが非常に難しいという点がある。
キャラクターの一歩が P だとします.原点から 2 歩進むと 2P の位置にいます.どんどん進んで端に到達すると逆から出てきます.10 歩でも 100 歩でも 10100 歩でも進めます.そして歩いて到達した位置 10P や 100P,10100P は容易に求められます.
さて,移動していたキャラクターはうっかり何歩歩いていたか忘れてしまいました.現在地と自分の一歩から何歩歩いたのか知りたいのです.実はこれはとても難しいことが知られています.一歩 P が決まっているときに
歩数 n から現在地 nP を求められる ↭ 現在地 nP から n を求められない
有限体のときと同じく,この非対称性が重要です.
「P, nP が与えられたときに n を求めよ.」
という問題を楕円離散対数問題(ECDLP : Elliptic Curve DLP)といいます.
点Gを無限遠点になるまでスカラー倍数する
n*G = 0のとき {G, 2G, 3G, ... nG}
この集合を群と呼ぶ。この集合は n が有限のため、有限群(有限巡回群)になる。
F223で (47,71) のスカラー倍算をしていく。
from ecc import FieldElement, Point
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
x = FieldElement(47, prime)
y = FieldElement(71, prime)
p = Point(x, y, a, b)
for s in range(1,21):
result = s*p
print('{}*(47,71)=({},{})'.format(s,result.x.num,result.y.num))1*(47,71)=(47,71)
2*(47,71)=(36,111)
3*(47,71)=(15,137)
4*(47,71)=(194,51)
5*(47,71)=(126,96)
6*(47,71)=(139,137)
7*(47,71)=(92,47)
8*(47,71)=(116,55)
9*(47,71)=(69,86)
10*(47,71)=(154,150)
11*(47,71)=(154,73)
12*(47,71)=(69,137)
13*(47,71)=(116,168)
14*(47,71)=(92,176)
15*(47,71)=(139,86)
16*(47,71)=(126,127)
17*(47,71)=(194,172)
18*(47,71)=(15,86)
19*(47,71)=(36,112)
20*(47,71)=(47,152)
21*(47,71)は無限遠点になり、22*(47,71) = (47,71)となる。
log2(n)回のループで乗算が実行可能になる。
def rmul(self, coefficient):
coef = coefficient
current = self # <1>
result = 0 # <2>
print(bin(coef), current, result)
while coef:
if coef & 1: # <3>
result += current
current += current # <4>
coef >>= 1 # <5>
print(bin(coef), current, result)
return result
print(rmul(10,11))0b1011 10 0
0b101 20 10
0b10 40 30
0b1 80 30
0b0 160 110
110
有限体上の楕円曲線から生成元となる点を取り出すと、有限巡回群を生成できる。
体とは異なり、群にある演算は点の加算のみ。
群には、閉包、可逆性、可換性、結合性などの特性もある。
- 同一性
- 単位元があること
- 0 + A = Aとなる点Iが存在する
- この点を 無限遠点 と呼ぶ
- 閉包
- aG + bG = (a + b)G
- 可逆性
- aGが群にある場合、(n - a)Gも群にある
- aG + (n - a)G = (a + n -a) = nG = 0
- 可換性
- A + B = B + A
- 結合性
- (A + B) + C = A + (B + C)
- 曲線
- 有限体の素数p
p = 2**256 - 2**32 - 977
- 生成点Gのx, y座標
gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
- Gにより生成される群の位数
0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
p = 2**256 - 2**32 - 977
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141P = eG
PはeとGの値がわかればすぐに計算できる。eの値はPとGがわかっていても簡単には計算できない。
一般に eを秘密鍵、Pを公開鍵と呼ぶ。
秘密鍵は256bitの数で、公開鍵は座標 (x, y) で、xとyはそれぞれ256bitの数。
やりたいこと
- 秘密鍵の数値を知っていることを、秘密鍵の数値を明らかにせずに証明したい
署名アルゴリズム
- 楕円曲線デジタル署名アルゴリズム (Elliptic Curve Digital Signature Algorithm)
秘密鍵は、以下を満たす e。
eG = P
Pが公開鍵で、eは秘密鍵。
ランダムな256bitの数字 k で↓を計算する。
kG = R
Rのx座標に注目し、これを r とする。
次の方程式が離散対数問題と等価。
uG + vP = kG
u, v は 0 ではない値を署名者が選ぶ。G と P は既知。
uG + vP = kG
vP = (k - u)G
v != 0 であるため、vで割る
P = ((k - u)/v)G
すなわち e = (k-u)/v となるので、これを満たす u, v の組み合わせを選ぶ。
eを知らない場合、e = (k-u)/vになるまでいろいろ試す必要がある。
離散対数問題は難しいので、e, u, vは定めた人が知っていると考えられる。
署名ハッシュを z とする。 r と s が署名
u = z/s, v = r/s
これを解くために s の値を求める。
uG + vP = R = kG
eG = P なので
uG + veG = kG
u + ve = k
u = z/s, v = r/s なので
z/s + re/s = k
(z + re) / s = k
s = (z + re) / k
この式が署名アルゴリズムの基礎。
k が明かされると、いろいろ無駄になるので、k には完全にランダムな値を使う。
署名する対象は固定長の値で 32 byte の値。
署名する対象は G の係数になる。
ドキュメントを hash256 で 32 byte にする。sha256 を2回繰り返すことで、32byte になることが保証される。これが署名ハッシュ zになる。
検証する署名には (r, s) の2つがある。
- r は R の x座標
- s は
s = (z + re) / k
知っている値
- e (秘密鍵, P = eG)
- k (ランダムな値, kG = R)
- z (署名ハッシュ)
u, v を定義して、 R = uG + vP を次のように構成する
- u = z / s
- v = r / s
こんなふうに展開できる。
uG + vP = (z/s)G + (r/s)P = (z/s)G + (re/s)G = ((z+re)/s)G
s = (z + re) / K なので
uG + vP = ((z+re)/s)G = ((z+re)/(z+re)/k)G = R
検証手順
- 署名を (r,s) 、署名対象のハッシュを z、署名者の公開鍵を P とする
- u = z/s, v = r/s を計算する
- uG + vP = R を計算する
- R の x座標と r が同じ値なら署名は有効
署名の手順
- z(署名ハッシュ) が与えられており、eG = P を満たす e(秘密鍵) がわかっているとする
- ランダムに k を選ぶ
- R = kG と r (Rのx座標)を算出する
- s = (z + re)/k を算出する
- 署名は (r, s) となる
P(公開鍵)は、検証したい相手に転送する。z は検証者が必ず知る必要がある。z 算出され、P は署名とともに送信する。
SEC(Standards for Efficient Cryptography)
点 P = (x, y) に対する非圧縮SECフォーマットの生成
- プレフィクスバイトから始める。 0x04
- 次に、32 byteのビッグエンディアン整数としてx座標を追加
- 次に、32 byteのビッグエンディアン整数としてy座標を追加
- ビッグエンディアン
- 8 bitなので、基数は256
- 大きいほうから始まる
- 500 => 01f4 (500 = 1 * 256 + 244 = 0100 + 00f4 = 01f4)
- リトルエンディアン
- 8 bitなので、基数は256
- 小さいほうから始まる
- 500 => f401 (500 = 244 + 1 * 256 = 00f4 + 0100 = f401)
楕円曲線は y^2 の項があるので、任意のx座標に対して、最大2つのy座標がある。
y^2 = x^3 + a*x + b
上記を満たす任意の (x, y) では (x, -y) も式を満たす。
有限体では -y % p = (p - y) % p となる。P は位数なので2以上の素数なので、必ず奇数になる。
y が奇数の場合、 p - y は偶数になる。つまり y と p - y は一方が奇数、一方が偶数になる。これを利用して非圧縮SECフォーマットを圧縮できる。x座標と、y座標が偶数か奇数かを示せばよい。y座標をシングルバイトに圧縮する(偶数か奇数か)ため、これを圧縮SECフォーマットと呼ぶ。
点 P = (x, y) に対する圧縮SECフォーマットの生成
- プレフィクスバイトから始める
- y が偶数の場合は 0x02
- y が奇数の場合は 0x03
- 次に32バイトのビッグエンディアン整数としてx座標を追加する
数学的に表すと、以下のようになる。
v から w^2 = v となるような w を求めよ。
位数 p が p % 4 = 3 を満たす場合、簡単に解ける。
P % 4 = 3 => (p + 1) % 4 = 0
つまり (P + 1) / 4 は整数になる。
フェルマーの小定理を使う
w^(p-1) % p = 1
w^2 = v
w^2 = w^2 * 1 = w^2 * w^(p-1) = w^(p+1)
結果が整数になる (p + 1) / 4 を次のように用いる。
w = w^{(p+1)/2} = w^{2(p+1)/4} = (w^{2})^{(p+1)/4} = v^{(p+1)/4}
よって、平方根を求める式はこうなる
w^2 = v かつ p%4 = 3 の場合、 w = v^(p+1)/4
secp256k1 で用いられる p P%4 == 3 あんおで以下の式が成り立つ。
w = v^(p+1)/4
この式であり得る2つの w の値のうち1つが求められ、もう1つは p - w になる。
- 非圧縮フォーマットは普通に確認する
- 圧縮フォーマットは最初のバイトでy座標が偶数か奇数かわかる
- 楕円曲線の式の右辺の平方根を計算し y の値を求める
- 偶数、奇数を判断して、正しい点を返す
DER(Distinguished Encoding Rules)
DER署名フォーマット
- 0x30 ではじめる
- 署名の残りの長さ (0x44 or 0x45)
- マーカーバイト 0x20
- rをビッグエンディアンの整数としてエンコード。rの戦闘が0x80以上の時は先頭に0x00をつける
- マーカーバイト 0x20
- sをビッグエンディアンの整数としてエンコード。rの戦闘が0x80以上の時は先頭に0x00をつける
Base58は、データを58種類の印字可能な英数字のみを用いて、それ以外の文字を扱うことの出来ない通信環境にてマルチバイト文字やバイナリデータを扱うためのエンコード方式である。Base64に似ているが、英数字以外の文字や印刷した場合に違いのわかりにくい文字を排するような変更がなされている。これは生身の人間であるユーザーが手動でデータを入力したり、視覚的な情報源から目でコピーすることを想定しているほか、ダブルクリック一発で文字列すべてを選択し楽にコピー&ペーストができるように設計されているためである。
Base58ではBase64から数字の0と大文字のO、大文字のIと小文字のlの英数字といった区別しづらい文字や、英数字以外の特殊文字である+(プラス)/(スラッシュ)を取り除いた文字セットで表現される。Base58はエンコード時のデータの分割単位が58と2の冪の数ではないため、Base64のように元データをビット毎に分割することができない。このため大きいバイナリデータをエンコードすることは不得手であり、専ら大きな整数をエンコードするのに用いられる。 後述の例のように文字セットの並び順の正しい規定が存在せず個別の実装に依存しており、同じ"Base58"という名前でも複数のフォーマットが存在する。派生フォーマットとして文字セットから更に数字の1と小文字のoの2文字を取り除いたBase56というものも存在する。
Base58Checkは最初と最後の数文字でそれぞれデータ種別とエラー検出符号を付加するBase58エンコードフォーマットであり、ビットコインのアドレスはこの形式をとっている。
圧縮SECは 264byte と長い。アドレスを短くして安全性を高めるために ripend160 ハッシュを使う。 SECフォーマットを直接使わないことで、アドレスを 33byte から 20byte にできる。
ビットコインアドレスの作成方法
- メインネットアドレスは先頭を 0x00、テストネットは 0x60 で開始
- SECフォーマットを取り出し、sha256操作とripend160ハッシュ操作を行う
- これを hash160 操作と呼ぶ
- 1と2を結合する
- 3に hash256 を行い最初の4byteを取得
- チェックサム
- 3と4を結合して、Base58でエンコードする
WIFの作成方法
- メインネットの秘密鍵は 0x80、テストネットの秘密鍵は 0xef のプレフィクス
- 秘密鍵を32byteのビッグエンディアンでエンコードする
- 公開鍵アドレスのSECフォーマットが圧縮形式の場合は、末尾に 0x01 を追加
- 1, 2, 3 の順に結合
- 4 に hash256 して最初の 4byte を取得
- 4, 5を結合させて、Base58にエンコード
トランザクションは4つのコンポーネントで構成される
- Version
- Inputs
- Outputs
- Locktime
トランザクションのバージョンは通常 1
01000000 でリトルエンディアンの整数
ビットコインのインプットは、前のトランザクションのアウトプット。インプットは自分の所有するビットコインを示す。
各インプットには以下が含まれる。
- 前に受け取ったビットコインへの参照
- 支払う本人のビットコインであるという証明
- ECDSAを用いる
インプットは複数あることもある。インプット数は varint(可変長整数)で表現する。
インプットの各フィールド
- Previous transaction ID
- 前のトランザクションのhash256
- 32 byte, リトルエンディアン
- Previous transaction index
- どのアウトプットで支払うかを示すインデックス
- 4 byte, リトルエンディアン
- ScriptSig
- varint
- 6章で詳しく取り上げる
- Sequence
- 高頻度トレードで使いたかったみたい
- よくわからない
ビットコインの送信先を定義する。トランザクションは1つ以上のアウトプットを持つ。
アウトプットには2つのフィールドがある
- amount
- satoshi単位のビットコインのamount
- 8 byte, リトルエンディアンでシリアライズ
- ScriptPubKey
- varint
ロックタイムはトランザクションを遅延させる方法。
ロックタイムが 500,000,000 以上の場合、Unixタイムスタンプ。未満の場合はブロックナンバー。 指定されたUnix時間 or ブロックの高さに到達するまで署名はできるけど、支払いには使えない。
- シリアライズされた 4byte のリトルエンディアン
よくわからない
インプットの合計から、アウトプットの合計を引いた額
インプットにはamountがないので、探さなくてはいけない。UTXO(unspent transaction output)セットへのアクセスが必要になる。
ロックする => ビットコインをエンティティに与える アンロックする => これまでに受け取ったビットコインを支払う
Scriptはチューリング完全ではなく、ループ処理はない。
トランザクションはビットコインをロッキングスクリプトに割り当てる。ロッキングスクリプトはScriptPubKeyフィールドで指定されている。これはお金を預けたロックボックスのようなもの。
ロックボックスはScriptSigフィールドでアンロックできる。
- Scriptは一度に1つのコマンドを実行する
- コマンドはスタック上の要素を操作する
- コマンドにはエレメントとオペレーションがある
エレメントとはデータのことで、典型的なエレメントはDER署名やSEC公開鍵など。技術的にはエレメントを処理することは、そのエレメントをスタックにプッシュすることを指す。
オペレーションはデータに対し何らかの操作をする。
スタックの先頭にエレメントを複製し、新しく生成したエレメントをスタックにプッシュする。
スタックの先頭要素に sha256, ripemd160 の順にハッシュ関数を適用し、生成された新たなエレメントをスタックにプッシュする。
OP_CHECKSIGはスタックからpubkeyとsignatureをポップし、その署名が有効か確認する。有効な場合は1を、無効な場合は0をスタックにプッシュする
Scriptオブジェクトは評価が必要なコマンドのセットを表す。
スクリプトを評価するには、ScriptPubKeyとScriptSigの各フィールドを連結する必要がある。
対応するScriptPubKeyとScriptSigは異なるトランザクションに存在する。
- ロックボックスはビットコインを受け取るトランザクションに
- アンロックするスクリプトはビットコインを支払うトランザクションに
ScriptSigがScriptPubKeyをアンロックするので、連結する必要がある。
ScriptSigとScriptPubKeyからコマンドを取り出し、両者を連結する。ScriptSigからのコマンドは、ScriptPubKeyからの全てのコマンドのうえに配置する。処理するコマンドがなくなるまで1つずつ処理されていく。
さまざまな種類の標準的なスクリプトがある。
- p2pk: Pay-to-pubkey
- p2pkh: Pay-to-pubkey-hash
- p2sh: Pay-to-script-hash
- p2wpkh: Pay-to-witness-pubkey-hash
- p2wsh: Pay-to-witness-script-hash
スタックエレメントは0や1などの数字の場合もあれば、DER署名、SEC公開鍵などの場合もあるが、内部的にはすべてバイトになる。特定のオプコード向け数値と解釈されるものもある。
ノードが主に確認するすること
- そのトランザクションのインプットを過去に支払っていないこと
- そのインプットの合計額がアウトプットの合計額以上になっていること
- ScriptSigが前のScriptPubKeyのアンロックに成功していること
UTXOセットを検索する。
インプットには額を表すフィールドがないので、ブロックチェーンを検索する。
フィーの計算を行い、フィーがマイナスではないこと確認する。
ECDSA署名アルゴリズムは、公開鍵 P、署名ハッシュ z、署名 (r, s)が必要。
各インプットは前のトランザクションアウトプットを指し、そこにScriptPubKeyがある。
インプットがさしているScriptPubKeyを取り出して、空になっているScriptSigに入れる。
ハッシュタイプを付加する。ほとんどのトランザクションはSIGHASH_ALLで署名されている。SIGHASH_ALLの場合、最終的なトランザクションのアウトプットは署名対象とすべて一致しなくてはならない。SIGHASH_ALLに対応する整数は1で、リトルエンディアンで4バイトでエンコードする。
この変更されたトランザクションのhash256はビッグエンディアン整数として解釈され z となる。ScriptSigからSECフォーマットの公開鍵と、DERフォーマットの署名を取り出して、署名を検証できる。
作成するトランザクションは以下のようなことが必要。
- インプットの合計がアウトプットの合計以上になる
- ScriptPubKeyと連結した場合に有効になるScriptSigが必要
- UTXOセットからのアウトプットのうち、ScriptPubKeyを自分でロック会場できるもの
- 受け取ったアウトプット
署名する必要のあるインプットが複数ある場合、インプットごとに正しい秘密鍵で生成した署名が必要。
- 署名は実際にはDER署名とハッシュタイプの組み合わせで、この場合はSIGHASH_ALL
- p2pkhのScriptSigには署名とSECフォーマットの公開鍵の2つのエレメントある
これまで扱ってきたのは、単一鍵のトランザクション、つまりインプットごとに単一の秘密鍵のみを使うトランザクションだった。単一の鍵を紛失するとリスクが大きい。そのための解決方法がマルチシグ。
トランザクションアウトプットは長いScriptPubKeyのままなので "Bere" Multsigと呼ばれる。複数の署名が必要となるアウトプットを持つトランザクションを作成する最初の試み。
OP_CHECKMULTISIGは、スタックから多数の要素をポップし、必要な数の署名が、トランザクションインプットに対して有効か否かを返す。
ベアマルチシグにはいくつかの問題がある。
- ScriptPubKeyに複数の公開鍵があるので長くなる
- アウトプットが通常のp2pkhアウトプットの5-20倍と長い
- ScriptPubKeyが非常に大きくなる可能性があるため、悪用される可能性がある
Pay-to-script-hash(p2sh)は長いアドレス/ScriptPubKey問題を解決する一般的な方法。Scriptコマンドの播種を取得し、後でハッシュかする前のScriptコマンドを明らかにする。
RedeemScriptはスクリプトのハッシュを取得して、スクリプトを引き替えたいときに利用しやすいように保持する。RedeemScriptのハッシュはScriptPubKeyとして配置する。
RedeemScriptをhash160した値と、hashを比較する。
ブロックは各トランザクションを整列させる手段。
10分ごとにまとまった単位でトランザクションの集まりを決済することで、ビットコインは妥協点を見つけている。トランザクションの集まりがブロック。
コインベースは各ブロックの最初に要求されるトランザクションで、ビットコインの発生を可能にする唯一のトランザクション。
コインベーストランザクションのアウトプットはマイニングをした人によって保持され、通常、ブロック内のほかのトランザクションすべての手数料と、ブロック報酬(リワード)が含まれる。
ブロックはトランザクションの集まり。ブロックヘッダーはブロックに含まれるトランザクションのメタデータ。
- Version
- Previous block
- すべてのブロックは前のブロックを指している必要がある
- Merkle root
- 順番に並んだすべてのトランザクションを32バイトハッシュにエンコーディングする
- Timestamp
- Bits
- Proof-of-Workに必要な値をエンコーディングするフィールド
- Nonce
- number used only once 1度だけ使われる数値
- マイナーがProof-of-Workを探す際に変更される
Proof-of-Workを見つけることで、マイナーはブロックをブロックチェーンに加える権利を得る。
- ブロックヘッダーのhash256が小さい値になるものを探す
- hash256(sha256を2回)した値が小さい値になる可能性は低い
- ブロックヘッダーのhash256がターゲットを下回る値になるブロックヘッダーを探す
nonceを自由に変えることで、ブロックヘッダーのハッシュを変える。nonceフィールドを使い切ったときは、コインベーストランザクションを変更する。これによりマークるルートが変更され、あたらしいnonce領域が与えられる。
ターゲットはビットフィールドから直接計算される256ビットの数値。
ビットフィールドは指数(exponent)と係数(coefficient)から構成されている。
- target = coefficient * 256^(exponent-3)
ターゲットは小さい値になる。
ターゲットは人間が理解するのは困難。ターゲットを比較しやすくために生まれたがのディフィカルティ。比較を容易にするため、ディフィカルティがターゲットに反比例する。
- difficulty = 0xffff * 256^(0x1d-3) / target
ビットコインでは2016ブロックの各グループをディフィカルティ調整期間と呼ぶ。調整期間の終わりにターゲットが調整される。
time_differential = 調整期間の最後のブロックのタイムスタンプ - 調整期間の最初のブロックのタイムスタンプ
new_target = time_differential / 2週間
- time_differentialは8週間を超える場合、8週間になる
- time_differentialは 3.5日未満の場合、3.5日になる
ブロック生成時間が1ブロック平均10分に収束するようになっている。
最初の4バイトは常に同じでネットワークマジックと呼ばれる。通信は非同期で断続的なることもあるため、マジックバイトはネットワークプログラミングでは一般的。通信が中断されたときに再開すべき場所の目印となる。またネットワークの識別にも役立つ。
次の12バイトはコマンドフィールドで、ペイロードが実際に伝達する内容の説明。コマンドの一覧は以下に記載されている。
次の4バイトはペイロードの長さをリトルエンディアンで示したもの
次の4バイトはチェックサム。ペイロードのhash256の先頭4バイト。ネットワークプロトコルのチェックサムは通常エラー訂正機能があるが、hash256にはそれがない。
各コマンドには、それぞれのペイロードの仕様がある。
versionのペイロードの仕様は以下で定義されている。
ノードが通信を確立する方法。
- AがBに接続するために、versionメッセージを送信
- Bはversionメッセージを受信し、varackメッセージで応答し、自身のversionメッセージを送信
- Aはversionメッセージとvarackメッセージを受信し、varackメッセージを送信
- Bはverackメッセージを受信し、通信を継続する
どのノードも初めてネットワークに接続する際、取得して検証すべき最も重要なデータはブロックヘッダー。
フルノードの場合、ブロックヘッダーをダウンロードすると複数のノードに完全なブロックを非同期に要求してブロックのダウンロードを並列化できる。
軽量クライアントの場合、ヘッダーをダウンロードすることで、各ブロックのProof-of-Workを検証できる。
ブロックヘッダーを取得するコマンドはgetheaders。取得できるヘッダーの最大数は2000で、概ね1つのディフィカルティ調整期間(2016)になる。
相手ノードからヘッダーを受信する。相手ノードはheadersコマンドを送り返す。
ヘッダー数は1から2000までの数値。
各ブロックヘッダーは80バイト。
次にトランザクション数が続くが、headersメッセージの数は常に0。トランザクションではなくheaderを要求したため。
- Proof-of-Workの確認
- ブロックヘッダーのhash256を計算して、この値がターゲットより小さいことを確認
- 現在のブロックが前のブロックの次にあることを確認
- ブロックヘッダーのPrevious Blockの確認
- ビット/ターゲット/ディフィカルティが前のエポックのでの計算に基づいていることを確認
- エポックの終わりに次のビット/ターゲット/ディフィカルティを計算
- エポックの終わりにエポックのビットの計算用に、エポックの最初のブロックを保存
マークルルートとマークルツリーで包含証明を行いたい。
どのウォレットにも2つのシナリオがある。
- 誰かに支払う
- 誰かから支払いを受ける
トランザクションが十分に深いブロックに取り込まれたら、支払いに対する商品やサービスが提供される。
完全なブロックチェーンを持っていれば、トランザクションが十分に深いブロックにあることを簡単に確認できる。
完全なブロックチェーンを持っていない場合の確認の仕方を紹介する。
SVPは便利だが、ほとんどの軽量ウォレットではSVPを使用していない。SPVの主な欠点は対象トランザクションについての何かを接続先ノードが知っていること。SPVを使用するとプライバシーが失われれる。この点については12章で扱う。
ハッシュ木はノードにハッシュ値を持つ二分木であり、葉の部分にはデータブロック(ファイルや、ファイルを分割したものなど)のハッシュ値が入っている。葉より上位のノードにはそれぞれの子ノードのハッシュ値が入っている。例えば、上図においてhash 0には、hash 0-0とhash 0-1とを結合した結果のハッシュ値が入っている。つまり、hash 0 = hash(hash 0-0 || hash 0-1)となっている(ここで||は文字列結合の意味)。
- H = ハッシュ関数
- P = Parent hash
- L = Left hash
- R = Right hash
P = H(L||R)
||は連結を示す
3つ以上のハッシュの順序付きリストが与えられると、各ペアの親ハッシュが計算できるようになる。これをマークルペアレントレベルと呼ぶ。ハッシュの個数が奇数の場合、最後のアイテムを複製する。
ハッシュの個数が1つになるまで繰り返しマークルペアレントレベルを計算する。
軽量クライアントがHKとHNを持っているとする。フルノードは青色のボックスのハッシュを全て送信することで、包含関係を証明できる。
軽量クライアントは点線のボックスのハッシュを計算する。計算からマークルルートを取得したら、Proof-of-Workが検証済みのブロックヘッダーのマークルートと比較してチェックできる。
フルノードが包含証明を送信するとき2つの情報を含める必要がある。
- マークルツリーの構造
- マークルツリーのどの位置にどのハッシュがあるか
これらの情報があると、軽量クライアントはマークルツリーを部分的に再構築でき、方眼証明を検証できる。
merkleblockコマンドは、対象のトランザクションがマークルツリーにあることを検証するために必要なすべての情報を送信する。
軽量クライアントはフルノードにアドレス(ScriptPubKey)を伝えることができる。フルノードはこれらのアドレスに関連するトランザクションをチェックできるが、軽量クライアントのプライバシーを危険にさらすことになる。
解決策の一つは、対象となるすべてのトランザクションのスーパーセットを作成するのに十分な情報を軽量クライアントがフルノードに伝えること。このスーパーセットを作成するにはブルームフィルターを使用する
空間効率の良い確率的データ構造であり、あるデータが集合の要素である(集合に含まれている)かどうかの判定に使われる。ただし判定は正確ではなくて、含まれていないのに含まれていると誤って判定すること偽陽性(false positive)の可能性がある。しかし含まれているものを含まれていないと誤判定すること偽陰性(false negative)はない。なお集合に要素を追加することはできるが、集合から要素を削除することはできない(ただし、拡張をした counting filter であれば削除もできる)。集合に要素を追加していくにつれて偽陽性の可能性は増す。
ネットワーク通信におけるブルームフィルターを規定する。
- ビットフィールドのサイズはバイトで指定され、必要に応じて切り上げられる
- ハッシュ関数の数
- 該当アイテムが多すぎる場合に、微調整できる昨日
- 対象のアイテムにブルームフィルターを実行した結果のビットフィールド
軽量クライアントがブルームフィルターを作成したら、フルノードに詳細を伝える必要がある。コマンドはfilterloadになる。
軽量クライアントがフルノードからもらいたいデータのタイプはフィルター済みブロック。マークるブロック形式でブルームフィルターを通過するトランザクションを要求する。つまり軽量クライアントは対象のトランザクションがブルームフィルターに一致するマークるブロックを要求できる。
フルノードにブルームフィルターを読み込ませた軽量クライアントは対象トランザクションが特定のブロックに含まれていることを証明するのに必要なすべての情報を取得する。
SegitはSegregated Witnessの略で、2017年8月にアクティベートされたソフトフォーク。以下のような変更が取り入れられている。
- ブロックサイズの増加
- トランザクションマリアビリティの解消
- 明確なアップグレードパスのためのSegwitバージョン管理
- 二次ハッシュの修正
- オフラインウォレット手数料計算のセキュリティ
p2pkhからの主な変更点は、ScriptSigのデータがwitnessフィールドに移動したこと。これはトランザクションのマリアビリティを解消するため。
トランザクションマリアビリティとは、トランザクションの意味を変えずに、トランザクションIDを変更すること。
トランザクションのマリアビリティが問題になるのは、トランザクションIDがトランザクション全体から計算されることにある。トランザクションのほとんどのフィールドはトランザクションの署名を無効にしないと変更できないため、これらのフィールドは問題にならない。
署名を無効にすることなく操作できるフィールドはScriptSigフィールド。ScriptSigは署名ハッシュを作成する前に空にされるため、署名を無効にすることなく変更できる。
トランザクションがブロックチェーンにはいるとトランザクションIDは固定される。しかしLightning Networkの基本単位となるペイメントチャネルでは、ファンドトランザクションがブロックチェーンに追加されるより前に作成される従属するトランザクションが存在する。
トランザクションのマリアビリティはScriptSigフィールドを空にして、IDの計算に使用されない別のフィールド、witnessフィールドにデータを配置することで修正される。
p2wpkh TransactionsにはSegwit marker、Segwit flag、witnessなどが追加されている。
ScriptSigは空で、ScriptPubKeyはOP_Oと20バイトのハッシュ。
OP_Oと20バイトのハッシュの場合、特別なルールが発動する。これは古いノードの場合も有効なスクリプトとみなされる。このシーケンスが検出されるとwitnessフィールドを読み込む。
p2wpkhの残りの処理はp2pkhの処理と同じで、署名が有効な場合はスタックに1が残った状態となる。
これはSegwitバージョン0の特別なルールで、バージョン1は完全に異なる処理パスを持つことができる。
p2wpkhは優れているが、古いウォレットはp2wpkhのScriptPubKeyに送金できない。Segwitの広報互換性を保つため、p2shでp2wpkをラップして対応している。
p2wpkhは主要なユースケースに対応するが、より複雑なスクリプトを利用したい場合、柔軟性の高いものが必要になる。
p2wpkhと同様に特別なシーケンスを認識するとwitnessフィールドを参照する。
witnessの最後の項目はWitnessScriptと呼ばれる。WitnessScriptのsha256が、ScriptPubKeyの32バイトのハッシュと一致すると、スクリプトコマンドとして解釈される。
p2sh-p2wpkhと同様に後方互換性をもたせる。
ウォレット、階層的決定正ウォレット、ペイメントチャネルとLightning Networkなどについて学ぶと良い。テストネットのウォレットやブロックエクスプローラーなどを作ることもよいだろう。