RNGne Processor:

Random Number Generator from Natural Entropy

Encapsulates the logic for extracting random bits from an image and calculating Shannon Entropy & Rényi Min-Entropy , and uses a cryptographic extractor to ensure a highly strong and secure seed obtained from the entropy of natural phenomena
Author: Roberto Aleman
Documentation:
v1: https://ventics.com/rngneprocessor/
v2: https://ventics.com/rngne-processor-v2-0/

Introduction:True Randomness from Natural Entropy

The RNGneProcessor class embodies the core concept that physical, chaotic phenomena are the ideal source for generating True Random Numbers (TRNGs). While algorithmic generators (PRNGs) are fast, they are mathematically predictable. True security, especially in cryptography, requires unpredictability drawn from the physical world.

The RNGne project implements a robust two-phase approach to leverage this natural chaos for secure applications:

1. Extraction Phase (TRNG): Uses an image of a chaotic natural scene (like waves or lightning) to capture the random thermal noise of the camera sensor.
2. Amplification Phase (CSPRNG Seed): Converts the extracted raw entropy into a tiny, high-quality Cryptographic Master Seed via a cryptographic hash. This seed can then be mathematically amplified into a theoretically infinite stream of secure random numbers using a CSPRNG.

RNGne Processor PHP Class, Documentation

Core Operations and Methodology

The system operates by extracting the most volatile and noisy part of the image data: the Least Significant Bit (LSB).

1. Entropy Extraction (LSB Method)

The processImageForRandomBits() method performs the following low-level data extraction:

• Pixel Iteration: The function iterates through every pixel in the uploaded image.
• Grayscale Conversion: It averages the Red, Green, and Blue (RGB) components to find the single grayscale intensity value for that pixel.
• LSB Isolation: It isolates the Least Significant Bit (LSB) of the grayscale value using the modulo operator (% 2). This LSB is the part of the pixel data most likely to be affected by the unpredictable thermal and quantum noise of the camera sensor, making it the purest source of entropy.

2. Entropy Quality Test (Shannon's Formula)

The calculateShannonEntropy() method is the validation metric for the quality of the raw bits:

• Purpose: It measures the uncertainty or the average information content of the bit stream.
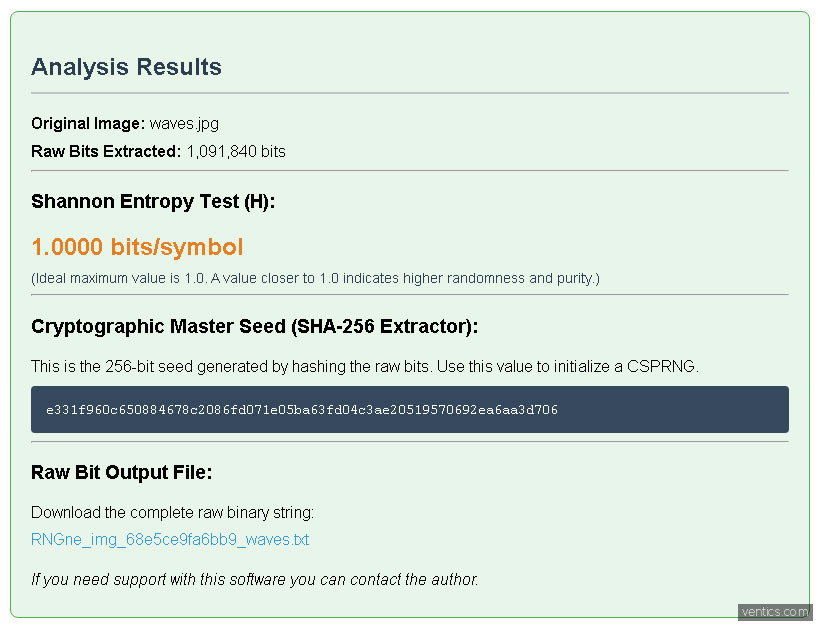
• Metric: The result is given in bits/symbol. A value of 1.0000 signifies a statistically perfect, uniform distribution of '0's and '1's (i.e., maximum randomness). Any deviation below 1.0000 indicates a measurable bias or pattern.

3. Cryptographic Extractor (SHA-256)

The extractMasterSeed() method performs the critical security transition:

• Input: The long string of raw, high-entropy bits.
• Process: It passes the entire bit string through the irreversible and collision-resistant SHA-256 hash function.
• Output: The result is a 256-bit Cryptographic Master Seed (a 64-character hexadecimal string). This process cleanses any remaining weak bias from the raw source and ensures the final seed is uniformly random and secure.

Validation Results: Proving Purity and Precision

To validate the RNGneProcessor, tests were conducted using sources ranging from zero entropy (control) to maximum entropy (ideal source).

Source Image	Description	Result (Shannon H)	Conclusion
Waves	High-complexity natural scene (Chaos, thermal noise).	1.0000 bits/pixel	Ideal Source Validation. Confirms the LSB of chaotic natural images yields maximum, unbiased entropy.
White square	Artificially uniform, pure white image (Control).	0.0000 bits/pixel	Zero Entropy Control. Confirms that predictable data (all LSBs are '1's) results in zero uncertainty.
Black Square	Artificially uniform, pure black image (Control).	0.0000 bits/pixel	Zero Entropy Control. Confirms that predictable data (all LSBs are '0's) results in zero uncertainty

The project's precision is demonstrated by its ability to accurately measure the entire range: from perfect predictability (0.0000) to the highest level of natural chaos (1.0000).

Requirements and Usage

RNGneProcessor is distributed for free under an open-source license.

Requirements:

• PHP 7.0+
• GD Extension (for image manipulation)

Best Practices for High Entropía Sources: To ensure the best possible Master Seed, users should prioritize images that maximize the sensor noise:

• Photos of chaotic elements: Lightning, ocean waves, dense foliage.
• Photos taken in low light conditions (which amplifies thermal noise).
• Use PNG or RAW image formats (lossless) to avoid compression artifacts that reduce real entropy.

Installation and Testing Guide for RNGne

This guide will walk you through setting up and validating the RNGne (Random Number Generator from Natural Entropy)

Step 1: File Setup

1. Create the Project Folder: Navigate to your web server's root directory and create a new folder named rngne.
2. Save the Code: Place the two PHP files inside this new rngne folder.
   • RNGneProcessor.php (The class containing the LSB extraction and SHA-256 logic).
   • upload_and_process.php (The web interface and controller).
3. Create the Upload Directory: Inside the rngne folder, create a new subdirectory named uploads.
4. Permissions: Ensure the uploads folder has write permissions (This is usually automatic on local Windows setups, but is essential for Linux/production servers).

Your Folder Structure Should Look Like This:

/rngne
|- RNGneProcessor.php
|- upload_and_process.php
|- /uploads (Empty folder, must be writable)

Step 2: Acquire a Test Image

To perform validation tests, you'll need two types of images:

1. High-Entropy Image (Ideal Source): An image of pure chaos, like ocean waves, static, deep-sky photography, or lightning. This should yield a Shannon Entropy of ?1.0000.
2. Zero-Entropy Image (Control Source): A solid black or solid white image. This should yield a Shannon Entropy of 0.0000.

Step 3: Execution and Validation

1. Start Your Server: Ensure your Apache web server is running.
2. Open the Tool: Open your web browser and navigate to your project URL (e.g., http://yourtestdomain/rngne/upload_and_process.php).
3. Perform Control Test (Zero Entropy):
   • Click "Select Image File" and upload your solid black or white control image.
   • Click "Extract & Generate Seed".
   • Validation Check: The Shannon Entropy Test (H) result should be near 0.0000 bits/symbol.
4. Perform Entropy Test (Ideal Source):
   • Click "Select Image File" and upload your high-entropy image (e.g., the image of the waves).
   • Click "Extract & Generate Seed".
   • Validation Check: The Shannon Entropy Test (H) result should be near 1.0000 bits/symbol.

If both tests pass, your RNGne system is correctly installed and functioning, and it is accurately converting the physical chaos of the image into a high-quality Cryptographic Master Seed.

---

RNGne Processor v2.0: From Nature to Solid Cryptographic Seed

Introduction: Raising the Quality of Natural Entropy The class RNGneProcessorhas evolved to version 2.0, consolidating its position as a robust tool for generating random seeds from natural phenomena (images). The core objective remains to extract the physical randomness inherent in image noise (vortices, waves, chaotic patterns) and purify it into a Cryptographic Master Seed using SHA-256.

The crucial improvement in this release is the integration of Rényi Entropies , enabling a security audit that goes beyond basic statistical analysis.

The Methodology: TRNG with Crypto Extractor The workflow RNGneProcessorcombines the physics of noise with the mathematics of safety:

Raw Entropy Harvesting ( Harvester ): The function processImageForRandomBits()extracts the Least Significant Bit (LSB) from each pixel, collecting the weakest and most chaotic noise source from the image. Quality Audit (Entropy): The quality of the extracted raw bits is measured using three different metrics, with emphasis on the “worst case.” Purity Extraction (Cryptographic Extraction): The function extractMasterSeed()uses SHA-256 to compress and remove any remaining bias in the raw entropy, ensuring a final 256-bit seed of complete purity.

The New Frontier: Rényi's Entropy for Security

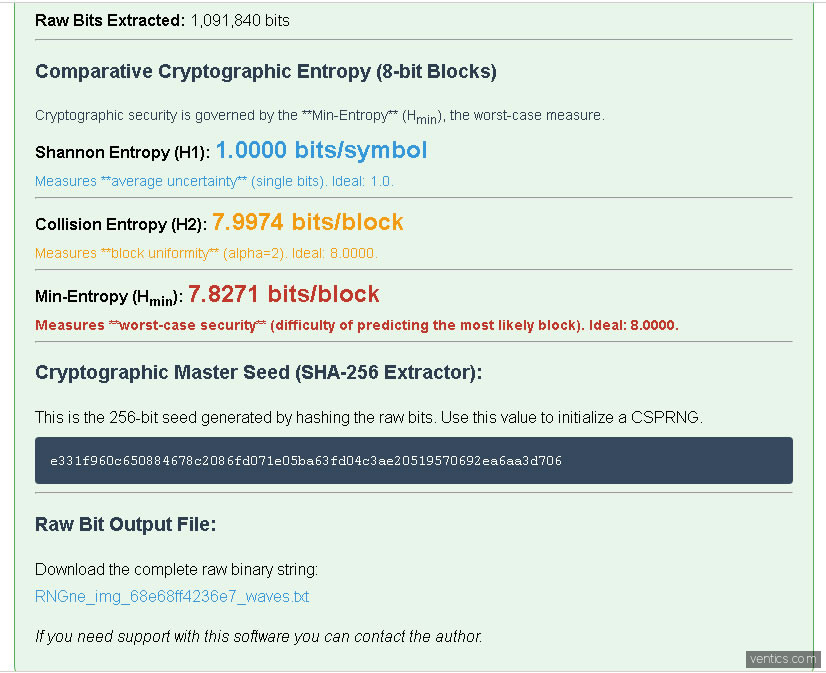
While Shannon entropy ( H1 ) is excellent for measuring overall imbalance (i.e., whether there are more zeros than ones), cryptography requires a more stringent measure. This is where Rényi entropies come in, measured in 8-bit (1-byte) blocks for standard security analysis:

Collision Entropy ( Hmin or α=2 )

What it measures: Block uniformity . It focuses on how far the distribution of the 256 possible bytes is from being perfectly flat. A value close to 8.0000 (for an 8-bit block) is ideal.

Significance: Helps confirm that the LSB extraction process is not favoring certain byte patterns beyond single-bit bias.

Minimum Entropy ( Hmin or H∞ )

What it measures: Worst-case security . This is the most important metric. It's calculated from the probability of the most frequent block in the entire bit sequence.

Hmin = −log2 ( Probability of the Most Frequent Block )

Importance: Hmin is the actual security value of the raw source. If the result is 7.8271 (as in real-life examples), it means the source is not perfectly random, fully justifying the use of the Crypto Extractor . Without this analysis, we would not know the risk level of the raw material.

Conclusion: The Necessary Cryptography

Comparing the results (ej., H1​ ≈1.0000 vs. Hmin ≈7.8271) is the acid test:

H1​ perfect(1.0) suggests a large statistical source. Hmin imperfect(e.g., 7.8271) reveals atiny deviationinherent in the physical process.

This small deviation is what the SHA-256 Extractor deterministically corrects . By hashing, the residual predictability (the missing 0.1729 bits) is removed and the final Master Seed is guaranteed to be a full 256 bits pure , ideal for initializing any Cryptographically Secure Pseudo-Random Number Generator (CSPRNG).

He RNGneProcessor v2.0 not only extracts randomness from nature, but uses the most rigorous tools of cryptography to certify and purify that randomness, making it suitable for the most demanding security environments.

What the Class Does (The Process)

 

The RNGneProcessor class executes a three-stage pipeline to generate a master cryptographic seed:

1. Entropy Harvester (Physical Input): The processImageForRandomBits() method extracts the Least Significant Bit (LSB) from the grayscale value of every pixel. This LSB acts as a collector of tiny, unpredictable physical noise (atmospheric disturbance, sensor noise) present in the image, yielding a long string of raw, physical random bits.
2. Comparative Cryptographic Audit (Rényi Analysis): The class calculates three critical entropy measures on the raw bit string (analyzed in 8-bit blocks):
   • Shannon Entropy (H1​): Measures the average uncertainty (basic 0 vs. 1 balance).
   • Collision Entropy (H2​): Measures the uniformity of the blocks (how flat the distribution of all 256 possible bytes is).
   • Min-Entropy (Hmin​ or H∞​): Measures the worst-case security. This identifies the probability of the single most likely block appearing, providing the true, minimum amount of randomness (in bits) available in the raw data.
3. Cryptographic Extractor: The extractMasterSeed() method uses the SHA-256 cryptographic hash function to process the raw bits. This step is essential because it eliminates any remaining statistical bias detected by the Hmin​ test.

 

What is Achieved with Version 2.0

 

The key achievement of V2.0 is the transition from a mere random bit generator to a certified cryptographic seed producer by explicitly addressing worst-case scenarios.

1. Quantified Security Level: The most important achievement is obtaining the Hmin​ value. This metric tells you exactly, in bits, how much true randomness is in your raw source (e.g., 7.8271 bits/block). This is the cryptographic standard for assessing the quality of a random source, which Shannon Entropy (H1​) cannot provide.
2. Justification of the Extractor: By showing that the raw entropy is typically high but slightly less than ideal (e.g., Hmin​<8.0000), the analysis cryptographically justifies the need for the SHA-256 extractor. The hash function acts as a high-quality "purifier" that guarantees the final 256-bit seed is free of all detectable bias, making it suitable for initializing a CSPRNG (Cryptographically Secure Pseudo-Random Number Generator).
3. Academic and Speculative Value: The comparative analysis facilitates deeper study (as we discussed), allowing users to quantify the "complexity" or "chaotic existence" of different natural phenomena. It provides a rigorous, universal metric to compare the randomness inherent in different physical sources.

---

Disclaimer. This software is provided as is. You are responsible for testing it at your own risk.