Data structures can be linear or non linear. In linear data structures, data elements are arranged sequentially, and each element is connected to its previous and next element. Examples include arrays, linked lists, stacks, and queues.
Non Linear data structures on the other hand, are those in which data elements are not arranged in a sequential manner. They are connected in such a way that each element is connected to two or more other elements. Examples include trees and graphs.
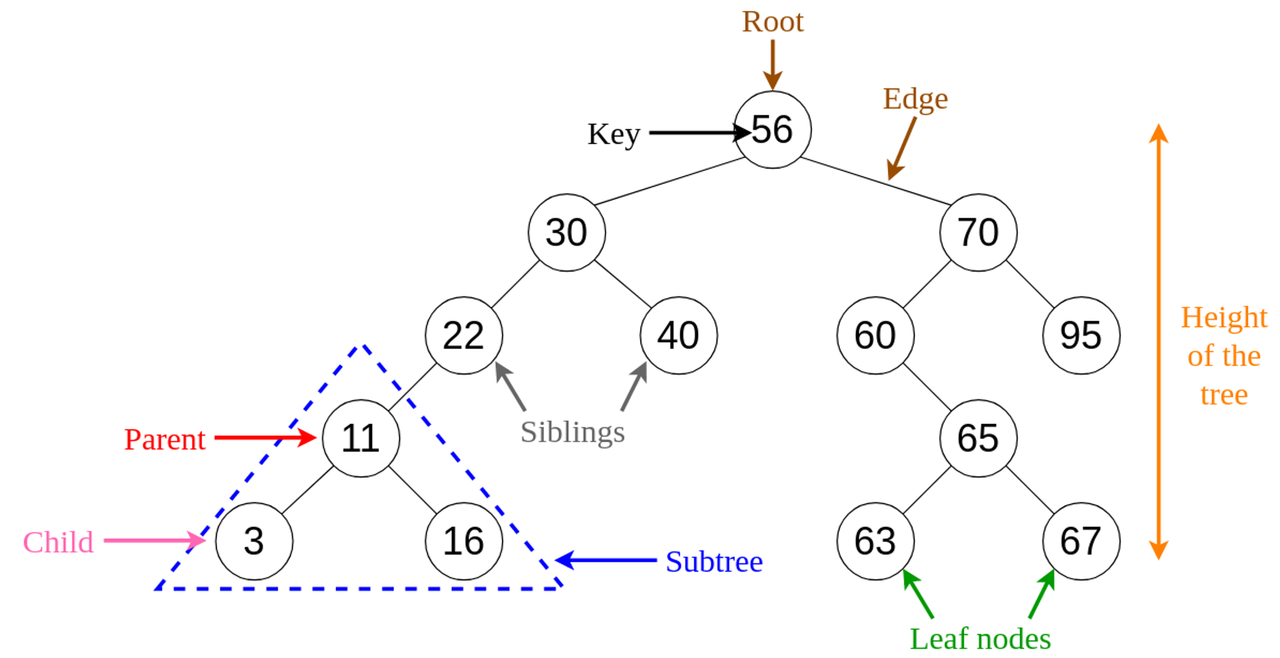
A binary tree is a type of tree data structure in which each node has at most two children, referred to as the left child and the right child. This makes binary trees especially useful for algorithms that search and sort data, as the structure allows for efficient operations.
A leaf node is considered a node which has no children.
Path: the path is the sequence of consecutive edges from source node to destination node.
Ancestor: is any predecessor node on the path from root to that node.
Descendent: any successor node on the path from that node to leaf node.
Sibling: children of the same parent.
Depth of node: the length of the path from root to that node.
Height of node: is the number of edges in the longest path from that node to a leaf.
Level of a node: is equal to the height of a tree, and level of a node is equal to the depth of a node.
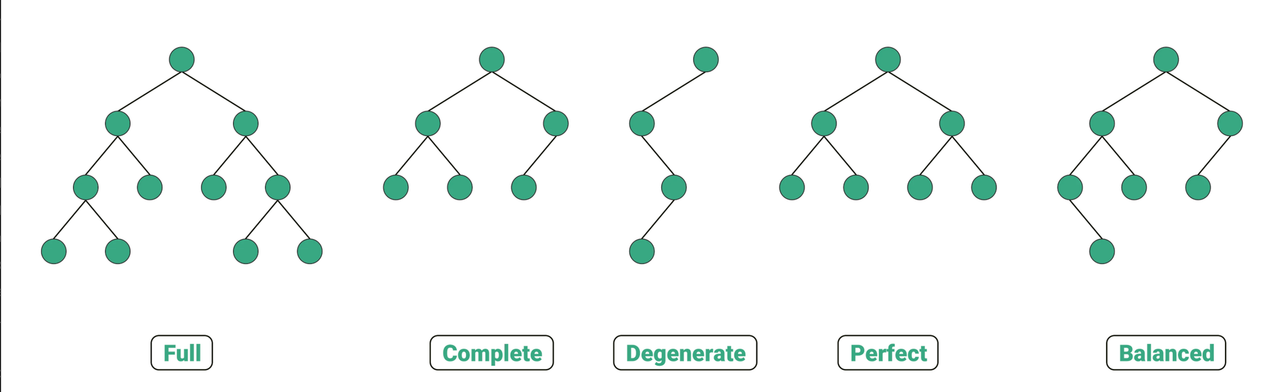
A full binary tree, also known as a proper or plane binary tree, is a type of binary tree where every node has either 0 or 2 children. That means, in a full binary tree, a node cannot have only one child. This property ensures that every level of the tree is fully filled.
A complete binary tree is a special type of binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. This means that you fill the nodes from left to right at each level before moving on to the next level. This property makes complete binary trees ideal for implementation as arrays. The parent-child relationship can be defined in terms of indices, which can make certain operations more efficient.
A perfect binary tree is a type of binary tree where all interior nodes have two children and all leaves have the same depth or same level. In other words, all levels of the tree are fully filled. This makes it 'perfect'. It's important to note that all perfect binary trees are also complete and full binary trees, but the reverse is not necessarily true.
A degenerate (or pathological) binary tree is a type of binary tree where every parent node has only one child. This means it's more like a linked list rather than a tree. In this case, the tree doesn't provide the benefits of a binary tree structure, such as efficient search, because each node only points to one other node.
There are several ways to traverse a binary tree:
-
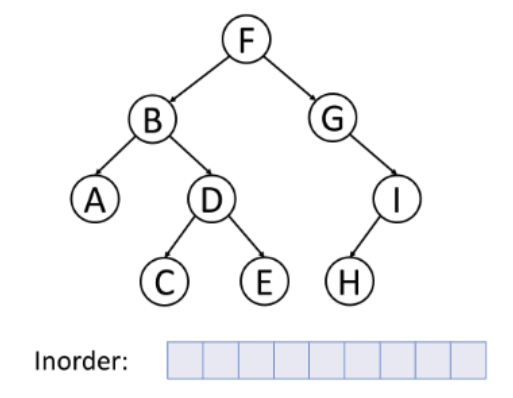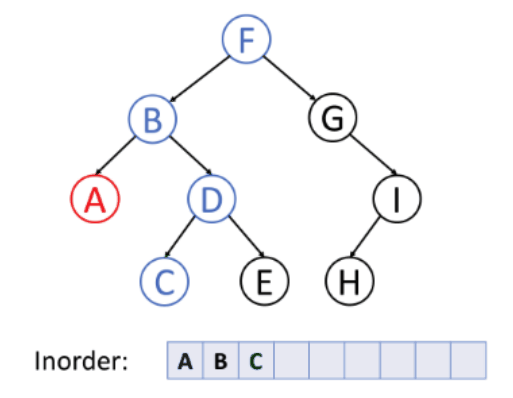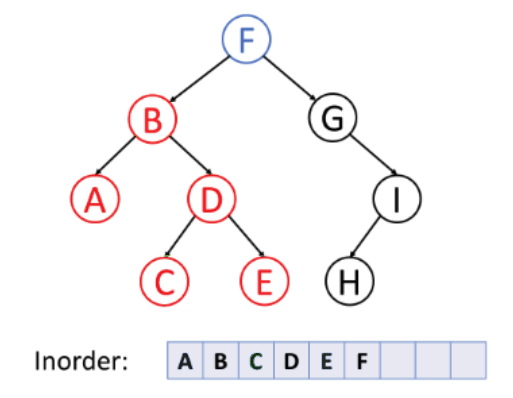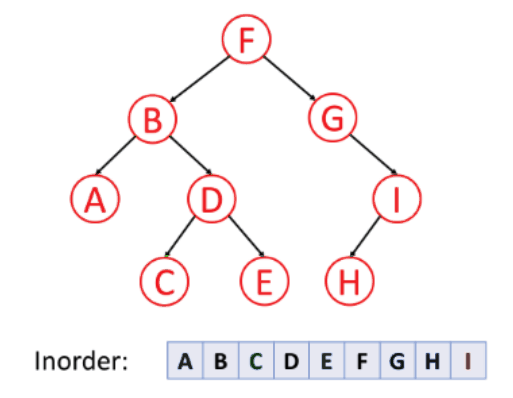
In-order Traversal: In this method, you first traverse the left subtree, then visit the root node, and finally traverse the right subtree. This is often used for binary search trees as it visits nodes in ascending order.
-
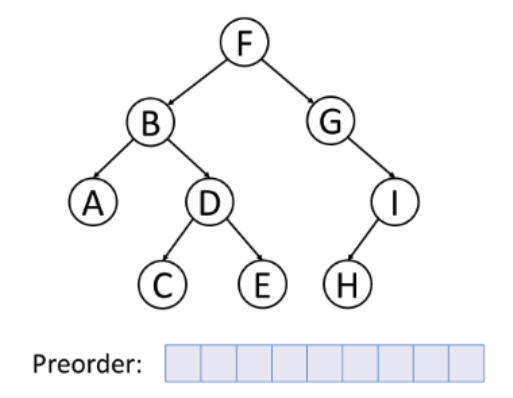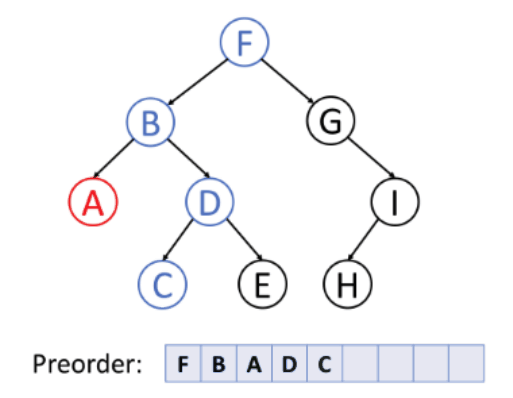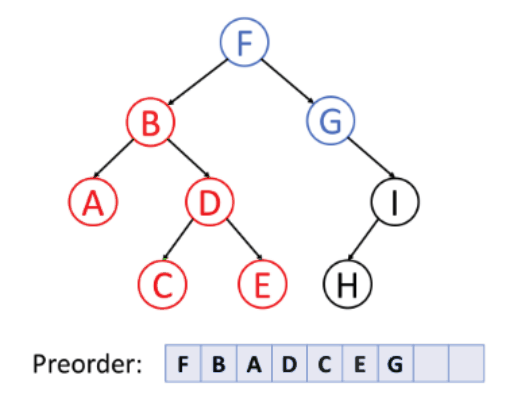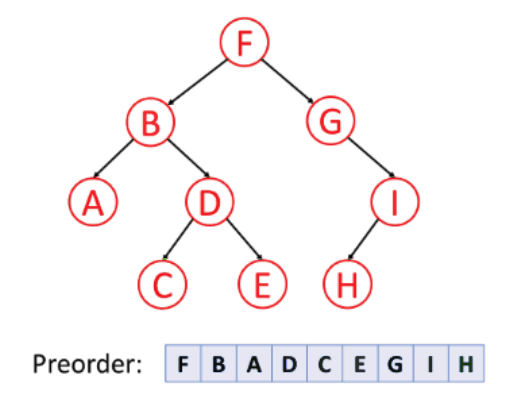
Pre-order Traversal: Here, you visit the root node first, then traverse the left subtree, and finally the right subtree. This is often used for copying or cloning a tree.
-
Post-order Traversal:In this method, you traverse the left subtree first, then the right subtree, and finally visit the root node. This is often used for deleting a tree. -
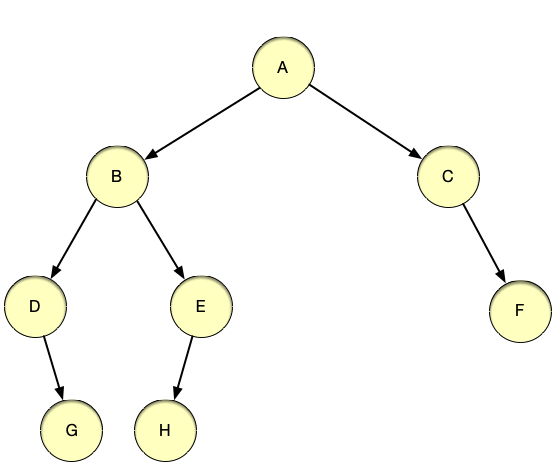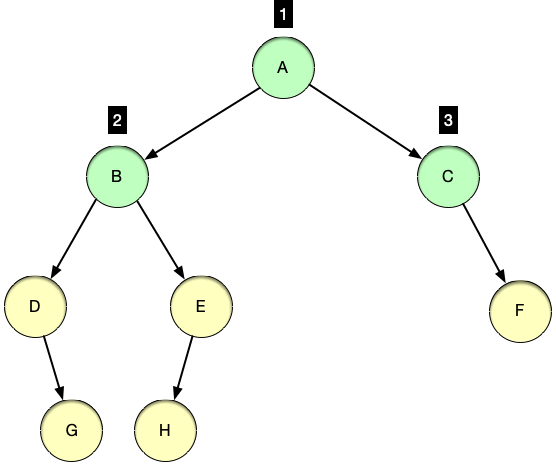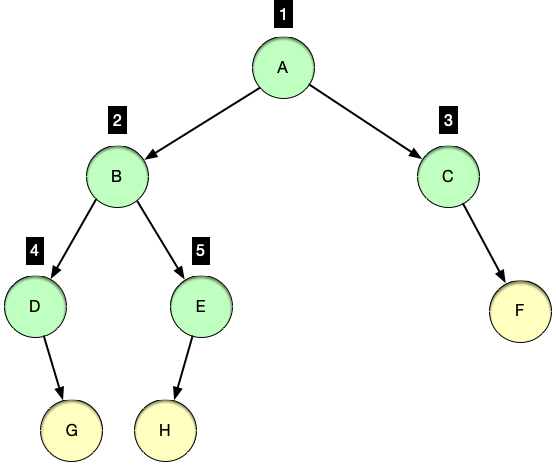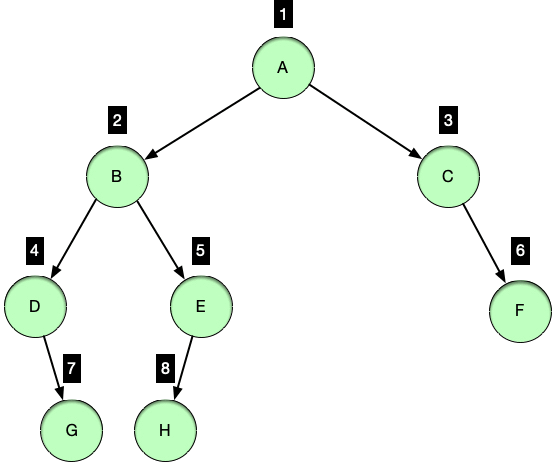
Level-order Traversal:Also known as Breadth-First Search (BFS), this method visits all the nodes of a level before going to the next level. This is often used for searching a tree.
A Binary Search Tree (BST) is a type of binary tree with a special property: for each node, all elements in its left subtree are less than the node, and all elements in its right subtree are greater than the node. This property makes BSTs useful for efficiently performing operations like search, insert, delete, etc. However, keep in mind that the efficiency of these operations in a BST depends on the height of the tree. In the best case, the tree is balanced and the height is log(n), where n is the number of nodes. In the worst case, the tree is skewed (all nodes are on one side of the root) and the height is n.
- In the best case, when the tree is balanced, the height is log(n), where n is the number of nodes. So, the time complexity for search, insertion, and deletion is O(log n).
- In the worst case, when the tree is skewed (all nodes are on one side of the root), the height is n. So, the time complexity for search, insertion, and deletion is O(n).
An AVL tree, named after its inventors Adelson-Velsky and Landis, is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one. If at any time they differ by more than one, rebalancing is done to restore this property. Rebalancing involves performing certain types of rotations on the tree. These are known as left rotation, right rotation, left-right rotation, and right-left rotation. The AVL tree maintains an O(log n) height, ensuring that operations like insertion, deletion, and search can be done in logarithmic time.
| Mode of Rotation | |
|---|---|
| Left-Left case | If the balance factor of the unbalanced node is positive and the balance factor of its left child is also positive (or zero), a right rotation on the unbalanced node is needed. |
| Right-Right case | If the balance factor of the unbalanced node is negative and the balance factor of its right child is also negative (or zero), a left rotation on the unbalanced node is needed. |
| Left-Right case | If the balance factor of the unbalanced node is positive and the balance factor of its left child is negative, a left rotation on the left child followed by a right rotation on the unbalanced node is needed. |
| Right-Left case | If the balance factor of the unbalanced node is negative and the balance factor of its right child is positive, a right rotation on the right child followed by a left rotation on the unbalanced node is needed. |
A Max Heap is a specialized tree-based data structure that satisfies the heap property. In a Max Heap, for any given node I, the value of I is greater than or equal to the values of its children. This property must be true across the entire tree. In other words, the parent node has a value greater than or equal to its children nodes, and the key of the root node is the largest among all other nodes. This property makes Max Heap useful for algorithms like Heap Sort, or for creating a priority queue.
The time complexity for operations like insertion and deletion in a Max Heap is O(log n), where n is the number of nodes. This is because these operations involve 'heapifying' the tree to maintain the heap property, which takes logarithmic time.
This project provides a comprehensive set of C functions for binary trees, covering basic operations, traversal methods, and specialized functionalities for binary search trees (BSTs), AVL trees, and max binary heaps.
- New Node, Insertion, Deletion: Create new nodes, insert them as children, and delete specified nodes.
- Leaf and Root Check: Determine if a node is a leaf or the root of the tree.
- Traversal: Perform pre-order, in-order, post-order, and level-order traversals.
- Tree Properties: Calculate height, depth, size, number of leaves and nodes, balance factor, and check for fullness and perfection.
- Is BST Check: Verify if the tree is a binary search tree.
- BST Operations: Insertion, search, and removal of nodes.
- Array to BST Conversion: Construct a BST from an array.
- Big O Analysis: Analyze time complexity for BST operations.
- Is AVL Check: Determine if the tree is an AVL tree.
- AVL Operations: Insertion, removal, and array to AVL tree conversion.
- Big O Analysis: Analyze time complexity for AVL tree operations.
- Is Binary Heap Check: Verify if the tree is a max binary heap.
- Heap Operations: Insertion, extraction of maximum element, and sorting.
- Array to Binary Heap Conversion: Construct a max binary heap from an array.
- Big O Analysis: Analyze time complexity for max binary heap operations.
These functions provide developers with efficient tools to manipulate and analyze binary trees, catering to a wide range of tree types and use cases.
To use the functions provided by this project, follow these steps:
- Clone the Repository:
$ git clone https://github.com/reunicorn1/binary_trees.git- Navigate to the Project Directory:
$ cd binary_trees- Compile the Source Code:
$ gcc -Wall -Wextra -Werror -pedantic binary_tree_print.c 0-main.c 0-binary_tree_node.c -o 0-nodeThis command compiles the source code into an executable named 0-node.
- Run the Executable:
$ ./0-nodeWe welcome contributions from the community to enhance this project. Here's how you can contribute:
- Fork the Repository: Fork the repository, clone it to your local machine, and make your changes.
- Open a Pull Request: Once your changes are ready, open a pull request from your fork to the original repository.
- Review and Approval: Your pull request will be reviewed, and upon approval, your changes will be merged into the main project.
Thank you for your contributions! We appreciate your efforts in making this project better for everyone.
The Binary_trees project is open-source and released under the MIT License. This license grants permission to anyone to use, modify, and distribute the software, subject to the conditions outlined in the license agreement.