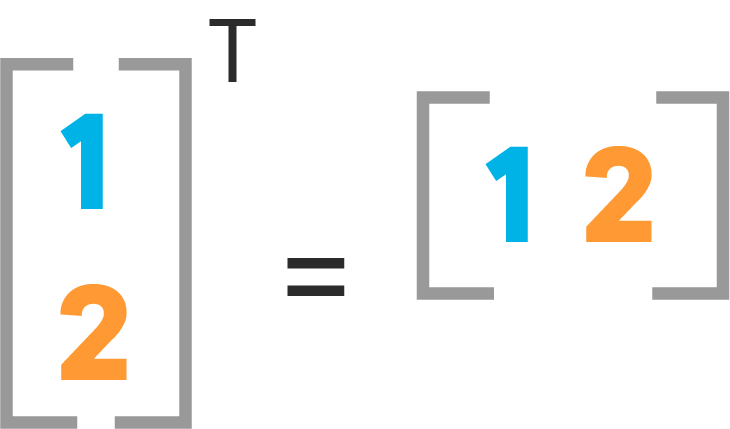In this lesson, you'll be introduced to the basic mathematical entities used in linear algebra. We'll also look at how these entities are created (and later manipulated) in Python using NumPy.
You will be able to:
- Compare scalars, vectors, matrices, and tensors
- Create vectors and matrices using Numpy and Python
- Use the transpose method to transpose Numpy matrices
Let's start by defining some mathematical entities that data scientists routinely come across while dealing with machine learning and deep learning algorithms. These entities are used to store, process and represent our data and analytical activities are mainly focused on manipulating these algebraic entities to provide solutions to unknown data entities.
A scalar is a single number
A scalar is the simplest entity in linear algebra compared to other objects, which are usually arrays of multiple numbers. In literature, you'll find scalars represented as lower case italics characters. Scalars need to be defined in terms of the type of number they carry. For example:
- Real valued scalars: Let $S \in \mathbb{R} $ be the salary of an individual
-
Natural number scalars: Let
$n \in \mathbb{N}$ be the number of floors in a building
A vector is an array of numbers arranged in some order, as opposed to the single numbered scalar.
The numbers contained within a vector are known as scalar components of the vector. Vectors are built from individual components, which are numerical in nature. We can think of a vector as a list of numbers, and vector algebra as operations performed on the numbers in the list.
\begin{equation} x = \begin{bmatrix} x_{1} \ x_{2} \ \vdots \ x_{n-1} \ x_{n} \ \end{bmatrix} \end{equation}
Where
In machine learning systems like regression you saw earlier, the output variable is known as a target vector with the lowercase
We can set index values to elements of a vector by defining a set containing the indices and write the set as a subscript. For example, to access
A vector can be thought of as an entity that represents spatial coordinates in an n-dimensional space, where n is the number of dimensions. A vector can also represent a line from the origin of the vector space with a direction and a magnitude, based on scalar components. Below is an example of a vector in 3D vector space:
Let’s look at how to define a vector in Python.
In Python, one of the easiest ways to represent a vector is by using Numpy arrays. The list scalar values can be used to create a vector in Python as shown below:
# create a vector from list [2,4,6]
import numpy as np
v = np.array([2, 4, 6])
print(v)# Code here There will be times when you have a lot of data in a vector (or array as we now know it) and you want to extract a portion of the data for some analysis. For example, maybe you want to know the first few values of a long array, or you want the integral of data between
x = np.linspace(-np.pi, np.pi, 10)
print(x)# Code here You can use the index values to address individual scalar values within this vector, similar to Python list indexing as shown below:
print (x[0]) # first element
print (x[2]) # third element
print (x[-1]) # last element
print (x[-2]) # second to last element# Code here You can select a range of elements too. The syntax a:b extracts the a-th to (b-1)-th elements. The syntax a:b:n starts at a, skips n elements up to the index b.
print (x[1:4]) # second to fourth element. Element 5 is not included
print (x[0:-1:2]) # every other element
print (x[:]) # print the whole vector
print (x[::-1]) # reverse the vector!# Code here A matrix is a 2-dimensional array of numbers written between square brackets.
As compared to vectors, a matrix is a multi-dimensional array of scalars that can possibly have multiple rows as well as columns. It is often denoted by an
We usually give matrices uppercase variable names with bold typeface, such as
A vector is a matrix that has only 1 column, so you have an
$(m \times 1)$ -matrix.$m$ is the number of rows, and 1 here is the number of columns, so a matrix with just one column is a vector.
As opposed to one-dimensional arrays used by vectors, we can represent a matrix in Python using a multi-dimensional NumPy array. A NumPy array can be constructed given a list of lists. For example, below is a 3 row, 3 column matrix created from a list of three lists.
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(X)# Code here - Note: Take special care with brackets during definition as opening and closing of the square brackets signifies a new row.
We can also define matlab styles matrices (for those used to matlab definitions) in the following way:
Y = np.mat([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(Y)# Code here Numpy matrices are always 2-dimensional, while numpy arrays (also referred to as ndarrays) are N-dimensional. Matrix objects are a subclass of ndarray, so they inherit all the attributes and methods of ndarrays. For multidimensional arrays/matrices with more than 2 dimensions, it is always best to use arrays. Arrays are the standard vector/matrix/tensor type of NumPy, and most NumPy functions return arrays and not matrices.
Arrays also offer a clear distinction between element-wise operations and linear algebra operations as you'll see later.
In 2D-arrays like the one we created above you can use a (row, column) notation. Use a : to indicate all rows or all columns. Remember that the indexing for both vectors and matrices start with 0 and ends at (m-1) and (n-1).
print (X[0, 0]) # element at first row and first column
print (X[-1, -1]) # element from the last row and last column
print (X[0, :]) # first row and all columns
print (X[:, 0]) # all rows and first column
print (X[:]) # all rows and all columns# Code here You can also use indexing to address and assign new values to elements of a matrix:
X[:, 0] = [11, 12, 13] # set the values in first column to this sequence
X[2, 2] = 15 # set a single element in third row and third column
print (X)
X[2] = 16 # sets everything in the third row to 16!
print (X)
X[:,2] = 17 # sets everything in the third column to 17!
print (X)# Code here The shape (or "dimensions") of a vector/matrix array tells us the number of values for each dimension. For a 2-dimensional array it gives you the number of rows and the number of columns. Let’s find the shape of our preceding 2-D and 3-D arrays created above. For a NumPy object, you can access its shape as shown below:
print(x.shape) # the vector with 10 scalars
print (X.shape) # the 2-D Matrix with 3X3 scalar components# Code here The vector has only one dimension as shown by the shape parameter whereas the 2D-matrix has 3 rows and 3 columns
Using transposition, you can convert a row vector to a column vector and vice versa. Let's see how its done in vectors and matrices.
Neural networks frequently process weights and inputs of different sizes where the dimensions do not meet the requirements of matrix multiplication. Matrix transpose provides a way to "rotate" one of the matrices so that the operation complies with multiplication requirements and can continue. There are two steps to transpose a matrix:
- Rotate the matrix right 90° clockwise.
- Reverse the order of elements in each row (e.g. [a b c] becomes [c b a]). This can be better understood looking at this image :
Numpy provides the transpose operation by using the .T attribute or the np.transpose() function with the array that needs to be transposed as shown below:
# create a transpose of a matrix
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
A_transposed = A.T
A_transposed_2 = np.transpose(A)
print(A,'\n\n', A_transposed, '\n\n', A_transposed_2)# Code here In some cases, you'll need an array with more than two axes. In the general case:
An array of numbers arranged on a regular grid with a variable number of axes is known as a tensor.
A vector is a one-dimensional or "first order tensor" and a matrix is a two-dimensional or "second order tensor". Tensor notation is just like matrix notation, with a capital letter that represents a tensor, and lowercase letters with a subscript representing scalar values within the tensor. Many operations that can be performed with scalars, vectors, and matrices can be reformulated to be performed with tensors as well. The image below shows some of these operations for a 3D tensor.
As a tool, tensors and tensor algebra are widely used in the fields of physics and engineering, and in data science it is particularly useful when you'll learn about deep learning models. We'll revisit tensors and relevant operations in the deep learning sections and explain how tensors are created, manipulated, and saved using more advanced analytical tools like Keras.
In this lesson, you learned about basic mathematical entities including scalars, vectors, matrices, and tensors to solve linear algebraic problems. You focused on creating vectors and matrices in Python and Numpy. You also saw how to index and slice these entities and check for the shape of underlying data elements. Next, you'll look at some of the key operations with matrices and vectors.