-
Notifications
You must be signed in to change notification settings - Fork 132
WIP augmented Lagrangian solver for adding equality constraints #457
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
base: main
Are you sure you want to change the base?
Conversation
|
@mhmukadam @luisenp - do you think it makes sense to continue and try to move this prototype into an |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Thanks for working on this @bamos and @dishank-b, this is great!
I left some comments for discussion on the overall design. I think it's also OK if for a first draft we manually set up all the different terms in the augmented lagrangian to test things out (e.g., just add any extra terms necessary when creating the objective). Once we settle on a good representation for the equality constraints and multipliers, we can figure out how to automate this with an AugmentedLagrangian class, which is a suggestion that I like.
| num_augmented_lagrangian_iterations=10, | ||
| callback=None, | ||
| ): | ||
| def err_fn_augmented(optim_vars, aux_vars): |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
I'm thinking it might be better (cleaner and more efficient) to introduce extra cost function terms for the constraints terms in the augmented Lagrangian, rather than extend to a new function with a larger error dimension. That is, the second row here would have its own cost function terms:
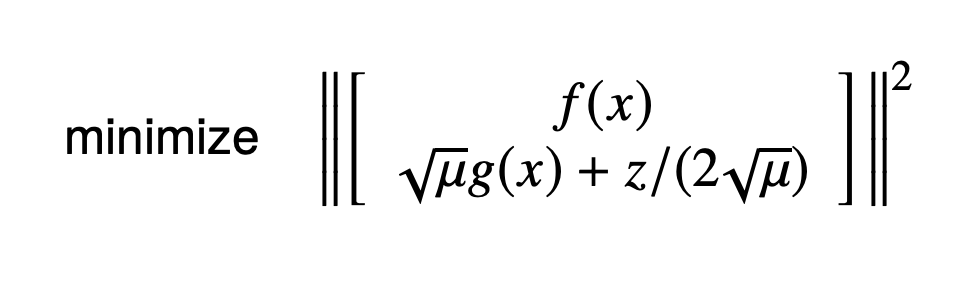
and Theseus already minimizes for the sum of squares internally. In terms of code, I think this should just involve moving the err_augmented term to its own CostFunction object. I see the following advantages:
- If the original error provides jacobian implementation, we can still use them rather than deferring to torch autograd once we put the original error in the augmented error function.
- More computationally efficient for sparse solvers, because the block jacobians should be of smaller size.
- If the user provides jacobians
dg(x)/dx, it should be easier to manually compute the jacobians of the augmented Lagrangian terms compared to the current approach. - The resulting code will be cleaner, but this is maybe a more subjective point.
One disadvantage of this approach is that we don't allow objectives from being modified (costs added/deleted) after the optimizer is created, but we should be able to get around this with an AugmentedLagrangianclass in a number of ways. I think for now, we can proof of concept things by manually adding the extra costs at the beginning of the example, just to get a feel for how things would look like. We can then figure out how to automate this process later.
| combined_err = torch.cat([original_err, err_augmented], axis=-1) | ||
| return combined_err | ||
|
|
||
| g = equality_constraint_fn(optim_vars, aux_vars) |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
For this, I like the RobustCost-style wrapper, as you mentioned in the TODOs. Something like
equality_constraint = th.EqualityConstraint(th.AutoDiffCostFunction(...))Following on the other comment above, a class like AugmentedLagrangian could then iterate over all cost functions in the objective, and add extra cost terms for any costs of type EqualityConstraint that computes the err_augmented term corresponding to each equality constraint.
This has some examples and a prototype @dishank-b and I created to help us get in equality constraints with an augmented Lagrangian method as described in this slide deck. It's appealing to have this method in Theseus because it relies mostly on the unconstrained GN/LM NLLS solvers we already have to solve for the update with the constraints moved into the objective as a penalty (via augmenting the Lagnangian). I created a
scratchdirectory (that we can delete before squashing and merging this PR) with fileaugmented_lagrangian.pythat implements an initial prototype of the method along with 2 examples inquadratic.pyandcar.pythat call into it.The quadratic example (
quadratic.py)This just makes sure we can solve
min_x ||x||^2 s.t. x_0 = 1, which has an analytic solution ofx^\star = [1., 0]and would make a good unit test once we've better-integrated this.Car example (
car.py)Solves this optimization problem:

We can reproduce this in a simple setting that goes from the origin to the upper right, but in general it doesn't seem as stable as what Vandenberghe has implemented:
Discussion on remaining design choices
I still don't see the best way of integrating the prototype in
augmented_lagrangian.pyinto Theseus. The rough changes are:equality_constraint_fn(gin the slides) that should equal zero.One option is to create a new
AugmentedLagrangianoptimizer class that adds the constraints, updates the cost, and then iteratively calls into an unconstrained solver. This seems appealing as the existing optimizer could be kept as a child and called into.Another design choice is how the user should specify the equality constraints. I've currently made the
equality_constraint_fnhave the same interface as a user-specifiederr_fnwhen usingAutoDiffCostFunction.TODOs once design choices are resolved
AutoDiffCostFunction. I think it could be done similar to https://github.com/facebookresearch/theseus/blob/main/theseus/core/robust_cost_function.pyscratchdirectoryEven more future directions