-
-
Notifications
You must be signed in to change notification settings - Fork 1.6k
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Arithmetic division for all types #8120
Arithmetic division for all types #8120
Conversation
I disagree here. We should use |
But |
Oops, my brain must have default it to Float32 like Int32.
I'm not sure. It is convenient to have a proper implementation of If we make Would that be comfortable enough? |
What's the difference between how
I think so. |
def //(other)
self.fdiv(other).floor
endAlso, in this pr |
|
Ooooh... sorry, I got confused. I meant to ask the difference between |
|
In any case having |
|
I second Asterite. I believe the cases where / should return a Float32 is when either lhs or rhs is a Float32 and the other isn't more significant (not Float64, BigX or Complex). |
|
I disabled some Big* specs in 32 bits. It seems that we stumble on that in the past already 7282cf3 . This should be ready for review. |
|
I still don't quite understand why |
|
Ah, yes, I think Int / Float32 should be Float32. Float64 should only be the default when two integers are. involved. And when doing Int / Float64 of course. |
|
@ysbaddaden, but [U]Int128 / Float32 => Float64, right? It’s good that I kept the colored table 😅 |
|
I don't think [U]Int128 / Float32 should be an exception. Any primitive integer divided by Float32 should be Float32. |
|
But then to keep the typing rule symmetrical there are some operations that will not fit: 1f32 / UInt128::MAX ≈ 2.938e-39 < 1.175e-38 ≈ Float32::MIN_POSITIVE It also bugs me a little that if Int / Float32 is Float32, then the typing rule formulation is a bit more complex, but is paperwork on the formality side. I will leave on the side. |
|
I think |
|
@bcardiff the same reasoning applies to all other binary operations with a Float32. Lower precision means that the value will be rounded, so I don't understand why There are use cases where we want lower precision. While documenting on alternative float sizes (16, 80 an 128-bit) I read that AI / ML algorithms sometimes cast to Float16 to specifically lose precision, which reduces memory usage, but also improves results: AI behaves better with blurry results, being too precise is counter productive. |
|
@ysbaddaden yes I recall the same use cases even losing some precision. For native types:
For extensions:
with that, the table will look like follows Separating native types and extensions seem needed because otherwise Float64 * BigInt would've been Float64 according to the rules for native types, instead of BigFloat which I think is preferred. 👍 ? |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
👍
ddbaf9d to
1cffcc5
Compare
|
Rebased on master and apply some suggested changes in the spec. I triggered a test build so I can check early how good we to ship this in 0.31.0 |
crystal-lang/crystal#8120 changed the behavior of `/` to always return floats.
|
Do other languages do this? I'm so used to 3/2==1 being true. |
|
@elorest Nim, Python, Elm, Haskell, Perl, to name a few. |
|
@asterite thanks. |
|
For the floor division of a Float, it will be logical to return an Integer instead of a Float.
For now we have What do you think? It will make sense on the mathematical level, but maybe not on the Crystal language one, where usually calling a method on a type returns the same type. |
|
For example, in Julia: x = floor(1 / 2)
print(typeof(x)) #=> Float64x = floor(Int, 1 / 2)
print(typeof(x)) #=> IntI guess the actual behavior in Crystal makes also sense, I'm just going to add |
|
The reason is that the range of a Float64 is bigger than that of an Int32 (or Int64). So if you do |
|
Another solution I came across for those wanting more mathematical "correctness" is to use Big. |

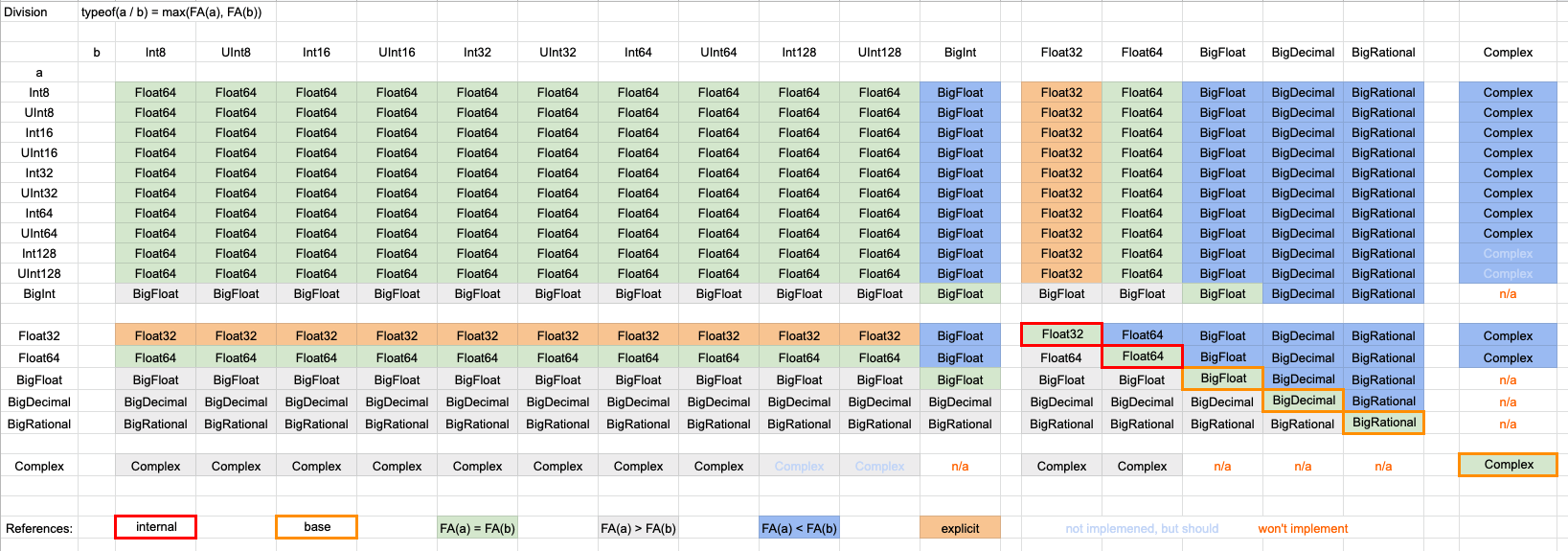
Note: Final behavior described at #8120 (comment)
This PR makes
/work as arithmetic division for all types.As a reminder, for integer or floor division
//should be used.Given a binary operator
⨁, the result type is usually the type of the left hand side:typeof(a ⨁ b) == typeof(a). This helps to reduce the unions in expressions likea ⨁= b.For
/this rule does not apply since the type might be a different to the operands. We wantanInt32 / anInt32to beFloat32.There are 17 "numeric" types in the stdlib:
[U]Int{8,16,32,64,128}, Float{32,64}, Big{Int,Float,Decimal,Rational}, Complex. (Actually,Complexdoes not inherit fromNumber.)I propose
typeof(a / b) == max(fa(typeof(a)), fa(typeof(b))), wherefa(t)defines a float affinity type.Float32ift = [U]Int{8,16,32,64}Float64ift = [U]Int128UInt128::MAX≈ 2.938e-39 < 1.175e-38 ≈Float32::MIN_POSITIVEBigFloatift = BigInttift = Float{32,64},Big{Float,Decimal,Rational},ComplexAnd
maxis computed under the partial order inferred by{Float32 < Float64, Float64 < BigFloat < BigDecimal < BigRational, Float64 < Complex}All the combinations can be viewed in the following table:
The
maxrelation is not defined forComplexandBig{Int,Float,Decimal,Rational}, they are extensions to the basic numbers but they do not interact well within each other. And I don't see us addingBigRationalComplexin the std-lib.Note: I checked if
typeof(a / b) == fa(typeof(a))would be a good rule, to be more similar to the other operators . But checking how things likeloop { a = a / 2 }andloop { a = 2 / a }would work under one or another make me decide in favor oftypeof(a / b) == max(fa(typeof(a)), fa(typeof(b))).I have a couple of leftovers or further thoughts after these changes:
to_Xmethods or ininitialize/self.new? Is there a generic implementation overridden or implementation should be only in the concrete classes?spec/support/number.crI tried to avoid changing as less as possible, but there is still some work to do in order to get some neat implementation. But for now is an improvement and I needed to fill some missing gaps in
Big*related to conversions.Fixes #2968