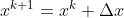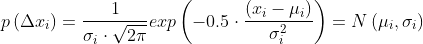Random search algorithm

A simple n-dimensional random search algorithm.

Introduction

The Random search algorithm was the first method that based its optimization strategy on a stochastic process. Only one solution 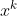is kept during the evolution process. In each iteration, the solution 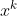is modified by adding a random vector 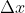. In this way the new solution is modeled under the following expression:

Considering that the solution 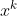has d dimensions 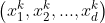, each coordinate is modified 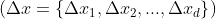by the random disturbance 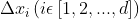modeled by a Gaussian probability distribution defined as:

where 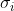and 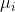, represent the standard deviation and the mean value, respectively for dimension i. Since the value of 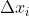adds a modification around 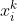, the mean value is considered zero .

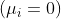Once 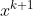has been calculated, it is tested whether the new position improves the quality of the previous solution 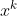. In this way, if the quality of 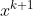is better than 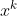, the value of 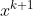is accepted as the new solution, otherwise 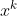remains unchanged.

Installation

GitHub

To install this library from GitHub run the following commands in the terminal:

$ git clone https://github.com/angelgaspar/randomsearch.git
$ cd randomsearch
$ python setup.py install

PyPi

If you have pip installed run the following commands in the terminal:

$ pip install randomsearch

Usage

This is an usage example:

import randomsearch as rs


def your_function(x):
    return -(x[0] ** 2 + x[1] ** 2) + 4


a, b = rs.optimize(function=your_function, dimensions=2, lower_boundary=[-14, -14], upper_boundary= [10, 10], max_iter=10000, maximize=True)
print(a, ",", b)

Note: The optimize function returns the best fitness and the best solution.
If you want to minimize a function maximize should be False.