MCHammer

Author:	Andrew Tarzia

A Monte Carlo-based molecular optimizer for optimizing the length of specified bonds in a molecule toward a target using cheap and unphysical potentials.

Please submit an issue with any questions or bugs!

Installation

Install using pip:

pip install mchammer

Algorithm

Subunits are the rigid bodies of a molecule. Substructures are the bonded interactions between them. There are nonbonded interactions between subunits too.

MCHammer implements a simple Metropolis Monte-Carlo algorithm to optimize the desired bonds toward a target bond length. We define a graph of the molecule at the atomic level, which is further coarse-grained into subunits that are separated by the bonds to be optimized. All atom positions/bond lengths within a subunit are kept rigid and do not contribute to the potential energy, other than through nonbonded interactions. The algorithm uses a simple Lennard-Jones nonbonded potential and parabolic bond potential to define the potential energy surface such that the target bond length is the energy mininum and steric clashes are avoided.

The MC algorithm is as follows:

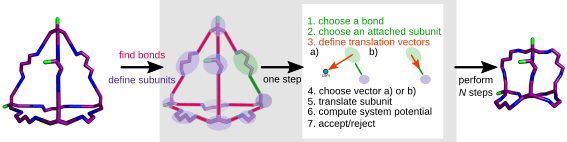
For step in N steps:

1. Choose a bond B at random.
2. Choose a subunit s on either side of B at random.

3. Define two possible translations of s, a and b and choose at random:

a is defined by a random number in [-1, 1) step along the s to molecule centre of mass (com). b is defined by a random number in [-1, 1) step along the vector B. Step size is defined by user input.

4. Compute system potential U = U_b + U_nb:

   U_b is the bonded potential, defined by the sum of all parabolic bond stretches about the target bond length for all B:

   U_b = sum_i (epsilon_b * (r_i - R_t)^2 ), where R_t is the target bond length, epsilon_b defines the strength of the potential and r_i is the ith bond length.

   U_nb is the nonbonded potential, defined by the repulsive part of the Lennard-Jones potential:

   U_nb = sum_i,j (epsilon_nb * (sigma / r_ij)^mu), where epsilon_nb defines the strength of the potential, sigma defines the position where the potential becomes repulsive, mu defines the steepness of the potential and r_ij is the pairwise distance between atoms i and j.

5. Accept or reject move:

   Accept if U_i < U_(i-1) or exp(-beta(U_i - U_(i-1)) > R , where R is a random number [0, 1) and beta is the inverse Boltzmann temperature. Reject otherwise.

The workflow for a porous organic cage built using stk (https://stk.readthedocs.io/) is shown schematically below (this example is shown in examples/stk_example.py):

Examples

This code was originally written for use with stk (https://stk.readthedocs.io/), which assembles structures with long bonds that we wanted to optimize quickly. Now it has been generalized to take any molecule (defined by atoms and bonds) and a set of bonds to optimize to some target bond length. The algorithm is unphysical in that the bonded and nonbonded potential we apply is meaningless, other than to give a reasonable structure for further optimisation or use in a workflow!

The Optimizer class provides two main method: get_result and get_trajectory , which provide the optimized structure and properties or the structure and properties of each MC step, respectively. The molecule at each step of the trajectory and its properties can be collected from the results of the get_trajectory method, but not the get_result method (the example file: examples/minimum_example.py shows how to plot the optimisation progress and output the trajectory).

In this example, we use stk for I/O only with the input file available in examples/minimum_example.py:

import stk
import mchammer as mch


benzene = stk.BuildingBlock.init_from_file('benzene.mol')
benzene_atoms = [
    (atom.get_id(), atom.__class__.__name__)
    for atom in benzene.get_atoms()
]
benzene_bonds = []
for i, bond in enumerate(benzene.get_bonds()):
    b_ids = (bond.get_atom1().get_id(), bond.get_atom2().get_id())
    benzene_bonds.append((i, b_ids))

mch_mol = mch.Molecule(
    atoms=(
        mch.Atom(id=i[0], element_string=i[1])
        for i in benzene_atoms
    ),
    bonds=(
        mch.Bond(id=i[0], atom_ids=i[1])
        for i in benzene_bonds
    ),
    position_matrix=benzene.get_position_matrix(),
)

target_bond_length = 1.2
optimizer = mch.Optimizer(
    step_size=0.25,
    target_bond_length=target_bond_length,
    num_steps=100,
)
subunits = mch_mol.get_subunits(
    bond_pair_ids=((2, 3), (1, 5)),
)
# Get all steps.
mch_mol, mch_result = optimizer.get_trajectory(
    mol=mch_mol,
    bond_pair_ids=((2, 3), (1, 5)),
    subunits=subunits,
)
# Update stk Molecule with new position matrix.
benzene = benzene.with_position_matrix(
    mch_mol.get_position_matrix()
)
benzene.write('benzene_opt.mol')

Finally, we mention that the Optimizer.get_subunits() is based on splitting the Molecule by the input bond_pair_ids. This method is now public, so that users can modify the defined subunits to enforce rigid non-covalent interactions. I.e. non-covalent complexes will be distinct subunits because there is no bond between them, and the user can merge them into one subunit by merging the iterable of atom ids in the subunits dictionary, to force the algorithm to treat them as one rigid body. An example of this is given in examples/stk_example.py using an arbitrary non-covalent complex BuildingBlock.

As part of this code, I also provide the Collapser class, which is a naive precursor to MCHammer that simply moves all subunits toward the molecule centroid until a distance threshold is met. This can sometimes be faster than MCHammer for some molecule types. An example of this is shown in examples/collapser_example.py.

Contributors and Acknowledgements

I developed this code as a post doc in the Jelfs research group at Imperial College London (<http://www.jelfs-group.org/>, <https://github.com/JelfsMaterialsGroup>).

This code was reviewed and edited by: Lukas Turcani (<https://github.com/lukasturcani>), Steven Bennett (<https://github.com/stevenbennett96>)

License

This project is licensed under the MIT license.