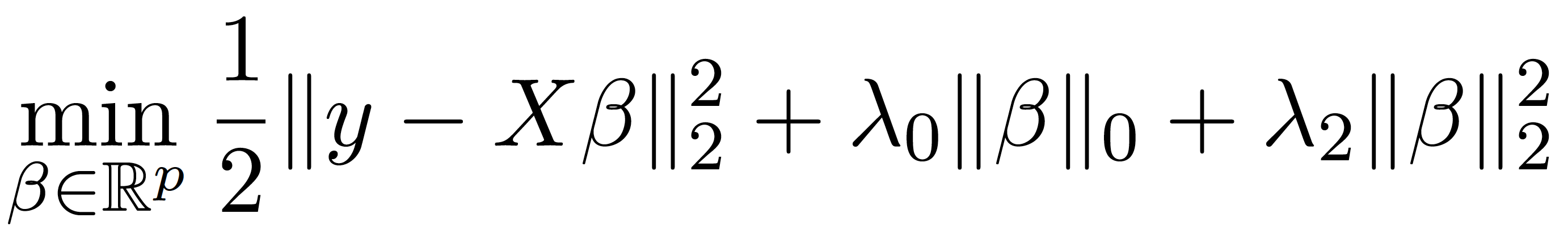L0BnB is a scalable global optimization framework for solving linear regression problems penalized with a combination of the L0 and L2 norms. More concretely, given a data matrix X (with n samples and p features) and a response vector y, L0BnB solves the following problem to optimality:
where the L0 (pseudo)-norm counts the number of nonzeros in the coefficients vector B. Here the L0 (pseudo)-norm performs variable selection, while the L2 norm adds shrinkage which can be particularly useful in low-signal settings. L0BnB implements a custom branch-and-bound (BnB) framework that leverages a highly specialized first-order method to solve the node subproblems. It achieves over 3600x speed-ups compared to the state-of-the-art mixed integer programming (MIP) solvers, and can scale to problems where the number of features p ~ 10^7. For more details, check out our paper Sparse Regression at Scale: Branch-and-Bound rooted in First Order Optimization (arXiv link).
The toolkit is implemented in Python 3. To install it, run the following command:
pip install l0bnbimport numpy as np
from l0bnb import fit_path
from l0bnb import gen_synthetic
"""
For demonstration, we first generate a synthetic regression dataset (X,y)
as follows: y = X*b + epsilon, where the true vector of coefficients b
is sparse and has only 10 nonzero entries.
We set the number of samples n=1000 and number of features p=10,000.
"""
X, y, b = gen_synthetic(n=1000, p=10000, supp_size=10)
print("Nonzero indices in b: ", np.nonzero(b)[0])
"""
Run L0BnB to solve the problem for a sequence of lambda_0's.
By default, the sequence of lambda_0's is automatically chosen by the toolkit.
Use max_nonzeros=10 to stop the regularization path when it exceeds 10 nonzeros.
Here we fix lambda_2 = 0.01 (generally, this is data-dependent).
"""
sols = fit_path(X, y, lambda_2 = 0.01, max_nonzeros = 10)
"""
sols is a list of solutions, each corresponding to a different lambda_0.
Below we inspect the solution with index 4.
The estimated coefficients vector "b_estimated" and the intercept term can be accessed as follows:
"""
b_estimated = sols[4]["B"] # a numpy array.
intercept = sols[4]["B0"]
# To check the nonzero indices in b_estimated:
print("Nonzero indices in b_estimated: ", np.nonzero(b_estimated)[0])
# The nonzero indices in b_estimated match that of b.
# Predictions on the training data can be made as follows:
y_estimated = np.dot(X, b_estimated) + intercept
# For more advanced usage, check the documentation of fit_path:
print(fit_path.__doc__)If you find L0BnB useful in your research, please consider citing the following paper:
@article{hazimeh2021sparse,
title={Sparse regression at scale: Branch-and-bound rooted in first-order optimization},
author={Hazimeh, Hussein and Mazumder, Rahul and Saab, Ali},
journal={Mathematical Programming},
pages={1--42},
year={2021},
publisher={Springer}
}