Plot complex-valued functions with style.

cplot helps plotting complex-valued functions in a visually appealing manner.

Install with

pip install cplot

and use as

import numpy as np

import cplot


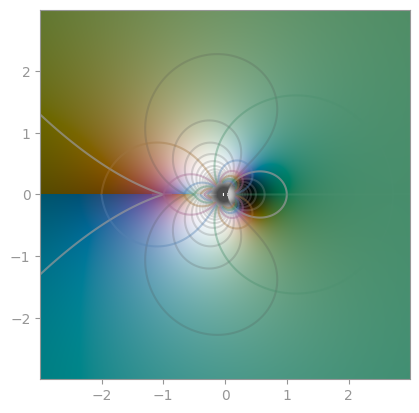
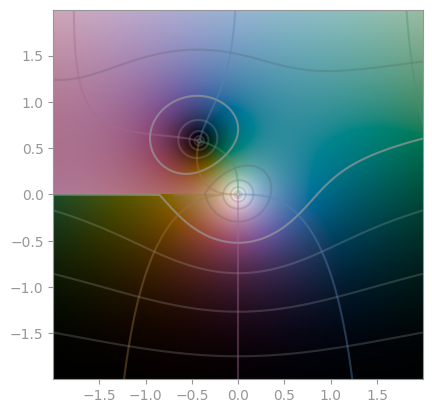
def f(z):
    return np.sin(z**3) / z


plt = cplot.plot(
    f,
    (-2.0, +2.0, 400),
    (-2.0, +2.0, 400),
    # abs_scaling=lambda x: x / (x + 1),  # how to scale the lightness in domain coloring
    # contours_abs=2.0,
    # contours_arg=(-np.pi / 2, 0, np.pi / 2, np.pi),
    # emphasize_abs_contour_1: bool = True,
    # add_colorbars: bool = True,
    # add_axes_labels: bool = True,
    # saturation_adjustment: float = 1.28,
    # min_contour_length = None,
    # linewidth = None,
)
plt.show()

Historically, plotting of complex functions was in one of three ways

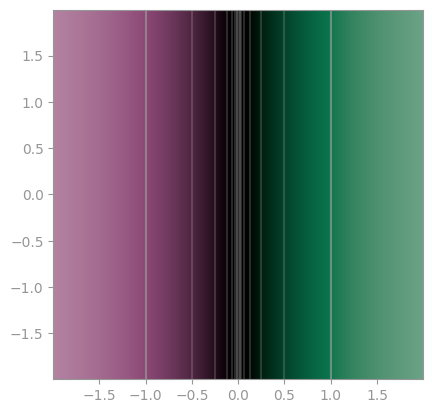
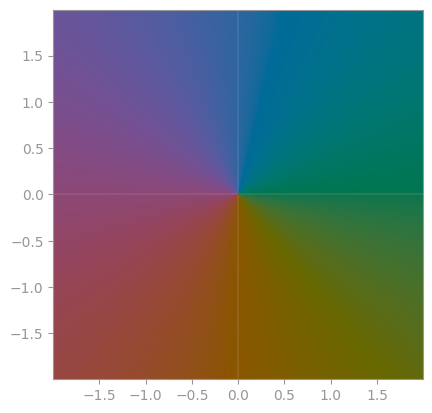
Only show the absolute value; sometimes as a 3D plot	Only show the phase/the argument in a color wheel (phase portrait)	Show contour lines for both arg and abs

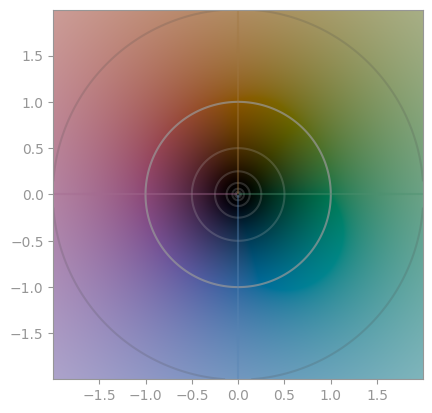
Combining all three of them gives you a cplot:

See also Wikipedia: Domain coloring.

Features of this software:

• cplot uses OKLAB, a perceptually uniform color space for the argument colors. This avoids streaks of colors occurring with other color spaces, e.g., HSL.
• The contour abs(z) == 1 is emphasized, other abs contours are at 2, 4, 8, etc. and 1/2, 1/4, 1/8, etc., respectively. This makes it easy to tell the absolte value precisely.
• For arg(z) == 0, the color is green, for arg(z) == pi/2 it's blue, for arg(z) = -pi / 2 it's orange, and for arg(z) = pi it's pink.

Other useful functions:

# There is a tripcolor function as well for triangulated 2D domains
cplot.tripcolor(triang, z)

# The function get_srgb1 returns the SRGB1 triple for every complex input value.
# (Accepts arrays, too.)
z = 2 + 5j
val = cplot.get_srgb1(z)

Riemann sphere

cplot can also plot functions on the Riemann sphere, a mapping of the complex plane to the unit ball.

import cplot
import numpy as np

cplot.riemann_sphere(np.log)

Gallery

All plots are created with default settings.

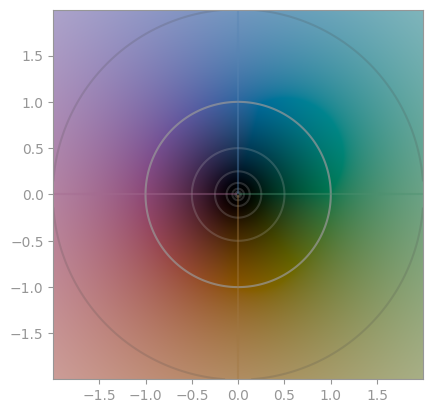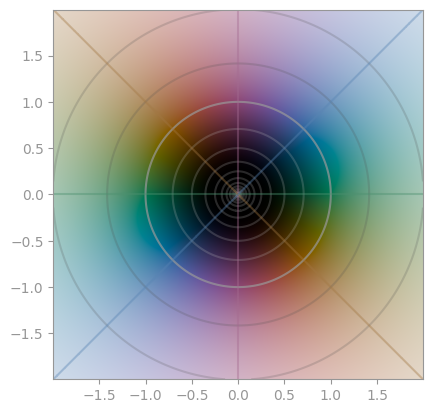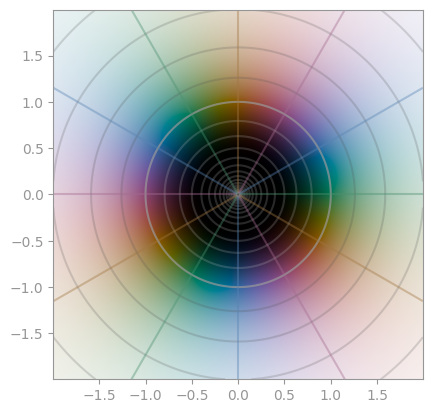z ** 1	z ** 2	z ** 3

Many more plots

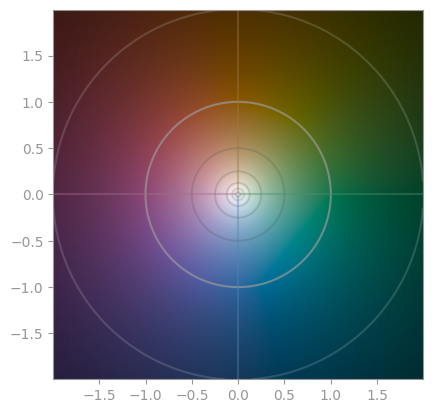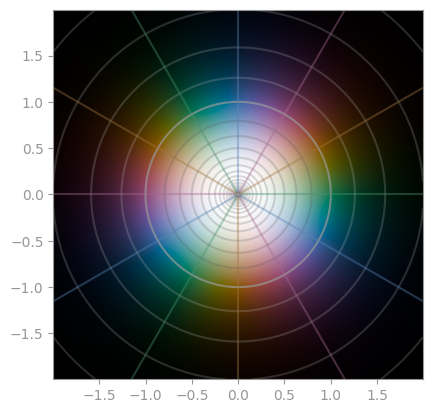1 / z	1 / z ** 2	1 / z ** 3

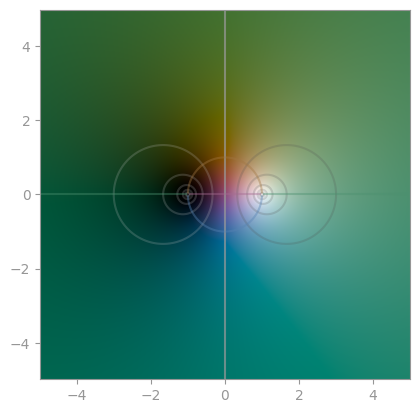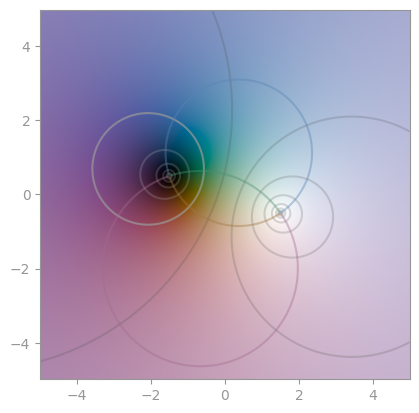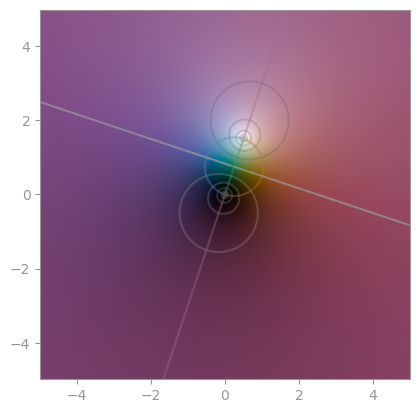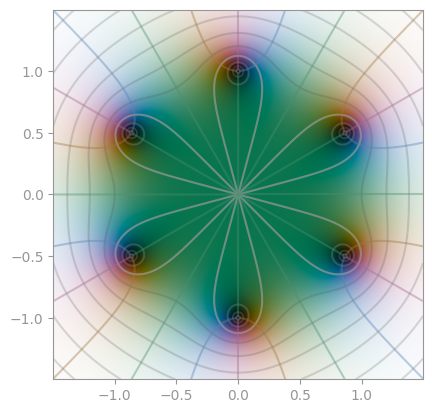
(z + 1) / (z - 1)	Another Möbius transformation	A third Möbius transformation

np.real	z / abs(z)	np.conj

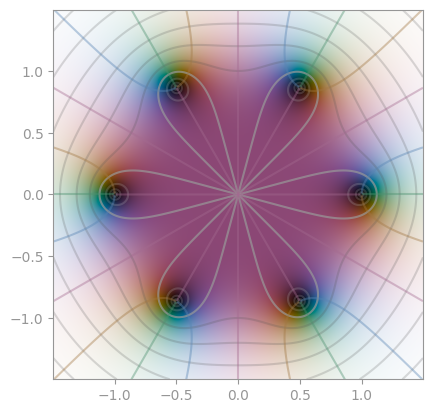
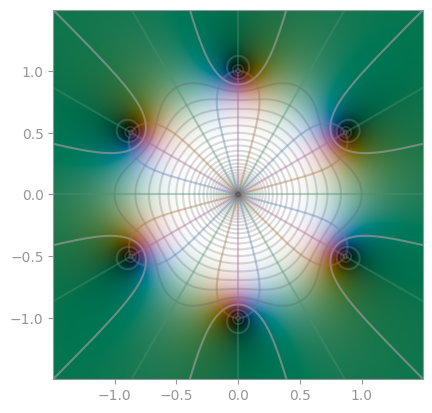
z ** 6 + 1	z ** 6 - 1	z ** (-6) + 1

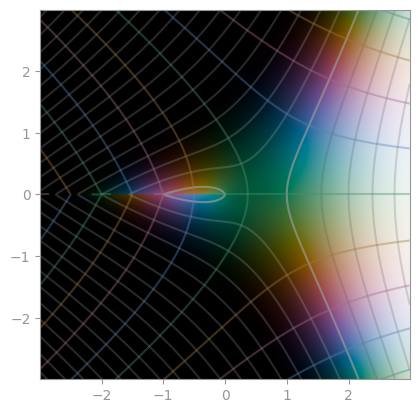
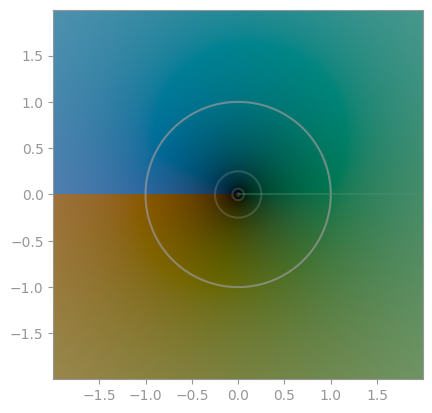
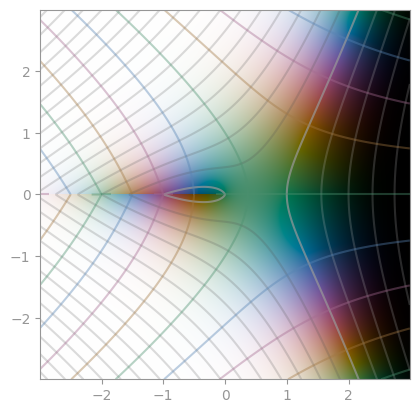
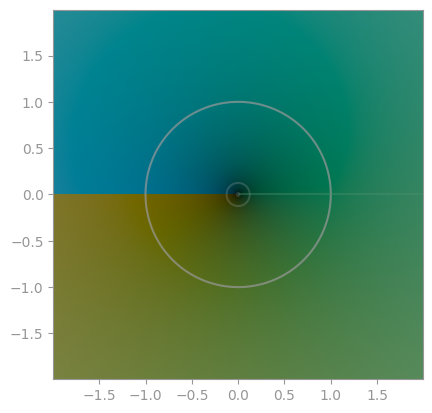
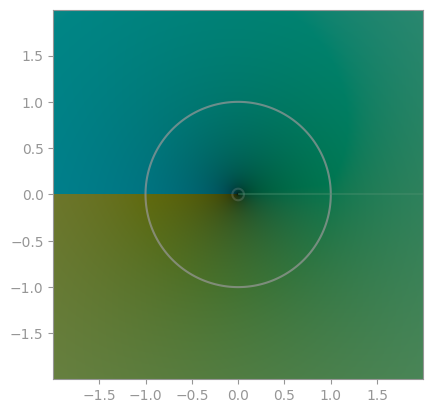
z ** z	(1/z) ** z	z ** (1/z)

np.sqrt	z**(1/3)	z**(1/4)

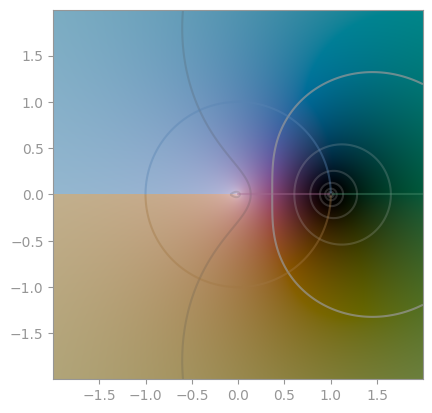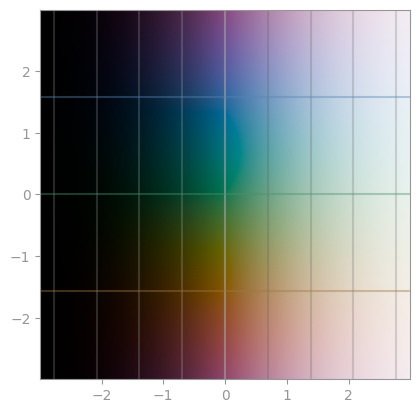
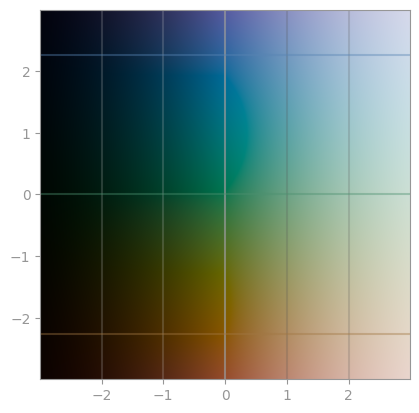
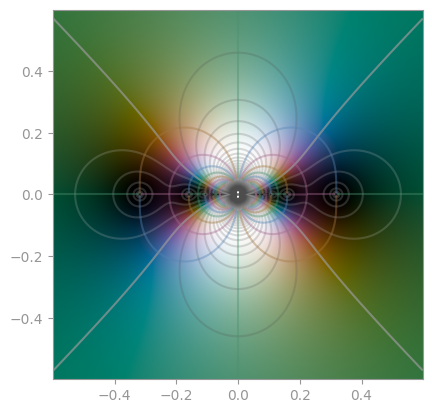
np.log	np.exp	np.exp2

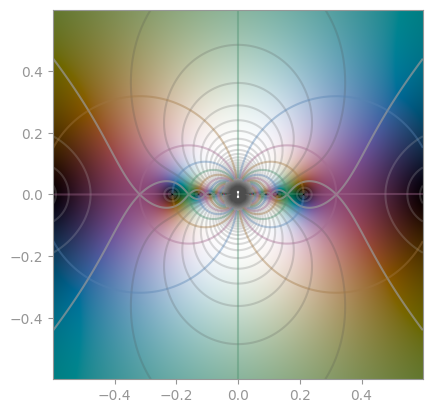
np.exp(1 / z)	z * np.sin(1 / z)	np.cos(1 / z)

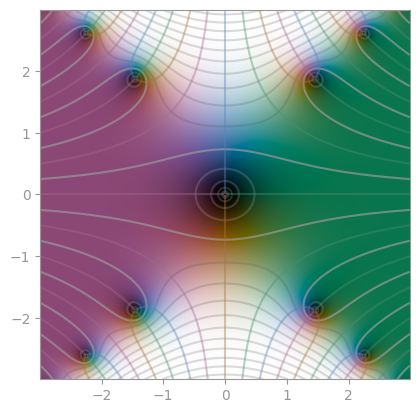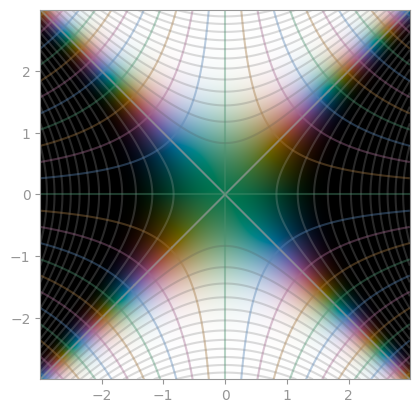
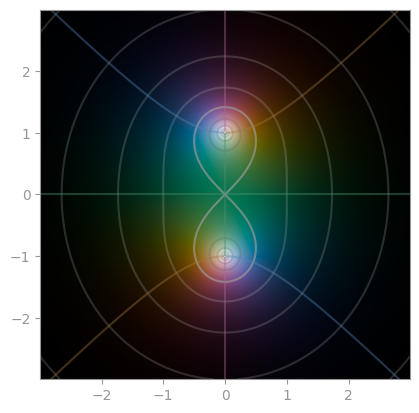
exp(- z ** 2)	1 / (1 + z ** 2)	Error function

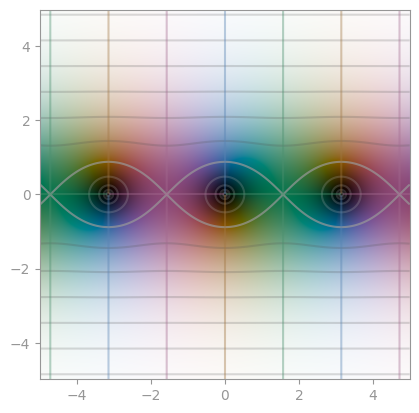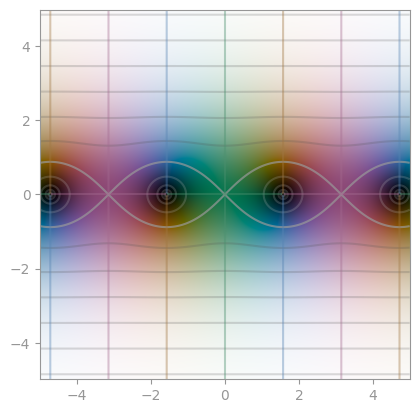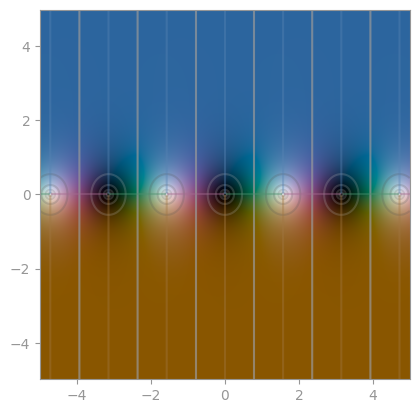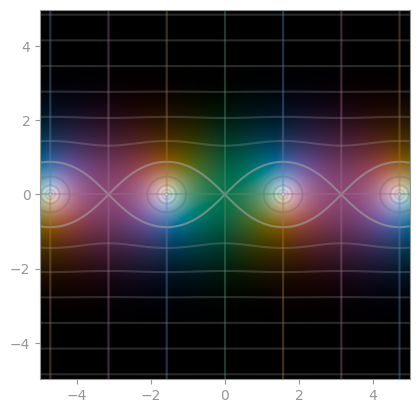
np.sin	np.cos	np.tan

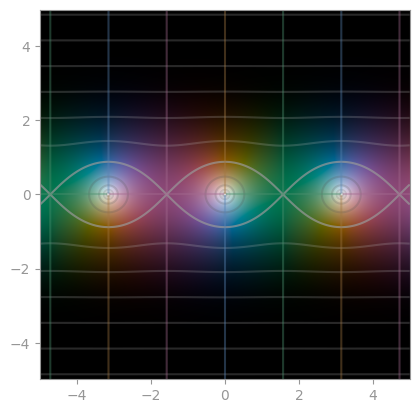
sec	csc	cot

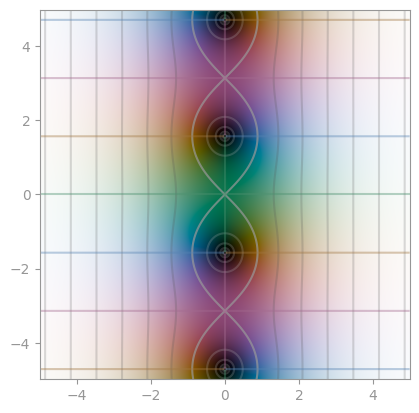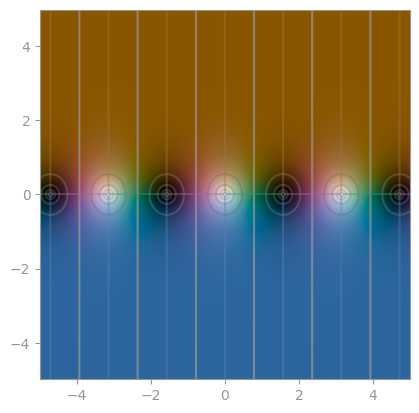
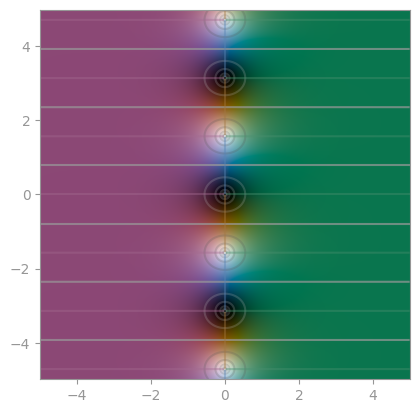
np.sinh	np.cosh	np.tanh

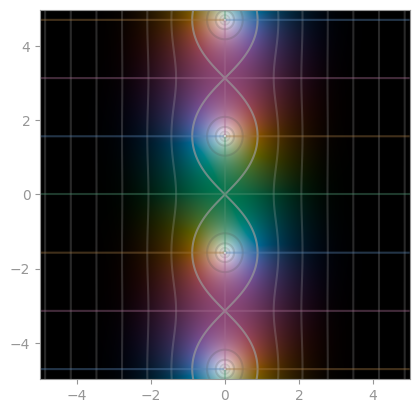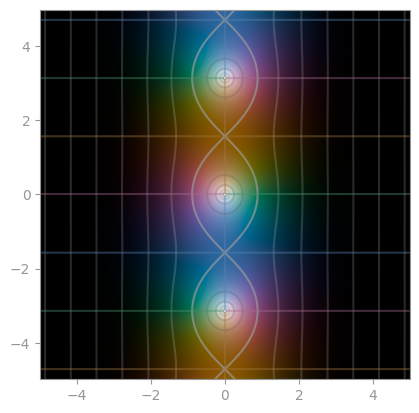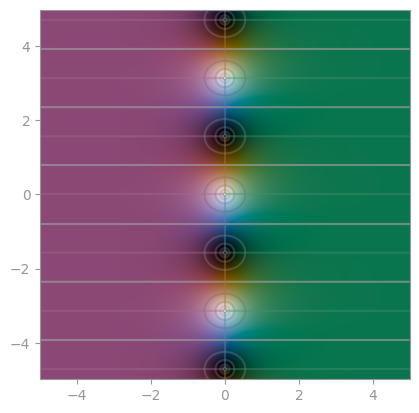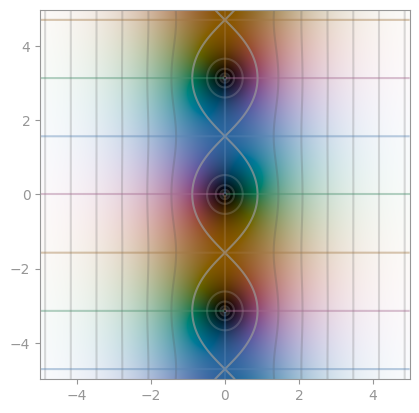
secans hyperbolicus	cosecans hyperbolicus	cotangent hyperbolicus

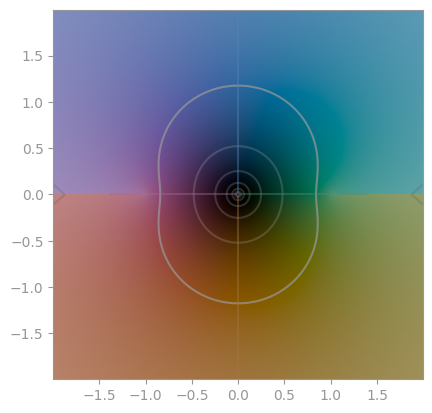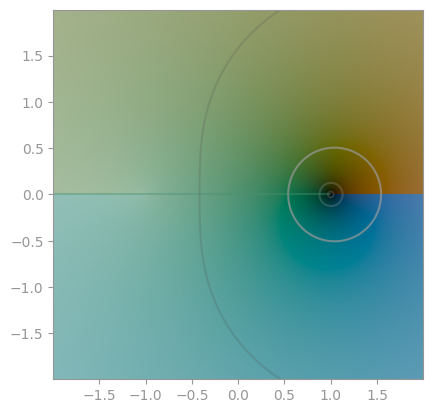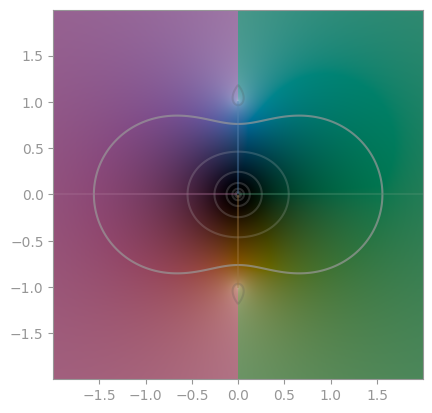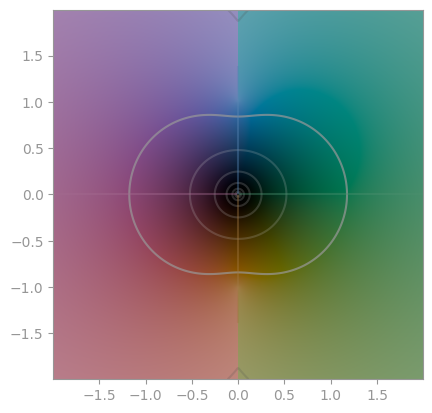
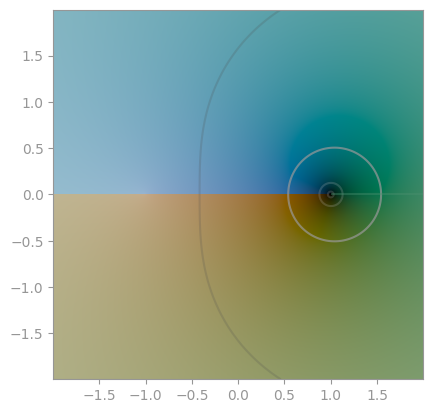
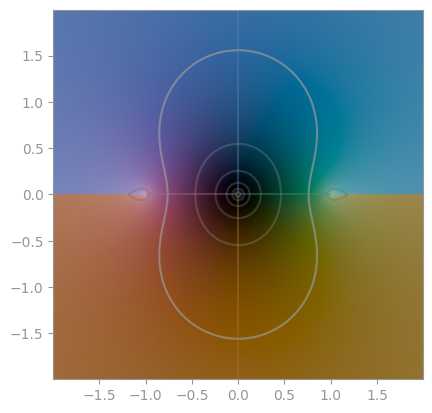
np.arcsin	np.arccos	np.arctan

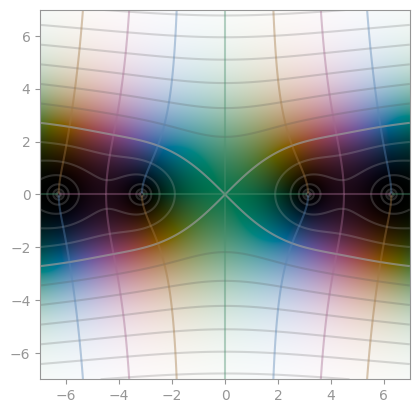
np.arcsinh	np.arccosh	np.arctanh

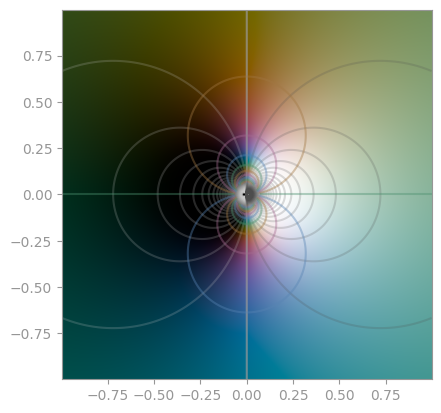
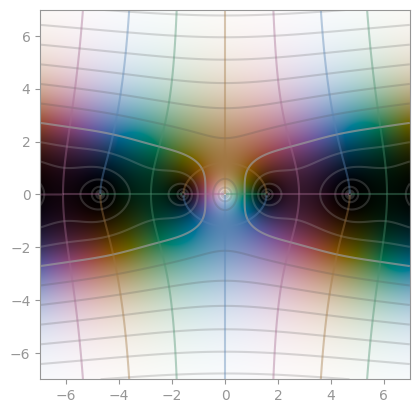
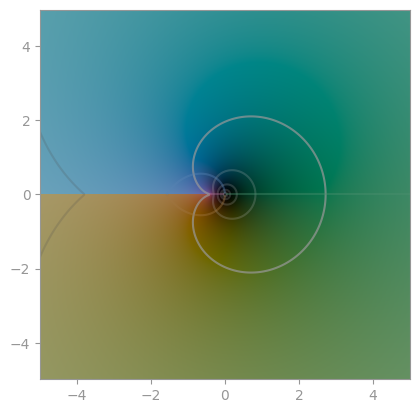
Sinc, sin(z) / z	cos(z) / z	tan(z) / z

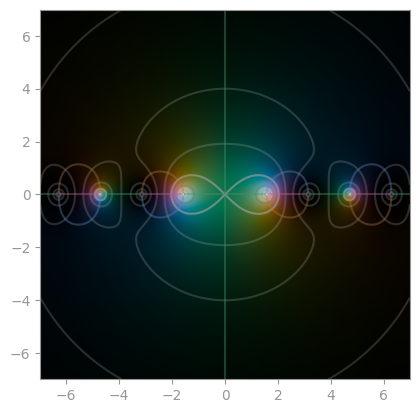
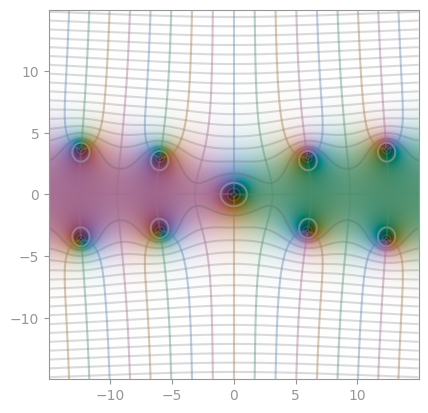
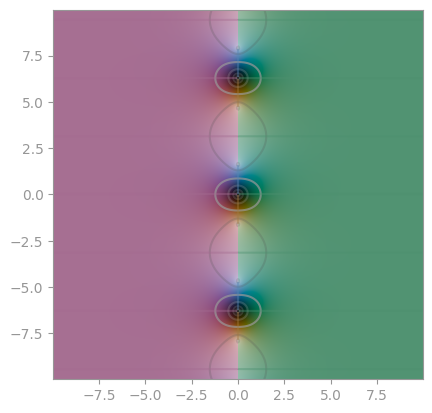
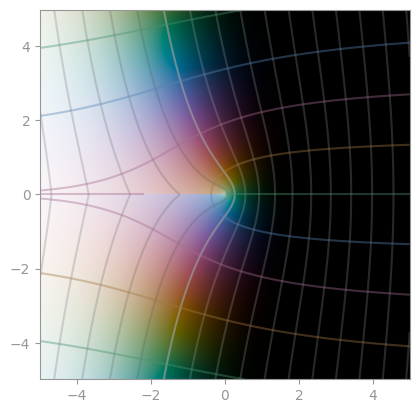
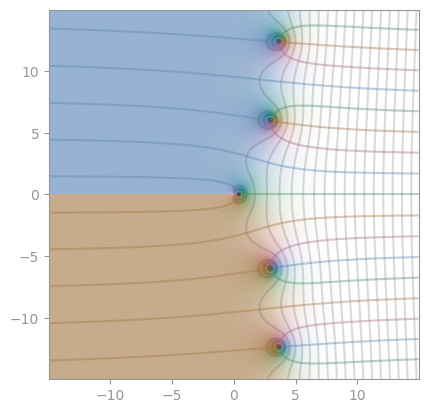
Integral sine Si	Integral cosine Ci	Lambert W function

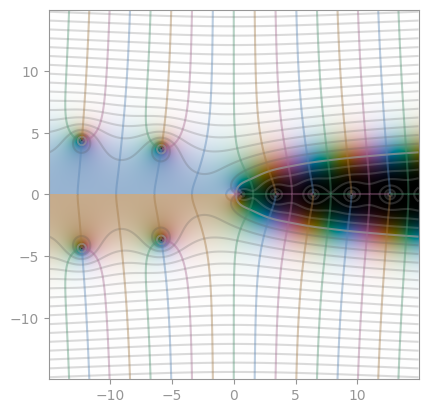
Gudermannian function	Exponential integral E1	Exponential integral Ei

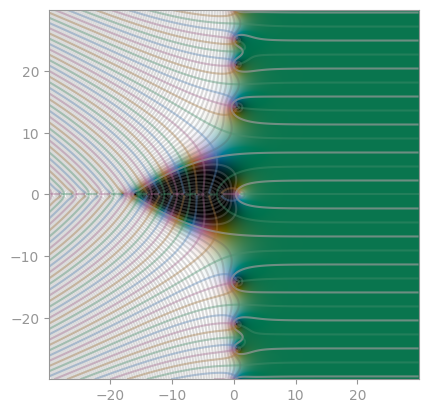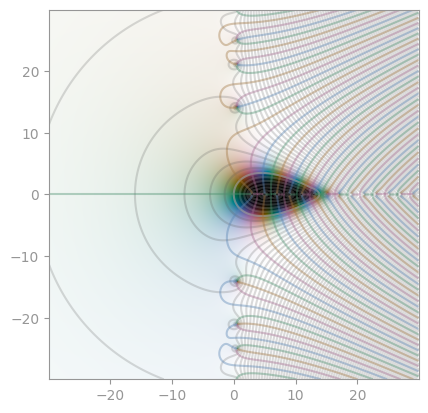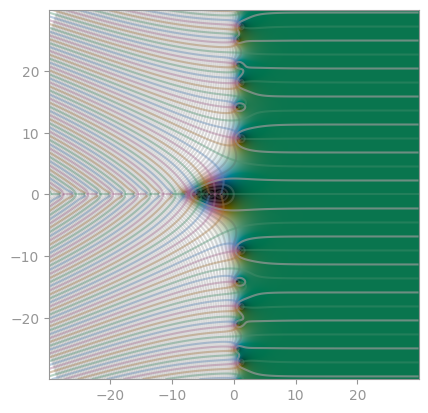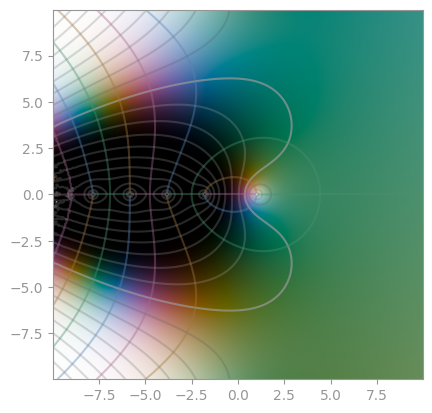
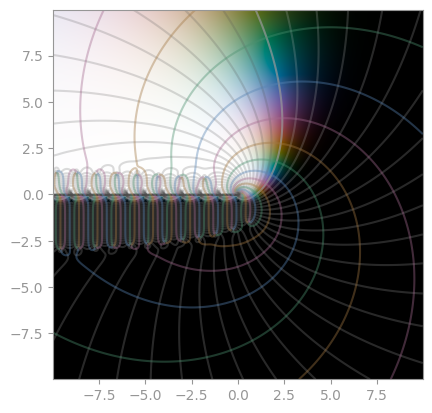
mpmath.zeta	Bernoulli function	Dirichlet eta function

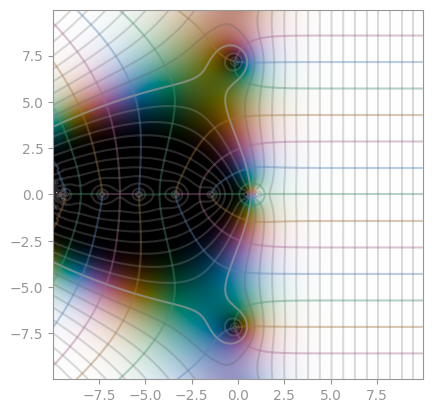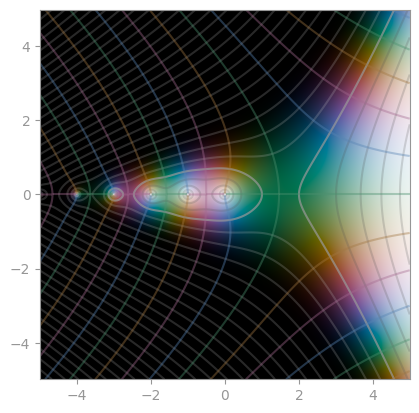
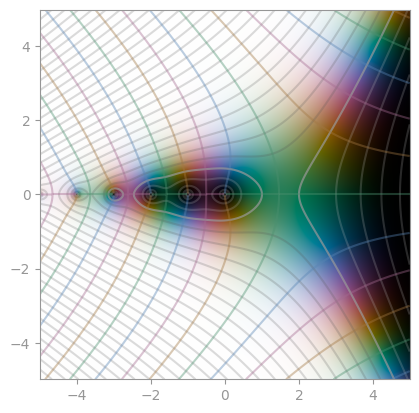
Hurwitz zeta function with a = 1/3	Hurwitz zeta function with a = 24/25	Hurwitz zeta function with s = 3 + 4i

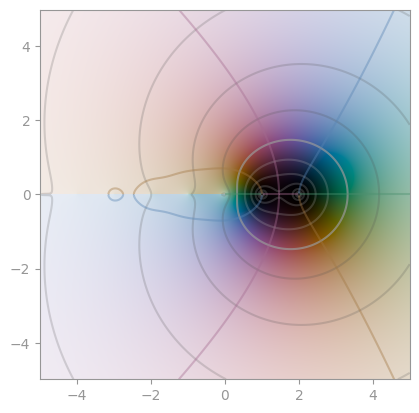
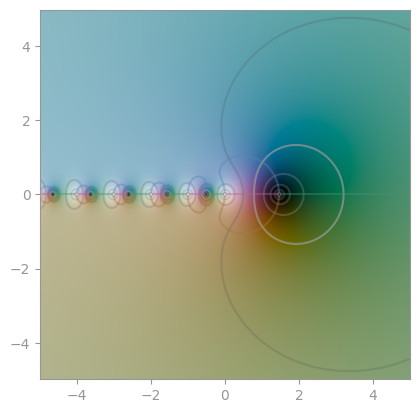
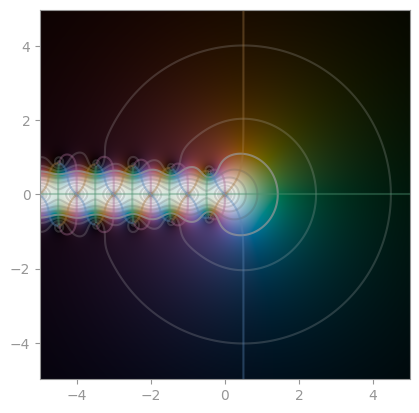
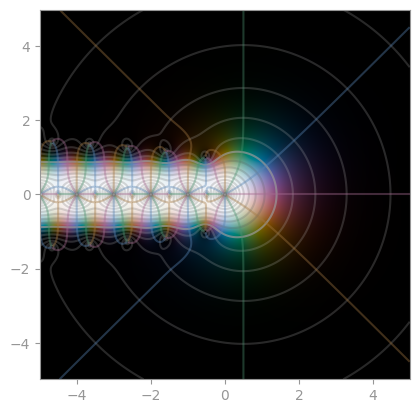
scipy.special.gamma	reciprocal Gamma	scipy.special.loggamma

scipy.special.digamma	Polygamma 1	Polygamma 2

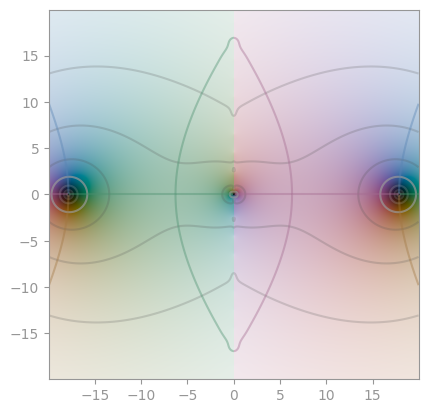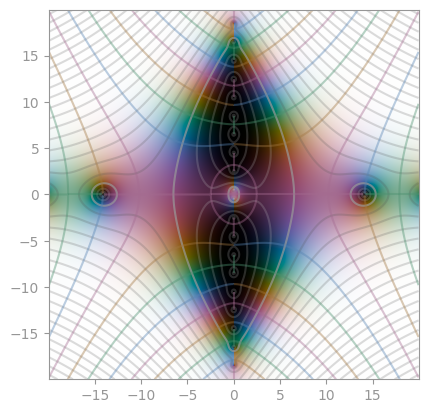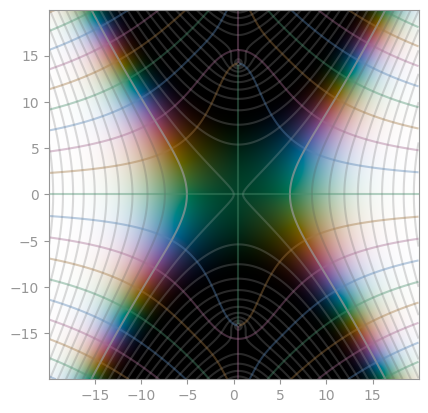Riemann-Siegel theta function	Z-function	Riemann-Xi

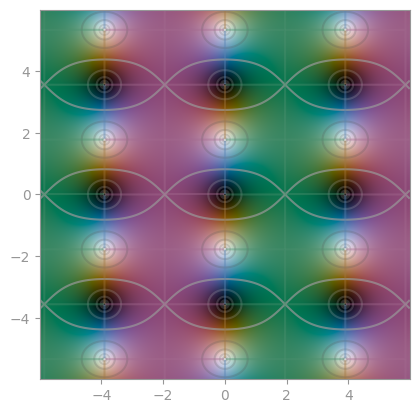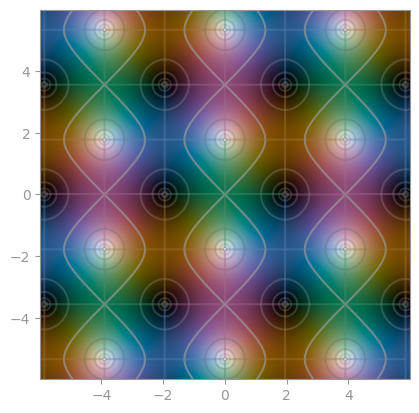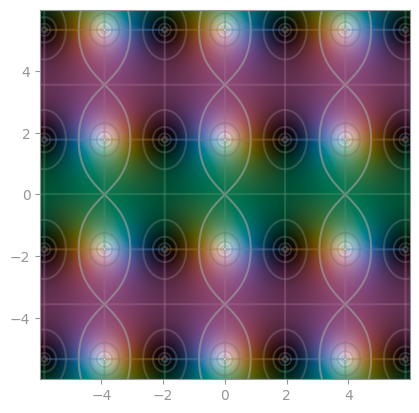Jacobi elliptic function sn(0.6)	cn(0.6)	dn(0.6)

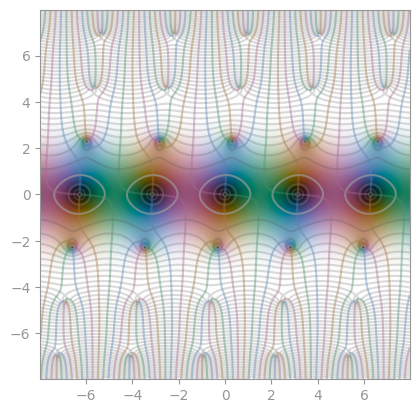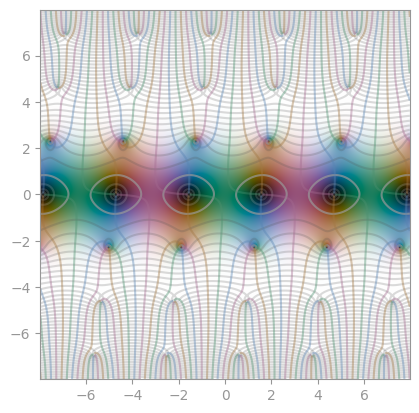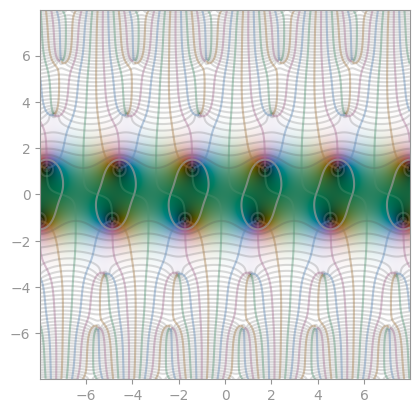Jacobi theta 1 with q=0.1 * exp(0.1j * np.pi))	Jacobi theta 2 with the same q	Jacobi theta 3 with the same q

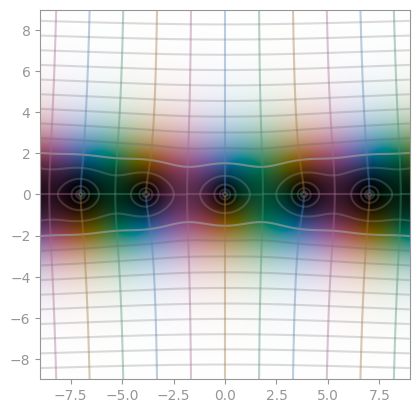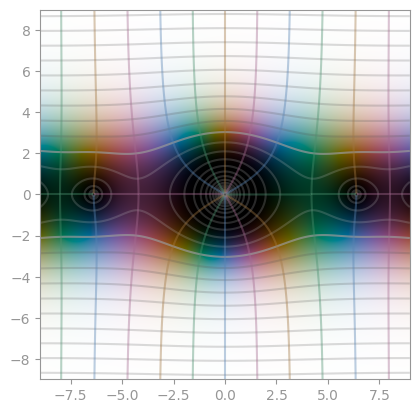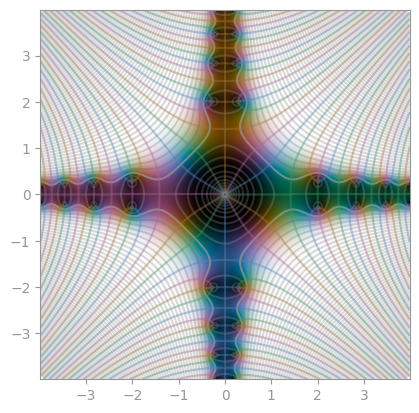
Bessel function, first kind, order 1	Bessel function, first kind, order 2	Bessel function, first kind, order 3

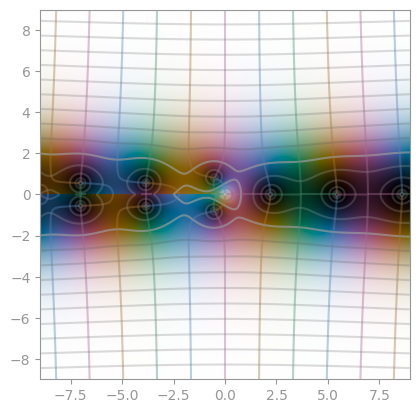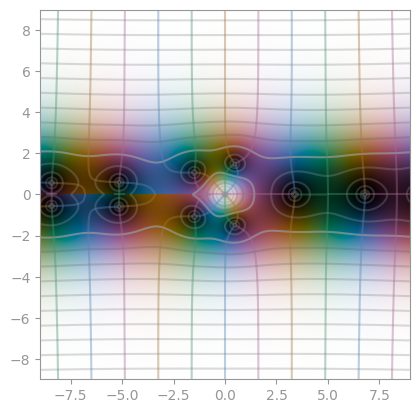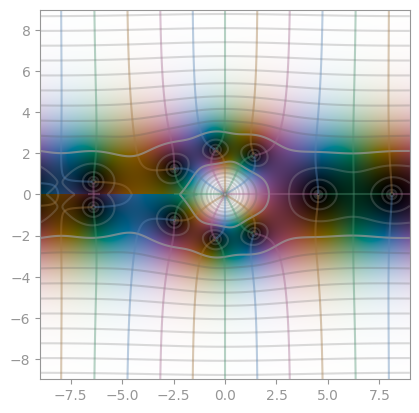
Bessel function, second kind, order 1	Bessel function, second kind, order 2	Bessel function, second kind, order 3

Hankel function of first kind (n=1.0)	Hankel function of first kind (n=3.1)	Hankel function of second kind (n=1.0)

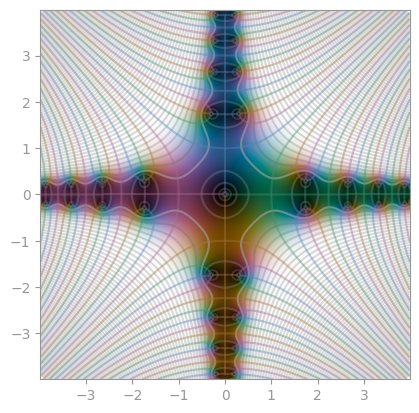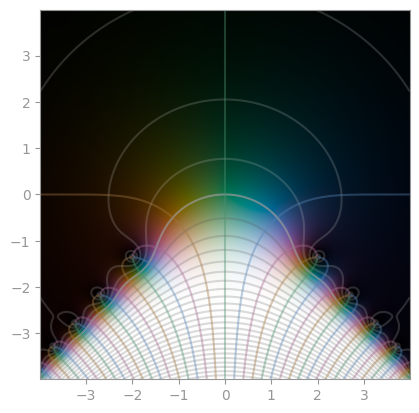Fresnel S	Fresnel C	Faddeeva function

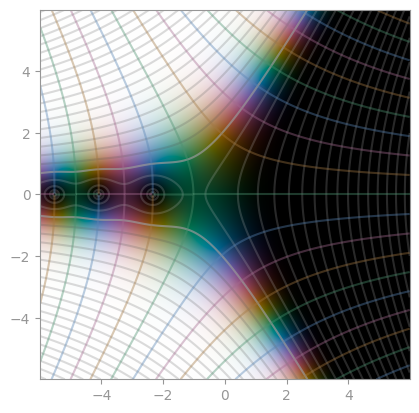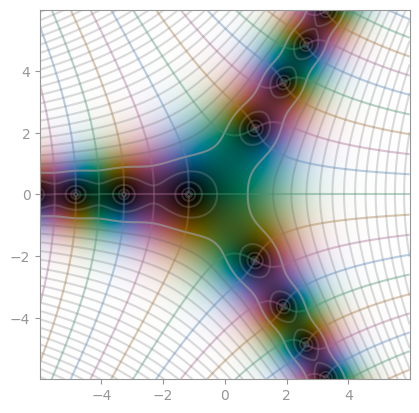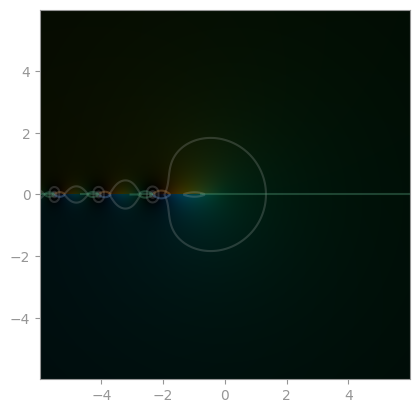
Airy function Ai	Bi	Exponentially scaled eAi

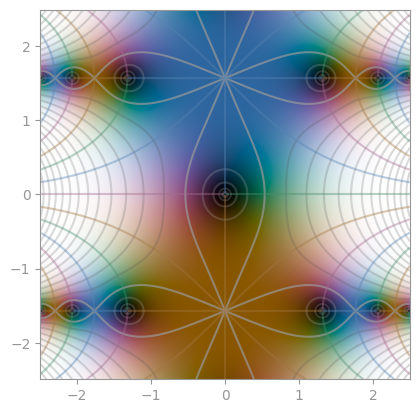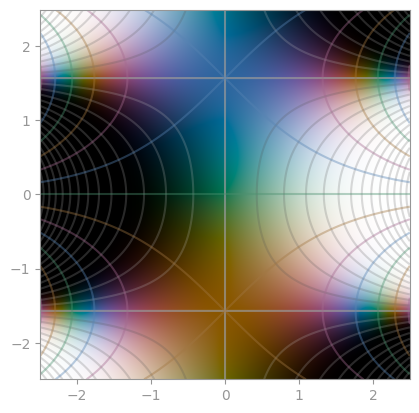tanh(pi / 2 * sinh(z))	sinh(pi / 2 * sinh(z))	exp(pi / 2 * sinh(z))

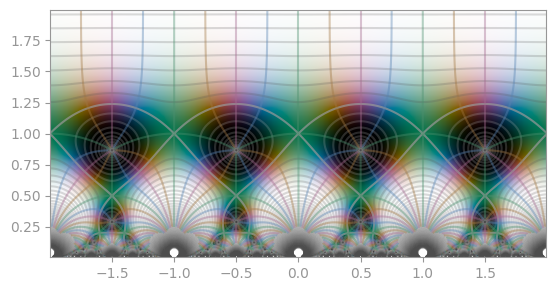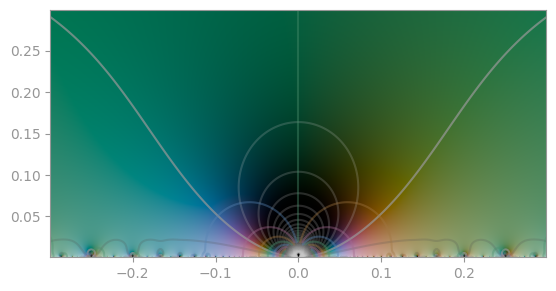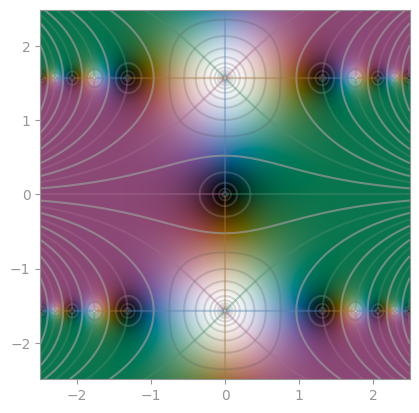
Klein's j-invariant	Dedekind eta function

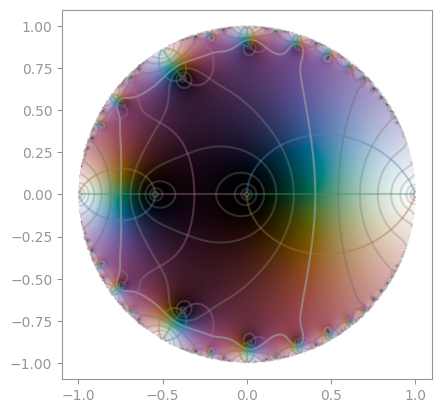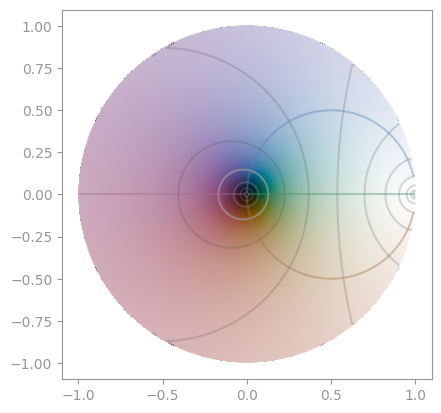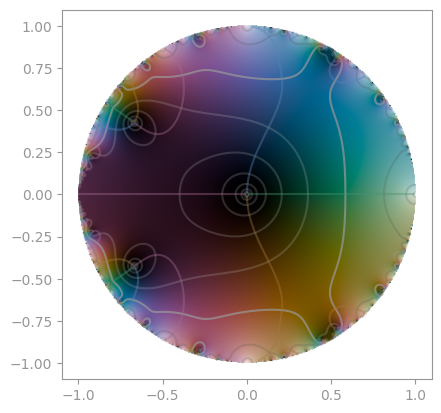Lambert series with 1s	Lambert series with von-Mangoldt-coefficients	Lambert series with Liouville-coefficients

Testing

To run the cplot unit tests, check out this repository and run

tox

Similar projects and further reading

• Tristan Needham, Visual Complex Analysis, 1997
• François Labelle, A Gallery of Complex Functions, 2002
• Douglas Arnold and Jonathan Rogness, Möbius transformations revealed, 2008
• Konstantin Poelke and Konrad Polthier, Lifted Domain Coloring, 2009
• Elias Wegert and Gunter Semmler, Phase Plots of Complex Functions: a Journey in Illustration, 2011
• Elias Wegert, Calendars Complex Beauties, 2011-
• Elias Wegert, Visual Complex Functions, 2012
• empet, Visualizing complex-valued functions with Matplotlib and Mayavi, Domain coloring method, 2014
• John D. Cook, Visualizing complex functions, 2017
• endolith, complex-colormap, 2017
• Anthony Hernandez, dcolor, 2017
• Juan Carlos Ponce Campuzano, DC gallery, 2018
• 3Blue1Brown, Winding numbers and domain coloring, 2018
• Ricky Reusser, Domain Coloring with Adaptive Contouring, 2019
• Ricky Reusser, Locally Scaled Domain Coloring, Part 1: Contour Plots, 2020
• David Lowry-Duda, Visualizing modular forms, 2020

License

This software is published under the GPL-3.0 license. In cases where the constraints of the GPL prevent you from using this software, feel free contact the author.