Graph algorithms in Cython
Welcome to our Python library for graph algorithms. The library includes both Dijkstra's and Bellman-Ford's algorithms, with plans to add more common path algorithms later. It is also open-source and easy to integrate with other Python libraries. To get started, simply install the library using pip, and import it into your Python project.
Documentation : https://edsger.readthedocs.io/en/latest/
To use Dijkstra's algorithm, you can import the Dijkstra class from the path module. The function takes a graph and a source node as input, and returns the shortest path from the source node to all other nodes in the graph.
import pandas as pd
from edsger.path import Dijkstra
# Create a DataFrame with the edges of the graph
edges = pd.DataFrame({
'tail': [0, 0, 1, 2, 2, 3],
'head': [1, 2, 2, 3, 4, 4],
'weight': [1, 4, 2, 1.5, 3, 1]
})
edges| tail | head | weight | |
|---|---|---|---|
| 0 | 0 | 1 | 1.0 |
| 1 | 0 | 2 | 4.0 |
| 2 | 1 | 2 | 2.0 |
| 3 | 2 | 3 | 1.5 |
| 4 | 2 | 4 | 3.0 |
| 5 | 3 | 4 | 1.0 |
# Initialize the Dijkstra object
dijkstra = Dijkstra(edges)
# Run the algorithm from a source vertex
shortest_paths = dijkstra.run(vertex_idx=0)
print("Shortest paths:", shortest_paths)Shortest paths: [0. 1. 3. 4.5 5.5]
We get the shortest paths from the source node 0 to all other nodes in the graph. The output is an array with the shortest path length to each node. A path length is the sum of the weights of the edges in the path.
The Bellman-Ford algorithm can handle graphs with negative edge weights and detect negative cycles, making it suitable for more complex scenarios than Dijkstra's algorithm.
from edsger.path import BellmanFord
# Create a graph with negative weights
edges_negative = pd.DataFrame({
'tail': [0, 0, 1, 1, 2, 3],
'head': [1, 2, 2, 3, 3, 4],
'weight': [1, 4, -2, 5, 1, 3] # Note the negative weight
})
edges_negative| tail | head | weight | |
|---|---|---|---|
| 0 | 0 | 1 | 1.0 |
| 1 | 0 | 2 | 4.0 |
| 2 | 1 | 2 | -2.0 |
| 3 | 1 | 3 | 5.0 |
| 4 | 2 | 3 | 1.0 |
| 5 | 3 | 4 | 3.0 |
# Initialize and run Bellman-Ford
bf = BellmanFord(edges_negative)
shortest_paths = bf.run(vertex_idx=0)
print("Shortest paths:", shortest_paths)Shortest paths: [ 0. 1. -1. 0. 3.]
The Bellman-Ford algorithm finds the optimal path even with negative weights. In this example, the shortest path from node 0 to node 2 has length -1 (going 0→1→2 with weights 1 + (-2) = -1), which is shorter than the direct path 0→2 with weight 4.
Bellman-Ford can also detect negative cycles, which indicate that no shortest path exists:
# Create a graph with a negative cycle
edges_cycle = pd.DataFrame({
'tail': [0, 1, 2],
'head': [1, 2, 0],
'weight': [1, -2, -1] # Cycle 0→1→2→0 has total weight -2
})
bf_cycle = BellmanFord(edges_cycle)
try:
bf_cycle.run(vertex_idx=0)
except ValueError as e:
print("Error:", e)Error: Negative cycle detected in the graph
The BFS (Breadth-First Search) algorithm finds shortest paths in directed graphs where edge weights are ignored (or all edges are treated as having equal weight). It's particularly efficient for finding paths based on the minimum number of hops/edges rather than weighted distances.
from edsger.path import BFS
# Create an unweighted directed graph
edges_unweighted = pd.DataFrame({
'tail': [0, 0, 1, 2, 2, 3],
'head': [1, 2, 3, 3, 4, 4]
})
edges_unweighted| tail | head | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 2 |
| 2 | 1 | 3 |
| 3 | 2 | 3 |
| 4 | 2 | 4 |
| 5 | 3 | 4 |
# Initialize BFS
bfs = BFS(edges_unweighted)
# Run BFS from vertex 0 with path tracking
predecessors = bfs.run(vertex_idx=0, path_tracking=True)
print("Predecessors:", predecessors)
# Extract the path to vertex 4
path = bfs.get_path(4)
print("Path from 0 to 4:", path)Predecessors: [-9999 0 0 1 2]
Path from 0 to 4: [4 2 0]
The BFS algorithm is ideal for directed graphs when:
- All edges should be treated equally (ignoring edge weights)
- You need to find paths with the minimum number of edges/hops
- You want the fastest path-finding algorithm for unweighted directed graphs (O(V + E) time complexity)
Note: The predecessor value -9999 indicates either the start vertex or an unreachable vertex. In the path output, vertices are listed from target to source.
pip install edsgerFor development work, clone the repository and install in development mode:
git clone https://github.com/aetperf/Edsger.git
cd Edsger
pip install -r requirements-dev.txt
pip install -e .This project uses several development tools to ensure code quality:
We use Pyright for static type checking:
# Run type checking
make typecheck
# Or directly with pyright
pyrightFor more details on type checking configuration and gradual typing strategy, see TYPING.md.
# Run all tests
make test
# Run with coverage
make coverage# Format code with black
make format
# Check code style
make lintThis project uses pre-commit hooks to maintain code quality. The hooks behave differently based on the branch:
- Protected branches (main, release)*: All hooks run including pyright type checking
- Feature branches: Only formatting hooks run (black, cython-lint) for faster commits
- Run
make typecheckorpre-commit run --all-filesto manually check types before merging
- Run
# Install pre-commit hooks
pre-commit install
# Run all hooks manually
pre-commit run --all-files
# Skip specific hooks if needed
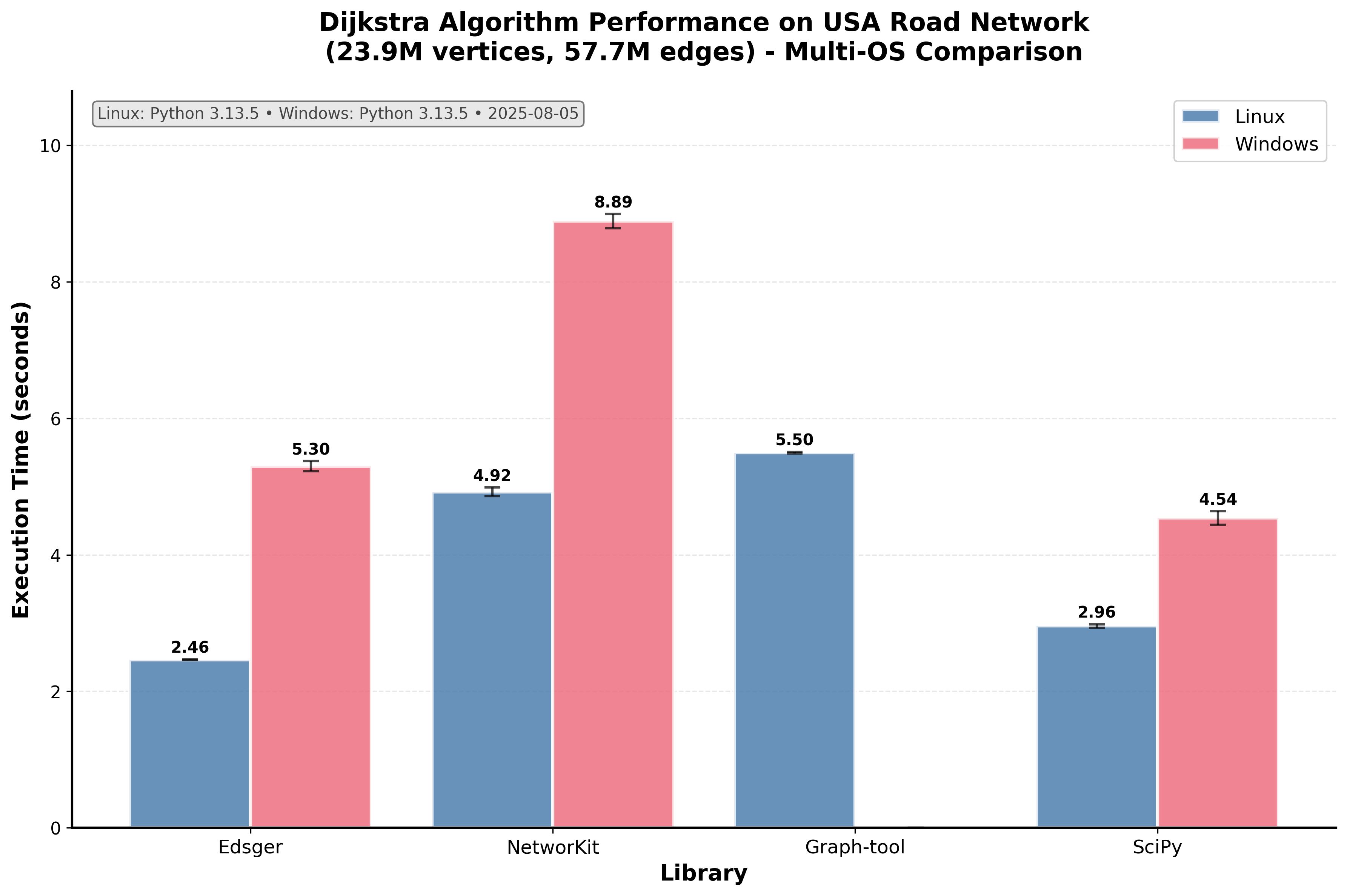
SKIP=pyright git commit -m "your message"make help # Show all available commandsEdsger is designed to be dataframe-friendly, providing seamless integration with pandas workflows for graph algorithms. Also it is rather efficient on Linux. Our benchmarks on the USA road network (23.9M vertices, 57.7M edges) demonstrate nice performance:
We welcome contributions to the Edsger library. If you have any suggestions, bug reports, or feature requests, please open an issue on our GitHub repository.
Edsger is licensed under the MIT License. See the LICENSE file for more details.
For any questions or inquiries, please contact me at francois.pacull@architecture-performance.fr.