Release The Region Update · ZibraMax/FEM

A Python FEM implementation.

N dimensional FEM implementation for M variables per node problems.

Installation

Use the package manager pip to install AFEM.

pip install AFEM

Contributing

Pull requests are welcome. For major changes, please open an issue first to discuss what you would like to change.

Please make sure to update tests as appropriate.

Full Docs

Tutorial

Using pre implemented equations

Avaliable equations:

1D 1 Variable ordinary diferential equation
1D 1 Variable 1D Heat with convective border
1D 2 Variable Euler Bernoulli Beams
1D 3 Variable Non-linear Euler Bernoulli Beams
2D 1 Variable Torsion
2D 1 Variable Poisson equation
2D 1 Variable second order PDE
2D 1 Variable 2D Heat with convective borders
2D 2 Variable Plane Strees
2D 2 Variable Plane Strees Orthotropic
2D 2 Variable Plane Strain
3D 3 variables per node isotropic elasticity

Numerical Validation:

1D 1 Variable ordinary diferential equation
1D 1 Variable 1D Heat with convective border
1D 2 Variable Euler Bernoulli Beams
1D 3 Variable Non-linear Euler Bernoulli Beams
2D 1 Variable Torsion
2D 1 Variable 2D Heat with convective borders
2D 2 Variable Plane Strees
2D 2 Variable Plane Strain

Steps:

Create geometry
Create Border Conditions (Point and regions supported)
Solve!
For example: Example 2, Example 5, Example 11-14

Example without geometry file (Test 2):

import matplotlib.pyplot as plt #Import libraries
from FEM.Torsion2D import Torsion2D #import AFEM Torsion class
from FEM.Geometry import Delaunay #Import Meshing tools

#Define some variables with geometric properties
a = 0.3
b = 0.3
tw = 0.05
tf = 0.05

#Define material constants
E = 200000
v = 0.27
G = E / (2 * (1 + v))
phi = 1 #Rotation angle

#Define domain coordinates
vertices = [
        [0, 0],
        [a, 0],
        [a, tf],
        [a / 2 + tw / 2, tf],
        [a / 2 + tw / 2, tf + b],
        [a, tf + b],
        [a, 2 * tf + b],
        [0, 2 * tf + b],
        [0, tf + b],
        [a / 2 - tw / 2, tf + b],
        [a / 2 - tw / 2, tf],
        [0, tf],
]

#Define triangulation parameters with `_strdelaunay` method.
params = Delaunay._strdelaunay(constrained=True, delaunay=True,
                                                                        a='0.00003', o=2)
#**Create** geometry using triangulation parameters. Geometry can be imported from .msh files.
geometry = Delaunay(vertices, params)

#Save geometry to .json file
geometry.exportJSON('I_test.json')

#Create torsional 2D analysis.
O = Torsion2D(geometry, G, phi)
#Solve the equation in domain.
#Post process and show results
O.solve()
plt.show()

Example with geometry file (Example 2):

import matplotlib.pyplot as plt #Import libraries
from FEM.Torsion2D import Torsion2D #import AFEM
from FEM.Geometry import Geometry #Import Geometry tools

#Define material constants.
E = 200000
v = 0.27
G = E / (2 * (1 + v))
phi = 1 #Rotation angle

#Load geometry with file.
geometry = Geometry.importJSON('I_test.json')

#Create torsional 2D analysis.
O = Torsion2D(geometry, G, phi)
#Solve the equation in domain.
#Post process and show results
O.solve()
plt.show()

Creating equation classes

Note: Don't forget the docstring!

Steps

Create a Python flie and import the libraries:
```
from .Core import *
from tqdm import tqdm
import numpy as np
import matplotlib.pyplot as plt
```
- Core: Solver
- Numpy: Numpy data
- Matplotlib: Matplotlib graphs
- Tqdm: Progressbars

Create a Python class with Core inheritance

class PlaneStress(Core):
    def __init__(self,geometry,*args,**kargs):
    #Do stuff
    Core.__init__(self,geometry)

It is important to manage the number of variables per node in the input geometry.

Define the matrix calculation methods and post porcessing methods.
```
def elementMatrices(self):
def postProcess(self):
```

The elementMatrices method uses gauss integration points, so you must use the following structure:

for e in tqdm(self.elements,unit='Element'):
    _x,_p = e.T(e.Z.T) #Gauss points in global coordinates and Shape functions evaluated in gauss points
    jac,dpz = e.J(e.Z.T) #Jacobian evaluated in gauss points and shape functions derivatives in natural coordinates
    detjac = np.linalg.det(jac)
    _j = np.linalg.inv(jac) #Jacobian inverse
    dpx = _j @ dpz #Shape function derivatives in global coordinates
    for k in range(len(e.Z)): #Iterate over gauss points on domain
        #Calculate matrices with any finite element model
    #Assign matrices to element

A good example is the PlaneStress class in the Elasticity2D.py file.

Roadmap

2D elastic plate theory
Transient analysis (Core modification)
Non-Lineal for 2D equation (All cases)
Testing and numerical validation (WIP)

Example index:

Example 1: Preliminar geometry test
Example 2: 2D Torsion 1 variable per node. H section-Triangular Quadratic.
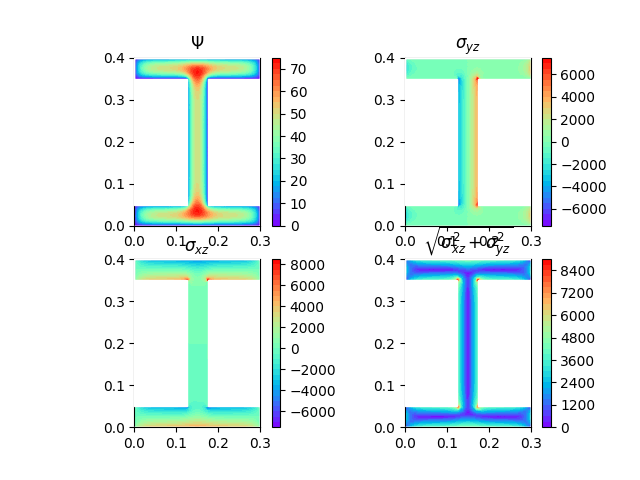
Example 3: 2D Torsion 1 variable per node. Square section-Triangular Quadratic.
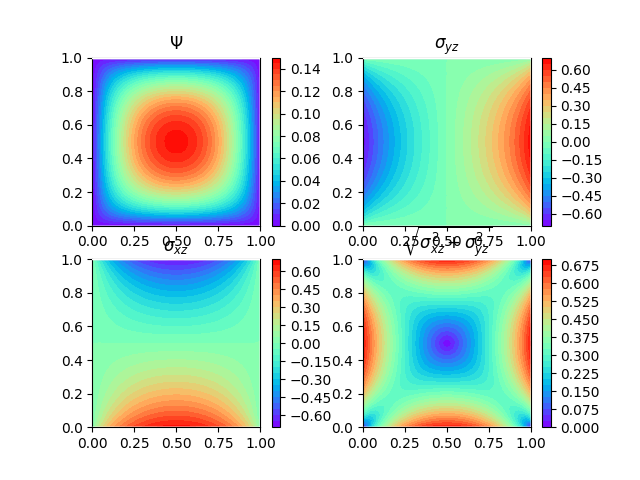
Example 4: 2D Torsion 1 variable per node. Mesh from internet-Square Lineal.
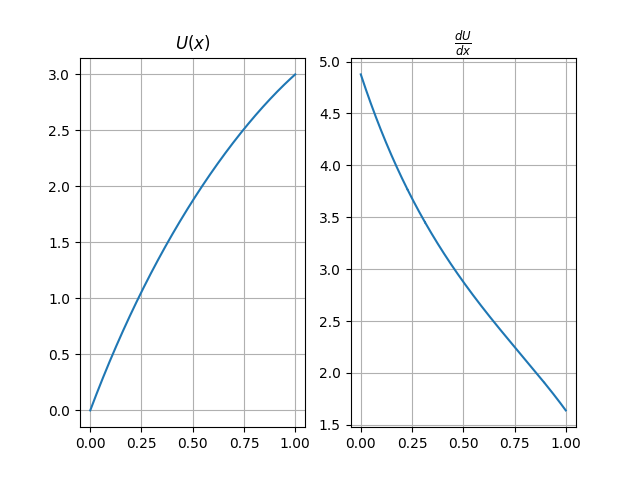
Example 5: 2D Torsion 1 variable per node. Creating and saving mesh-Triangular Quadratic.
Example 6: 1D random differential equation 1 variable per node. Linear Quadratic.
Example 7: GiD Mesh import test — Serendipity elements
Example 8: Plane Stress 2 variable per node. Plate in tension — Serendipity.
Example 9: Plane Stress 2 variable per node. Simple Supported Beam — Serendipity.
Example 10: Plane Stress 2 variable per node. Cantilever Beam — Triangular Quadratic.
Example 11: Plane Stress 2 variable per node. Fixed-Fixed Beam — Serendipity.
Example 12: Plane Strain 2 variable per node. Embankment from GiD — Serendipity.
Example 13: Plane Strain 2 variable per node. Embankment — Triangular Quadratic.
Example 14: Plane Stress 2 variable per node. Cantilever Beam — Serendipity.
Example 15: Profile creation tool. Same as Example 14
Example 16: Non-Local Plane Stress. [WIP]
Example 17: 1D Heat transfer.
Example 18: 2D border elements creation.
Example 19: Apply loads on regions. loadOnRegion method on Test 11
Example 20: Reddy's Example 11.7.1 Ed 3
Example 21: Example 20 with serendipity elements.
Example 22: Example 20 with refined mesh.
Example 23: Reddy's Problem 11.1 Ed 3 Plain Strain
Example 24: Example 23 with refined mesh
Example 25: Holes concept. With Example 24
Example 26: Fillets concept.
Example 27: Combination of Holes Fillets, Plane Stress
Example 28: Fillets and Holes mesh files of Example 27
Example 29: Fillets and Holes in Example 13
Example 30: Border conditions and loads in holes
Example 31: 2D Heat with convective borders
Example 32: Border conditions and loads in holes
Example 33: Example 30 with Heat
Example 34: Custom plots, Beam-Girder steel plate connection
Example 35: Torsion with fillets
Example 36: Convective Heat Transfer from Samson-Mano's software
Example 37: Convective Heat Transfer from Samson-Mano's software
Example 38: Elements with different properties: Torsion with holes
Example 37: Elements with different properties: Torsion with holes Symetrical
Example 38 & 39: Polar moment of inertia for hollow sections
Example 40 & 41: Euler Bernoulli beams, linear and non-linear
Example 42: Non-linear equation solver test
Example 43: Orthotripic plane stress
Example 44: MeshingNet data creation code

References

J. N. Reddy. Introduction to the Finite Element Method, Third Edition (McGraw-Hill Education: New York, Chicago, San Francisco, Athens, London, Madrid, Mexico City, Milan, New Delhi, Singapore, Sydney, Toronto, 2006). https://www.accessengineeringlibrary.com/content/book/9780072466850

Jonathan Richard Shewchuk, (1996) Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator

Ramirez, F. (2020). ICYA 4414 Modelación con Elementos Finitos [Class handout]. Universidad de Los Andes.

License

MIT

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

The Region Update