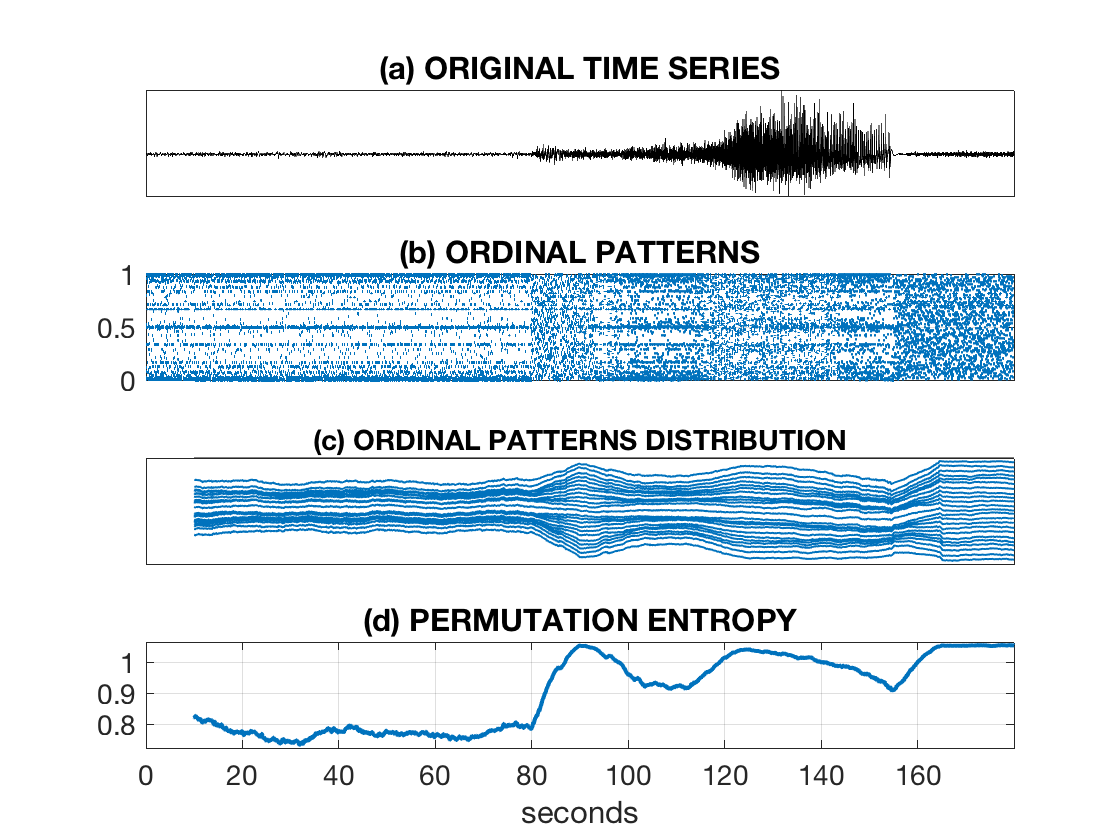
The OPA (ordinal-patterns-analysis) toolbox is intended for nonlinear analysis of multivariate time series with becoming more and more popular ordinal-patterns-based measures [1-5] which are efficiently computed [6,7] and visualized:
- permutation entropy (cfg.method = 'PE') [2]
- permutation entropy for ordinal patterns with tied ranks (cfg.method = 'eqPE') [4,8]
- permutation entropy and ordinal patterns distributions (cfg.method = 'opdPE') [3]
- conditional entropy of ordinal patterns (cfg.method = 'cePE') [6]
- robust permutation entropy (cfg.method = 'rePE') [4,7]
- new ordinal-patterns-based measures are to be added (your suggestions and feedback are welcome!)
INPUT
The interface of OPA toolbox is provided by a function outdata = OPanalysis( cfg, indata ), where
- cfg is a configuration structure with method's parameters;
- indata is data to be analyzed.
OUTPUT
- outdata - computed values of ordinal-patterns-based complexity measure
CITING THE CODE
[a] Unakafova, Valentina (2017). Ordinal-patterns-based analysis (beta-version) (www.mathworks.com/matlabcentral/fileexchange/63782-ordinal-patterns-based-analysis--beta-version-), MATLAB Central File Exchange. Retrieved Month Day, Year.
[b] Unakafova, V.A., Keller, K., 2013. Efficiently measuring complexity on the basis of real-world data. Entropy, 15(10), 4392-4415.
EXAMPLE OF USE (see more examples for different methods and parameters in examples.m and OPanalysis.m help):
cfg = [];
cfg.method = 'opdPE'; % try also 'PE', 'CE', 'rePE' and 'all' here
cfg.order = 3; % for ordinal pattens of order 3 (4-points ordinal patterns)
cfg.delay = 1; % for delay 1 between points in ordinal patterns (successive points)
cfg.windowSize = 512; % for window size 512 in time points
indata = rand( 1, 7777 );
for i = 4000:7000 % change of data complexity
indata( i ) = 4 * indata( i - 1 ) * ( 1 - indata( i - 1 ) );
end
outdata = OPanalysis( cfg, indata );
FOLDERS DESCRIPTION
examples.m script contains examples of using OPA toolbox for different ordinal-patterns-based measures with different parameters
The Code folder contains functions for computing the aforementioned ordinal-patterns-based measures.
The Data folder contains example epileptic EEG datasets from https://vis.caltech.edu/~rodri/data.htm
(dataset 5, 130-2_c4.asc) used for illustrating in examples.m.
The Tables folder contain precomputed tables as *.mat-files for efficient computing of ordinal-patterns-based methods.
NOTES:
Please, see www.mathworks.com/matlabcentral/fileexchange/44161-permutation-entropy--fast-algorithm- for some discussion of parameters choice. Values of ordinal-patterns-based measures are computed in maximally overlapping sliding windows in a fast way [6,7]. This is a beta-version of OPA-toolbox, new ordinal-patterns-based measures are to be added (your feedback and comments are welcome)!
REFERENCES:
[1] Amigo, J.M., Keller, K. and Unakafova, V.A., 2015. On entropy, entropy-like quantities, and applications. Discrete & Continuous Dynamical Systems-Series B, 20(10).
[2] Bandt C., Pompe B., Permutation entropy: a natural complexity measure for time series. Physical review letters, 2002, APS
[3] Keller, K., and M. Sinn. Ordinal analysis of time series. Physica A: Statistical Mechanics and its Applications 356.1 (2005): 114--120
[4] Keller, K., Unakafov, A.M. and Unakafova, V.A., 2014. Ordinal patterns, entropy, and EEG. Entropy, 16(12), pp.6212-6239.
[5] Zanin, M., Zunino, L., Rosso, O.A. and Papo, D., 2012. Permutation entropy and its main biomedical and econophysics applications: a review. Entropy, 14(8), pp.1553-1577.
[6] Unakafova, V.A., Keller, K., 2013. Efficiently measuring complexity on the basis of real-world Data. Entropy, 15(10), 4392-4415.
[7] Unakafova, V.A., 2015. Investigating measures of complexity for dynamical systems and for time series (Doctoral dissertation, University of Luebeck).
[8] Bian, C., Qin, C., Ma, Q.D. and Shen, Q., 2012. Modified permutation-entropy analysis of heartbeat dynamics. Physical Review E, 85(2), p.021906.
[9] Amigo, J.M., Zambrano, S. and Sanjuan, M.A., 2008. Combinatorial detection of determinism in noisy time series. EPL (Europhysics Letters), 83(6), p.60005.
[10] Cao, Y., Tung, W.W., Gao, J.B. et al., 2004. Detecting dynamical changes in time series using the permutation entropy. Physical Review E, 70(4), p.046217.
[11] Riedl, M., Muller, A. and Wessel, N., 2013. Practical considerations of permutation entropy. The European Physical Journal Special Topics, 222(2), pp.249-262.