This is an implementation of priority queue operations with a Fibonacci heap. The amortized running time of Fibonacci heaps is better than with many other priority queue data structures. But the memory overhead per node is relatively large. The elements of the heap are key-value pairs. Note that this implementation is a min-heap, which means a higher priority is achieved with a lower key.
Fibonacci heaps have very good amortized running times. But for very small queues Fibonacci heaps are usually slower than other data structures. The reason for this are the high constant factors in the running time. Fibonacci heaps are better for large queues with a lot of elements. For n as the total number of elements in the heap:
| Operation | Amortized | Worst case |
|---|---|---|
| Space | O(n) | O(n) |
| Insert | O(1) | O(1) |
| Delete-Min | O(log n) | O(n) |
| Find-Min | O(1) | O(1) |
| Decrease-key | O(n) | O(n) |
| Merge | O(1) | O(1) |
The decrease-key operation for a node has an amortized runtime of O(1). The problem is that this performance can only be achieved when the target node is already known. In general this is not the case for a given value. In this implementation the node must be found before its key can be decreased. Searching in unordered data results in a linear runtime. It is possible to go around this problem by returning the node that was created by the insert function and use the node pointer as an input for the decrease-key function. This method is not used here because the node encapsulation was preferred over the better performance.
Two Fibonacci heaps are merged by the concatenation of their rootlists and a min pointer update. As a result, the runtime of merging is constant. The problem with this method is that changes made to one of the "sub-heaps" will also affect the merged heap. This may cause problems when the user of the heap is not aware of this side-effect. To prevent this situation the second heap will be set to an empty heap. With this reset, a crash would occur instead of an unwanted side-effect. When the user is aware of this effect the reset of the second heap can be omitted for better performance.
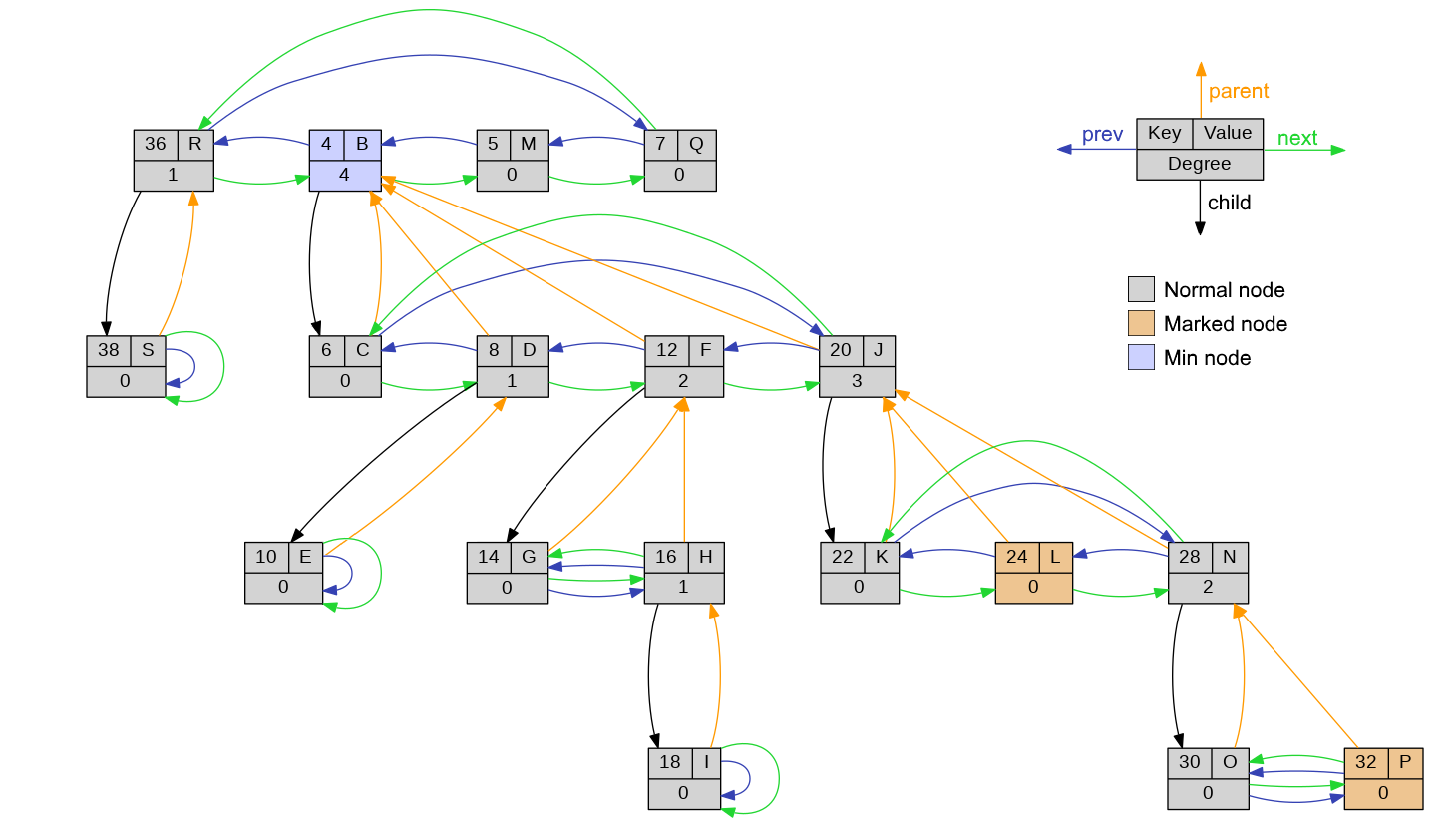
The concrete situation of the data structure can be visualized with the dump function. The dump will generate a graph
and png file with the Graphviz-Tool. This can be useful for a better understanding of the data structure and for
debugging purposes. Example of the Fibonacci heap visualization:
The getMin and extractMin functions return a value of type V. When the heap is empty zero will be returned. It would be safer to return an optional but that would cost memory and performance. This implementation preferred the better performance over type-safety. You can call the isEmpty-check before calling getMin or extractMin to avoid a situation where no minimum exists that can be returned.
This implementation allows using arbitrary types for the key-value pair. The key type has to provide the less and greater operator to order the heap. Usually it makes sense to use integer as the key type. Some functions use the equal operator on the value type in order to find the node of specific values.