Jan 07,2023/ by 李韋杰、胡芯瑋、鄭澤賢
- Motivation and Background
- Methodology
- Problem Definition
- Solution
- Experiment
- Conclusion
- Reference
Nowadays, environmental pollution and road congestion problems are getting increasingly worse, especially in densely populated areas. If using carpooling services, we can reduce the amount of carbon dioxide emitted by each car. Furthermore, cutting down the cost of travel for each passenger and increasing passenger satisfaction with shorter waiting time are also the advantages of carpooling services.
Here, we are going to use Reinforcement Learning to simulate the carpooling problem.
Our carpooling problem is not going to address problem of scheduling a fleet of taxis, but provide user(passenger) a option to choose a taxi which can let user has the shortest waiting time.
RL is known as a semi-supervised learning model in machine learning which enables an agent to learn in an interactive environment by trial and error using feedback from its own actions and experiences.
Unlike supervised learning where the feedback provided to the agent is correct set of actions for performing a task, RL uses rewards and punishments as signals for positive and negative behavior. Thus, its goal is to find a suitable action model that would maximize the total cumulative reward of the agent.
Q-learning is a model-free reinforcement learning algorithm to learn the value of an action in a particular state.
In Q-learning, the experience learned by the agent is stored in the Q table, and the value in the table expresses the long-term reward value of taking specific action in a specific state. According to the Q table, the Q learning algorithm can tell the Q agent which action to choose in a specific situation to get the largest expected reward.
In a certain iteration, the agent of the Q-learning algorithm is in the state
When the problem scale is larger, Q-table will be inefficient. Therefore, Deep Q-learning had been developed to use a neural network to approximate the Q-value function. The state is given as the input and the Q-value of all possible actions is generated as the output.
Dijkstra's algorithm is a greedy algorithm that can find the lengths of shortest path in a graph.
The input is the graph and the source node, and the distance of every other node is marked as infinity.
Below is the pseudocode:
dist[v]is the length from source node to nodevQis a queue that stores nodes that will be processed later. This is usually implemented by binary heap or fibonacci heap in order to get minimum node.
function Dijkstra(Graph, source):
for each vertex v in Graph.Vertices:
dist[v] ← INFINITY
prev[v] ← UNDEFINED
add v to Q
dist[source] ← 0
while Q is not empty:
u ← vertex in Q with min dist[u]
remove u from Q
for each neighbor v of u still in Q:
alt ← dist[u] + Graph.Edges(u, v)
if alt < dist[v]:
dist[v] ← alt
prev[v] ← u
return dist[], prev[]
This algorithm always choose the node with minimum distance from Q, and update the distance of its neighbor nodes.
Other than dist, the code above also return another array prev.
prev[v] will be the previous node of v on the shortest path from source to v.
-
Objective:Minimize the waiting time of every passenger.
-
Setting up a map existing multiple taxis and passengers, which is called a grid map.
-
The map size is 100 x 100, and the coordinates of the lower left and upper right position is (0, 0) and (99, 99) respectively.
-
The number of passengers is 40, this number is fixed in every episode.
-
In each episode, reset all passengers' positions and destinations.
-
The number of taxi is 20, this number is fixed in every episode.
-
In the map, a random cost is set between every pair of adjacent nodes, the random cost is the number of steps required for the taxi to go to the next node.
""" Set the weight of edges in the grid map with random value """ def init_map_cost(self): for row in range(self.size[0]): for col in range(self.size[1]): p = (row, col) p_down = (row + 1, col) if self.is_valid(p_down): self.map_cost[(p_down, p)] = self.map_cost[(p, p_down)] = random.randint(1, 9) p_right = (row, col + 1) if self.is_valid(p_right): self.map_cost[(p_right, p)] = self.map_cost[(p, p_right)] = random.randint(1, 9)
-
-
We measure the duration time in discret time.
-
One duration is one step forward for all taxis on the map that have paired passengers.
-
An episode(iteration) is completed when all passengers have been sent to their respective destinations.
-
-
Every passenger is represented as two points, pick-up position and destination.
-
The capacity of taxi is 2, which means that the number of passengers on each taxi shouldn’t exceed 2 at any moment.
-
There are no group passengers, which means that every passenger is individual.
-
The rule of dropping by:
-
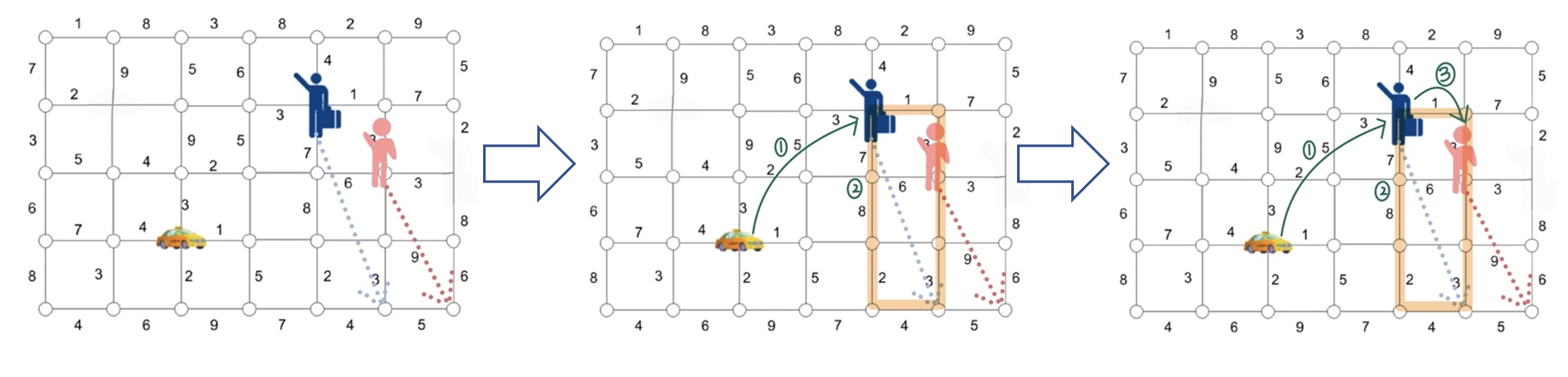
There are one taxi and two passengers(the blue one and the pink one) on the map in this example.
-
Both passengers own their recent position and destination and are assigned to this taxi.
1. The taxi comes to pick the blue passenger up. 2. When the taxi moved to the position of the blue passenger, the system will judge whether there is other passenger on the way(the place surrounded by the orange frame). 3. If there is other passenger(the pink one), the taxi will pick up the second passenger first, then go to the destination of the first passenger(the blue one). 4. Otherwise, go directly to the destination of the passenger.
-
Every passenger will be taken by the nearest taxi in L1 distance.
- All Passengers
-
$(c_x, c_y)$ , positions of all taxis. -
$(p_x, p_y)$ , pick-up point of all passengers. -
$(d_x, d_y)$ , destination of all passengers.
- An 1-D array
$a$ that represent the index of the taxi to take the passenger.
For example:
Assume the number of passengers is 5, [0, 3, 1, 2, 3] may be one possible action.
Below is the table that explains what [0, 3, 1, 2, 3] means.
| Passenger index | Assigned Taxi index |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
- Waiting time of every passenger.
The position of taxis at the end of this episode will effect the duration of next episode.
Thus we only set the passengers' positions and destinations with random numbers.
The randomly generated state will be the
class Environment:
def __init__(self, grid_map):
self.grid_map = grid_map
"""
Reset the passengers on the grid map
"""
def reset(self):
self.grid_map.passengers = []
self.grid_map.add_passengers(self.grid_map.num_passengers)Because initially the agent doesn't know how to determine the action, this method allows the agent to learn different ways to determine action by randomly choosing it.
As the experiment progresses, the value of
By using this method, the agent will tend to randomly choose action at beginning, and will tend to determine action by what it learned at the end.
-
Reason to use duration : All taxis go forward with a step representing a duration, and if all the passengers arrive at their destinations, an episode is completed. A shorter episode time means better performance, because the wating time of all passengers will be less.
-
The loss is calculated by Huber loss function mentioned in the reference paper and Pytorch tutorial, because this is more robust to outliers when the estimates of waiting time are very noisy. The formula of Huber loss is shown below:
-
$\delta$ is the difference between$Q^{\text{new}}(s, a)$ and$Q^{\text{old}}(s, a)$
-
| Name | Value |
|---|---|
| 0.1 | |
| 0.8 | |
| 0.9 | |
| 0.05 | |
| replay memory capacity | 10000 |
| batch size |
128 |
In this experiment, we use another algorithm to find the path instead of using Dijkstra's Algorithm.
Because every node is connected to its adjacent nodes, the algorithm below is enough to find the path.
"""
Find the shortest path from `start_point` to `end_point`.
Notes that the length of path here is measured by Manhattan distance between points
instead of the weight of edges on the path.
Returned path: (start_point, end_point]
"""
def plan_path_two_points(self, start_point, end_point):
x, y = start_point
path = []
step = 1 if x <= end_point[0] else -1
while x != end_point[0]:
x += step
path.append((x, y))
step = 1 if y <= end_point[1] else -1
while y != end_point[1]:
y += step
path.append((x, y))
return path| 500 iterations | 1000 iterations | 2000 iterations | |
|---|---|---|---|
| DQN | 3153.31 | 3128.533 | 3274.5275 |
| Greedy | 3652.652 | 3770.124 | 3768.404 |
In the real world, not every road is bidirectional.
If there is a road construction, the road is even closed to traffic.
Thus we want to drop (cut) some edges to make the environment more closed to real world.
After dropping some edges, not every node is connected to its adjacent nodes.
Therefore we need to use BFS or similar algorithm to find the path, and here we use Dijkstra's Algorithm.
Here is the duration comparison of DQN and Greedy algorithm.
| drop 1000 edges | drop 2000 edges | |
|---|---|---|
| DQN | 2060.556 | 2138.1075 |
| Greedy | 2333.24 | 2388.7645 |
In carpooling problem, we consider the opposite situation of addressing problem of scheduling a fleet of taxis, focusing on providing user(passenger) a option to choose a taxi which can let user has the shortest waiting time and try to solve the problem using the reinforcement learning method.
From the result, we can find that DQN has the better performance rather than Greedy algorithm no matter in experiment1 or experiment2.
Future directions for extending this work include considering the relationship of individual passenger, which means if two(three or four etc.) of passengers are family(friendes etc.) then the taxi should pick up all of them whether on the way or not and also giving a restriction to taxi that if it is out of energy then it can not move anymore.
Moreover, as for passenger, except the waiting time, the expense of taking a taxi is very likely to be a concern point(as long as waiting for a while, the cost could be decreased). Thus, adding cost term to the objective function of this study or reformulating the objective function by considering the combination of the waiting time and the cost is also a good choice.
- Efficient Ridesharing Dispatch Using Multi-Agent Reinforcement Learning
- https://www.freecodecamp.org/news/dijkstras-algorithm-explained-with-a-pseudocode-example/
- https://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html