二叉排序树的操作

[FocusOn1]

一．实验目的

（1）掌握二叉排序树的特点；
（2）掌握二叉排序树的插入操作；
（3）掌握二叉排序树的建立算法，明白二叉排序树的建立实际上就是一个插入结点的过程。
（4）掌握二叉排序树的查找操作；
（5）掌握二叉排序树的删除操作。

二．实验内容

编程实现：
（1）输入一数列，建立二叉排序树；
（2）对所建立的二叉排序树进行查找操作，找到了就显示，找不到就插入；
（3）对所建立的二叉排序树进行删除操作。

三．源程序及主要算法说明

//二叉排序树
//其中有插入、删除、查找操作
#include<stdio.h>
#include<stdlib.h>
#define FALSE 0
#define TURE 1
#define MAXSIZE 10
typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
//查找
//f指向T的双亲，初始时为NULL
//这里用f，*p，是问了存储查找时遍历的最后一个元素，在插入时用
int SearchBST(BiTree T,int key,BiTree f,BiTree *p)
{
    if( !T   )
    {
        *p=f;
        return FALSE; 
    }
    else if( key==T->data)
    {
        *p=T;
        return TURE;
    }
    else if(key<T->data)
        return SearchBST( T->lchild,key,T,p);
    else
        return SearchBST( T->rchild,key,T,p);
}
//插入
//如果插不到元素，获取查找时遍历的最后一个元素
//与其比较，大则是其右子树，反之、、
void InsertBST(BiTree *T,int key)
{
    BiTree p,s;
    if(  !SearchBST(*T,key,NULL,&p)  )      //若树中没有相同元素，继续
    {
        s=(BiTree)malloc(sizeof(BiTNode));
        s->data=key               ;
        s->lchild=s->rchild=NULL;       //设置新元素s
        if(!p)      //若树为空，将s设为根节点
            *T=s;
        else if( key<p->data )        //否则。。
            p->lchild=s;
        else
            p->rchild=s;
    }
    else
        printf("抱歉，树中已有该元素。 \n");
}
//DeleteBST用到的子函数
//删除节点无左子树，则将其右子树补到现在位置，反之亦然
//若左右字树都有，则找其左子树，然后右到底，即中序遍历时，删除节点的上一个元素——前驱
//以前驱作为新节点
void Delete(BiTree *p)
{
    BiTree q,s;
    if( (*p)->rchild==NULL )      //无右，以左子树替换
    {
        q=*p;
        *p=(*p)->lchild;
        free(q);
    }
    else if(    (*p)->lchild==NULL     )     //无左    
    {
        q=*p;
        *p=(*p)->rchild;
        free(q);
    }
    else
    {
        q=*p;
        while(s->rchild)    //右到底
        {
            q=s;
            s=s->rchild;
        }
        (*p)->data=s->data;     //前驱替换删除节点
        free(s);
    }
}
//删除
void DeleteBST(BiTree *T,int key)
{
    BiTree p;
    if(SearchBST(*T,key,NULL,&p))       //找与key相等的元素
    {
        if(key==(*T)->data)
            Delete(T);
        else if(key<(*T)->data)
           DeleteBST(&(*T)->lchild,key);
        else
           DeleteBST(&(*T)->rchild,key);
    }
    else
        printf("抱歉，当前二叉树中没有你要删除的元素。 \n");
}
//中序输出
void InOrder(BiTree T)
{
    if(T)
    {
        InOrder(T->lchild);
        printf("%d ",T->data);
        InOrder(T->rchild);
    }
    else
        return;
}

int main()
{
    int i, num,index, k, n, temp;
    BiTree T=NULL;
    int a[10];         	/* 定义1个数组a，它有10个整型元素*/
    printf("输入 n: ");                /* 提示输入n */
    scanf("%d", &n);
    printf("输入 %d 个数: ", n);   /* 提示输入n 个数 */
    for(i = 0; i < n; i++)				/* 将输入数依次赋给数组a的n个元素a[0]～a[n-1] */   
        scanf("%d", &a[i]);
    /* 对n个数排序 */
    for(k = 0; k < n-1; k++){
        index = k;						/* index存放最小值所在的下标 */
        for(i = k + 1; i < n; i++)		/* 寻找最小值所在下标 */
            if(a[i] < a[index])  index = i;    
        temp = a[index];				/* 最小元素与下标为k的元素交换 */
        a[index] = a[k];
        a[k] = temp;
    }
//    printf("After sorted: ", n);		/* 输出n个数组元素的值 */
//    for(i = 0; i < n; i++)       
//        printf("%d ", a[i]);
//    printf("\n");
// 	
    for(i=0;i<n;i++)
    {
       InsertBST(&T,a[i]);
    }
    printf("当前的二叉树为：");
    InOrder(T);
    printf("\n");
    printf("请输入你要插入的元素：");
    scanf("%d",&num);
    InsertBST(&T,num);
    printf("当前的二叉树为：");
    InOrder(T);
    printf("\n");
    printf("请输入你要删除的元素：");
    scanf("%d",&num);
    DeleteBST(&T,num);
    printf("当前的二叉树为：");
    InOrder(T);
    printf("\n");
}

四、主要问题和解决方案

【主要问题】在删除代码这里出错了。有些可以删除有些不能删除？

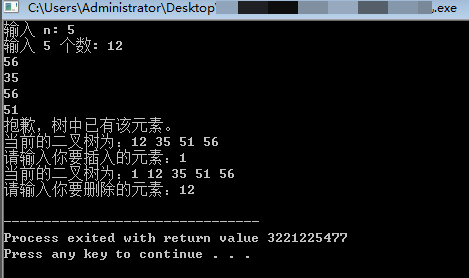
五、测试数据及结果