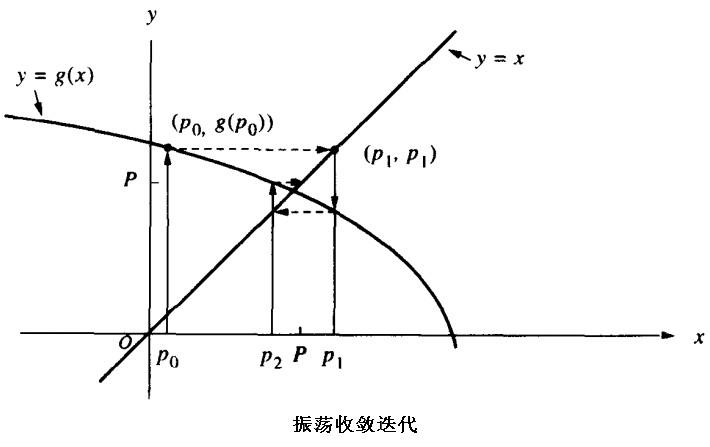
-
不动点迭代：
一个函数 f 的不动点就是满足$f(x)=x$的点，这个不动点就是$f(x)$和$y=x$之间的交点，可以用迭代的方法来求解：$x_{n+1}=f(x_n)$重复这个操作直到$x_n$收敛
-
牛顿迭代法： $$ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} $$
-
泰勒展开式
泰勒级数就是在某个点附近用多项式去逼近其他函数。基本形式为： $$ f(x)=\sum_{k=0}^N\frac{f^k(x_0)}{k!}(x-x_0)^k $$
-
样条函数插值：
拉格朗日多项式表示： $$ y=y_0\frac{x-x_1}{x_0-x_1}+y_1\frac{x-x_0}{x_1-x_0} $$ 构建多项式，使得它穿过目标函数上的样本点，样本点见用多项式来拟合。
-
数值微分
要求某一点的导数，可以通过差分的方法求解：
- 前向差分：$f'(x)=\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}$，误差为$O(h)$
- 后向差分：$f'(x)=\frac{f(x_{i})-f(x_i-1)}{x_{i}-x_{i-1}}$，误差为$O(h)$
- 中心差分：$f'(x)=\frac{f(x_{i+1})-f(x_{i-1})}{x_{i+1}-x_{i-1}}$，误差为$O(h^2)$
