Digital Communication Assignments

Table of Contents

• 📙 Overview
• 📝 Assignments
  • ☝️ Assignment 1
  • ✌️ Assignment 2
  • 👌 Assignment 3
• ✨ Contributors
• 🔒 License

---

Overview

• Solution of assignment in course Digital communications ELC325B
• This project has solutions for 3 assignments
• Assignment 1
• Assignment 2
• Assignment 3
• Built using Matlab

---

Assignments

Assignment 1

• This assignment is mainly talking about using uniform quantizer and see the affect of this quantizer on both uniform signal and non-uniform ones with small modification on the quantizer
• calculating the signal to noise ratio for each to compare results when different number of bits are used to transmit the signal which means a more or less resolution on transmitting
• for the non-uniform signal we used smaller quantization steps for smaller signal amplitudes this achieved through compressing the signal using the μ-Law Companding Technique then applying uniform quantizer which is equivalent to non-uniform quantization
• View Assignment 1

Title	Image	Description
Uniform Quantizer		Function is responsible to quantize and encode the transmitted signal to a specific number of levels specified by the number of bits it takes so the block outputs the zero-based index of the associated region
Uniform De Quantizer		which was mainly responsible to decode the quantized signal and get the range back to the originally transmitted signal using previously calculated delta and x_min values
Quantize Dequantize Ramp Signal		Midrise Figure The figure shows a ramp function (dashed) which values ranges from -6 to 6 and the output of the quantizer and dequantizer for this signal where we used the mid-rise staircase for transmitting and using number of bits = 3 which leads to have 8 levels of values. the origin lies in the middle of a raising part of the stair-case like graph. Midtread Figure This figure shows the same ramp function (dashed) but when we used the mid-tread staircase for transmitting the signal, as shown the origin lies in the middle of a tread of the stair-case like graph.
Uniform Quantizer and De Quantizer on uniform random Signal		The signal-to-noise ratio (SNR) is one of the performance measures used to describe communication systems. In this particular figure we did generate a uniform random function and tried to transmit it at different number of levels to see the affect of quantizer and dequantizer on it.
Uniform Quantizer and De Quantizer on non-uniform random Signa		For this figure we generated a non-uniform random function and tried the uniform quantizer on it and we discovered that for small number of bits we transmit at. The SNR value was less than expected and theoretically proved in equations as it is a uniform quantizer applied on a non-uniform signal, in the other hand at higher number of bits we can hardly see a difference.
Using a non-uniform 𝝁 law quantizer		For this part we used non-uniform μ-Law quantizer for different μ-val using zero value for the μ means uniform quantizing the signal the blocks output exactly the same graph as last mentioned one and for different μ-values we could obviously see the difference between theoretically calculated SNR and experimentally calculated one

Assignment 2

View Assignment 2

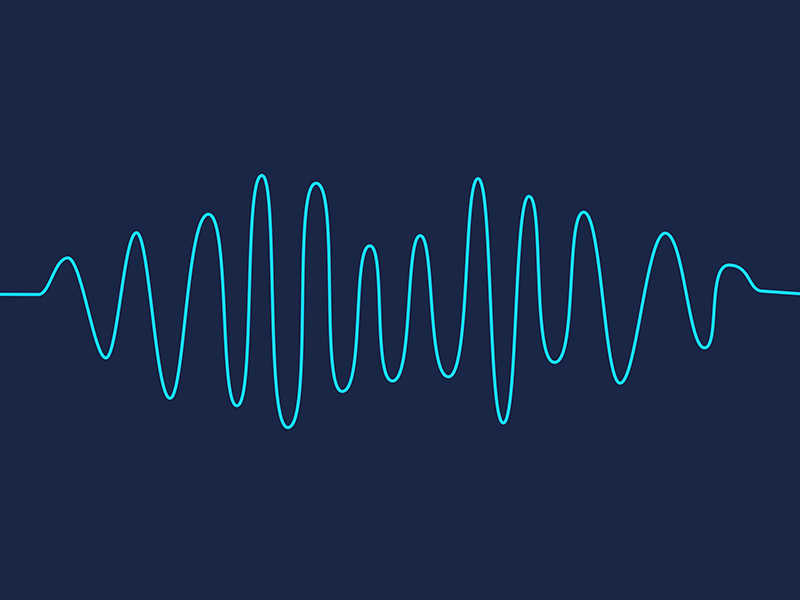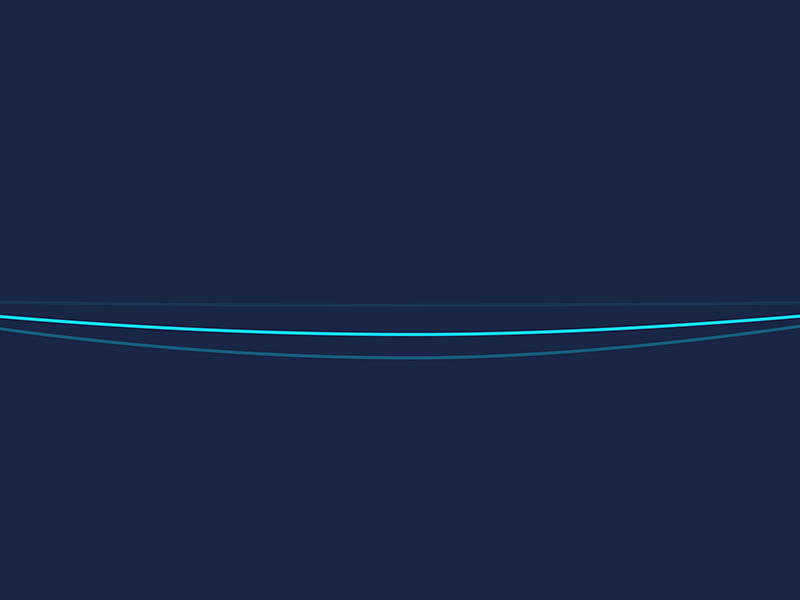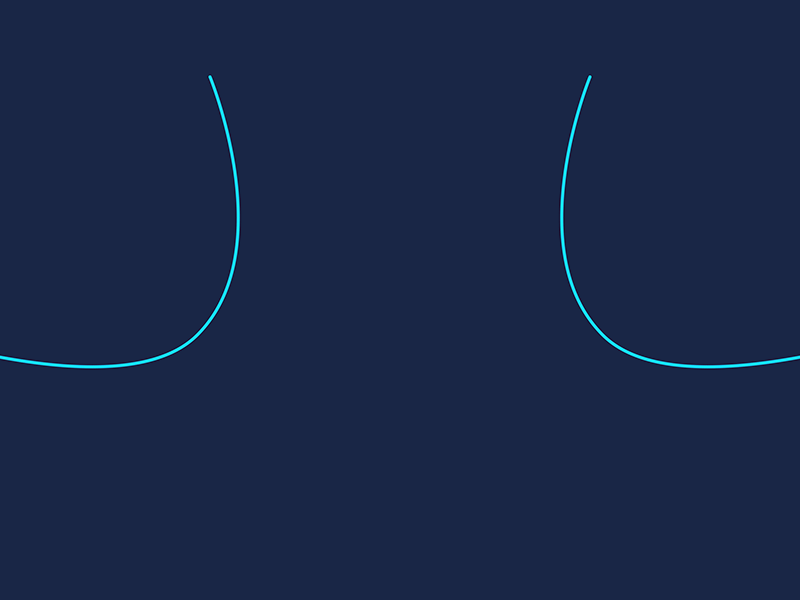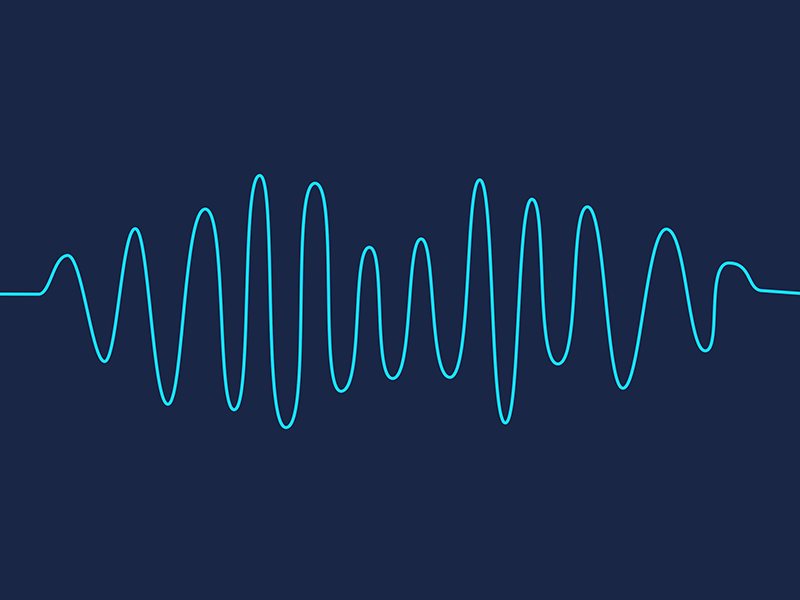
Plot the output of the receive filter for the three mentioned cases For input: 0011000011

Description	Image
On the same figure, plot the theoretical and simulated Bit Error Rate (BER) Vs E/𝑵𝒐 (where E is the average symbol energy) for the three mentioned cases. Take E/No to be in the range -10 dB: 20:dB. (Use a semilogy plot)

Assignment 3

Gram-Schmidt orthogonalization is a mathematical procedure that takes a set of linearly independent vectors and constructs an orthogonal or orthonormal set of vectors that span the same subspace. It is commonly used in linear algebra and signal processing.

View Assignment 3

Description	Image
Φ1 VS time after using the GM_Bases function
Φ2 VS time after using the GM_Bases function
Signal Space representation of signals s1,s2
Signal Space representation of signals s1,s2 with E/σ¬2 =10dB
Signal Space representation of signals s1,s2 with E/σ¬2 =0dB
Signal Space representation of signals s1,s2 with E/σ¬2 =-5dB

---

Contributors

Nour Ziad Almulhem

Eslam Ashraf

🔒 License

This software is licensed under MIT License, See License for more information ©Nour.