You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
{{ message }}
This repository has been archived by the owner on Mar 1, 2024. It is now read-only.
function _calculateCheckpointReward(uint256 blockInterval, uint256 signedStakePower, uint256 currentTotalStake) internal returns (uint256) {
// ......
if (blockInterval > targetBlockInterval) {
// count how many full intervals
uint256 _rewardDecreasePerCheckpoint = rewardDecreasePerCheckpoint;
// calculate reward for full intervals
reward = ckpReward.mul(fullIntervals).sub(ckpReward.mul(((fullIntervals - 1) * fullIntervals / 2).mul(_rewardDecreasePerCheckpoint)).div(CHK_REWARD_PRECISION));
// adjust block interval, in case last interval is not full
blockInterval = blockInterval.sub(fullIntervals.mul(targetBlockInterval));
// adjust checkpoint reward by the amount it suppose to decrease
ckpReward = ckpReward.sub(ckpReward.mul(fullIntervals).mul(_rewardDecreasePerCheckpoint).div(CHK_REWARD_PRECISION));
}
// give proportionally less for the rest
reward = reward.add(blockInterval.mul(ckpReward).div(targetBlockInterval));
reward = reward.mul(signedStakePower).div(currentTotalStake);
return reward;
Let's give these variables a simple name as follow:
x: input blockInterval
p: input signedStakePower
q: input currentTotalStake
t: checkPointBlockInterval or targetBlockInterval
d: rewardDecreasePerCheckpoint
m: maxRewardedCheckpoints
n: fullIntervals
e: blockInterval.sub(fullIntervals.mul(targetBlockInterval))
r: ckpReward
y: returning reward
They satisfy the following relationships:
x = n * t + e, n <= m
Since n max is m, the number of remaining blocks in x is e. Thus when x has exceeded m * t, then n = m, e increases with x. Thus, the terms in the polynomial related to n become constants, and the final result y increases as e increases. Does this incite proposers to wait for more blocks to submit?
The text was updated successfully, but these errors were encountered:
Sign up for freeto subscribe to this conversation on GitHub.
Already have an account?
Sign in.
Let's give these variables a simple name as follow:
x: input blockInterval
p: input signedStakePower
q: input currentTotalStake
t: checkPointBlockInterval or targetBlockInterval
d: rewardDecreasePerCheckpoint
m: maxRewardedCheckpoints
n: fullIntervals
e: blockInterval.sub(fullIntervals.mul(targetBlockInterval))
r: ckpReward
y: returning reward
They satisfy the following relationships:
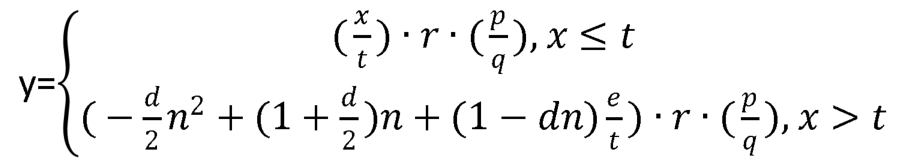
x = n * t + e, n <= m
Since n max is m, the number of remaining blocks in x is e. Thus when x has exceeded m * t, then n = m, e increases with x. Thus, the terms in the polynomial related to n become constants, and the final result y increases as e increases. Does this incite proposers to wait for more blocks to submit?
The text was updated successfully, but these errors were encountered: