欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
这篇可以说是全网把组合问题如何去重,讲的最清晰的了!
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。 解集不能包含重复的组合。
示例 1: 输入: candidates = [10,1,2,7,6,1,5], target = 8, 所求解集为: [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ]
示例 2: 输入: candidates = [2,5,2,1,2], target = 5, 所求解集为: [ [1,2,2], [5] ]
如果对回溯算法基础还不了解的话,我还特意录制了一期视频:带你学透回溯算法(理论篇) 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
这道题目和39.组合总和如下区别:
- 本题candidates 中的每个数字在每个组合中只能使用一次。
- 本题数组candidates的元素是有重复的,而39.组合总和是无重复元素的数组candidates
最后本题和39.组合总和要求一样,解集不能包含重复的组合。
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。
一些同学可能想了:我把所有组合求出来,再用set或者map去重,这么做很容易超时!
所以要在搜索的过程中就去掉重复组合。
很多同学在去重的问题上想不明白,其实很多题解也没有讲清楚,反正代码是能过的,感觉是那么回事,稀里糊涂的先把题目过了。
这个去重为什么很难理解呢,所谓去重,其实就是使用过的元素不能重复选取。 这么一说好像很简单!
都知道组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。
那么问题来了,我们是要同一树层上使用过,还是同一树枝上使用过呢?
回看一下题目,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
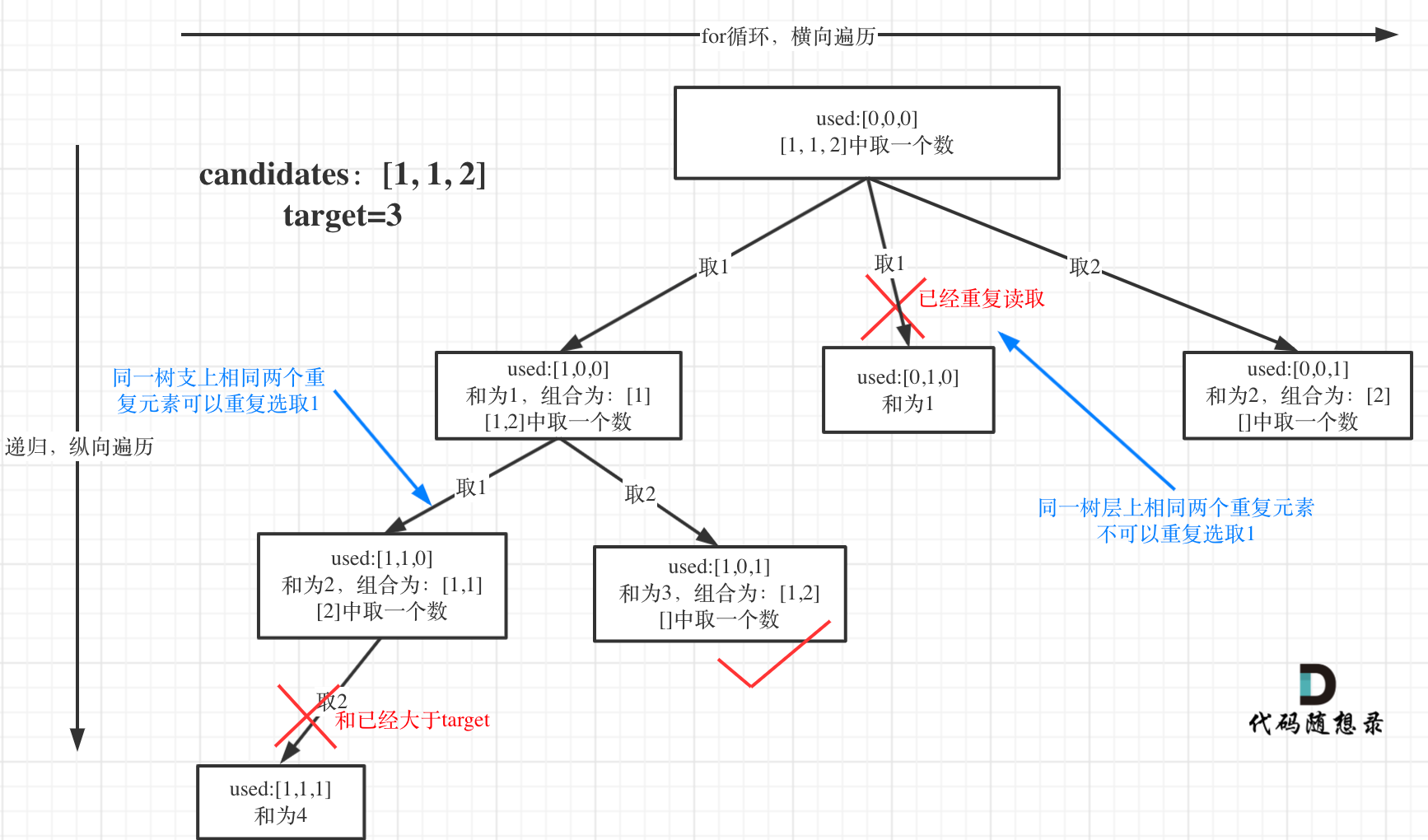
为了理解去重我们来举一个例子,candidates = [1, 1, 2], target = 3,(方便起见candidates已经排序了)
强调一下,树层去重的话,需要对数组排序!
选择过程树形结构如图所示:
可以看到图中,每个节点相对于 39.组合总和我多加了used数组,这个used数组下面会重点介绍。
- 递归函数参数
与39.组合总和套路相同,此题还需要加一个bool型数组used,用来记录同一树枝上的元素是否使用过。
这个集合去重的重任就是used来完成的。
代码如下:
vector<vector<int>> result; // 存放组合集合
vector<int> path; // 符合条件的组合
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {- 递归终止条件
与39.组合总和相同,终止条件为 sum > target 和 sum == target。
代码如下:
if (sum > target) { // 这个条件其实可以省略
return;
}
if (sum == target) {
result.push_back(path);
return;
}sum > target 这个条件其实可以省略,因为和在递归单层遍历的时候,会有剪枝的操作,下面会介绍到。
- 单层搜索的逻辑
这里与39.组合总和最大的不同就是要去重了。
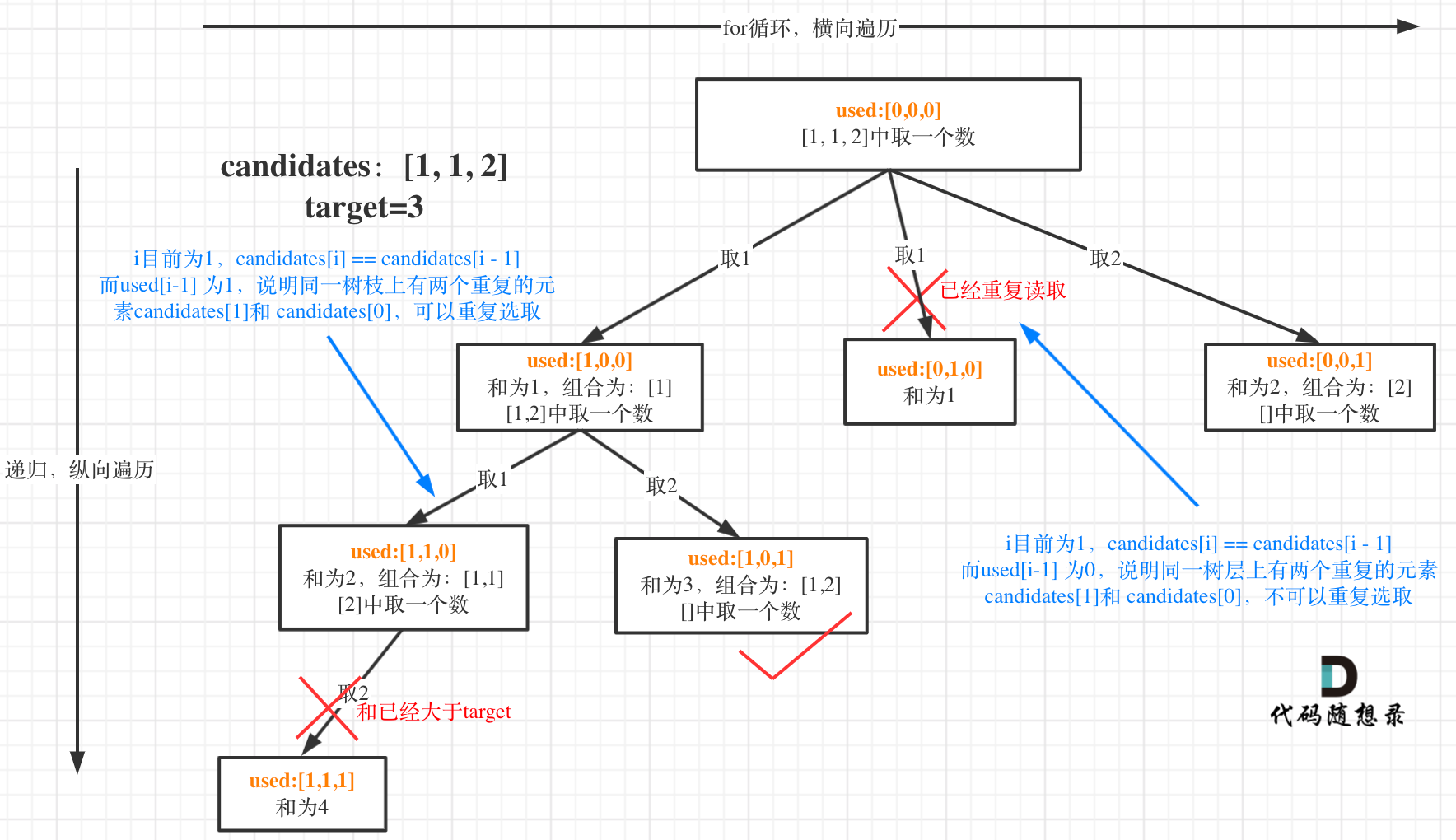
前面我们提到:要去重的是“同一树层上的使用过”,如果判断同一树层上元素(相同的元素)是否使用过了呢。
如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false,就说明:前一个树枝,使用了candidates[i - 1],也就是说同一树层使用过candidates[i - 1]。
此时for循环里就应该做continue的操作。
这块比较抽象,如图:
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树支candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!
那么单层搜索的逻辑代码如下:
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true;
backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1:这里是i+1,每个数字在每个组合中只能使用一次
used[i] = false;
sum -= candidates[i];
path.pop_back();
}注意sum + candidates[i] <= target为剪枝操作,在39.组合总和有讲解过!
回溯三部曲分析完了,整体C++代码如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true;
backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
used[i] = false;
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false);
path.clear();
result.clear();
// 首先把给candidates排序,让其相同的元素都挨在一起。
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0, used);
return result;
}
};
这里直接用startIndex来去重也是可以的, 就不用used数组了。
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
// 要对同一树层使用过的元素进行跳过
if (i > startIndex && candidates[i] == candidates[i - 1]) {
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i + 1); // 和39.组合总和的区别1,这里是i+1,每个数字在每个组合中只能使用一次
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
path.clear();
result.clear();
// 首先把给candidates排序,让其相同的元素都挨在一起。
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0);
return result;
}
};
本题同样是求组合总和,但就是因为其数组candidates有重复元素,而要求不能有重复的组合,所以相对于39.组合总和难度提升了不少。
关键是去重的逻辑,代码很简单,网上一搜一大把,但几乎没有能把这块代码含义讲明白的,基本都是给出代码,然后说这就是去重了,究竟怎么个去重法也是模棱两可。
所以Carl有必要把去重的这块彻彻底底的给大家讲清楚,就连“树层去重”和“树枝去重”都是我自创的词汇,希望对大家理解有帮助!
class Solution {
List<List<Integer>> lists = new ArrayList<>();
Deque<Integer> deque = new LinkedList<>();
int sum = 0;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
//为了将重复的数字都放到一起,所以先进行排序
Arrays.sort(candidates);
//加标志数组,用来辅助判断同层节点是否已经遍历
boolean[] flag = new boolean[candidates.length];
backTracking(candidates, target, 0, flag);
return lists;
}
public void backTracking(int[] arr, int target, int index, boolean[] flag) {
if (sum == target) {
lists.add(new ArrayList(deque));
return;
}
for (int i = index; i < arr.length && arr[i] + sum <= target; i++) {
//出现重复节点,同层的第一个节点已经被访问过,所以直接跳过
if (i > 0 && arr[i] == arr[i - 1] && !flag[i - 1]) {
continue;
}
flag[i] = true;
sum += arr[i];
deque.push(arr[i]);
//每个节点仅能选择一次,所以从下一位开始
backTracking(arr, target, i + 1, flag);
int temp = deque.pop();
flag[i] = false;
sum -= temp;
}
}
}class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
path = []
def backtrack(candidates,target,sum,startIndex):
if sum == target: res.append(path[:])
for i in range(startIndex,len(candidates)): #要对同一树层使用过的元素进行跳过
if sum + candidates[i] > target: return
if i > startIndex and candidates[i] == candidates[i-1]: continue #直接用startIndex来去重,要对同一树层使用过的元素进行跳过
sum += candidates[i]
path.append(candidates[i])
backtrack(candidates,target,sum,i+1) #i+1:每个数字在每个组合中只能使用一次
sum -= candidates[i] #回溯
path.pop() #回溯
candidates = sorted(candidates) #首先把给candidates排序,让其相同的元素都挨在一起。
backtrack(candidates,target,0,0)
return res主要在于如何在回溯中去重
func combinationSum2(candidates []int, target int) [][]int {
var trcak []int
var res [][]int
var history map[int]bool
history=make(map[int]bool)
sort.Ints(candidates)
backtracking(0,0,target,candidates,trcak,&res,history)
return res
}
func backtracking(startIndex,sum,target int,candidates,trcak []int,res *[][]int,history map[int]bool){
//终止条件
if sum==target{
tmp:=make([]int,len(trcak))
copy(tmp,trcak)//拷贝
*res=append(*res,tmp)//放入结果集
return
}
if sum>target{return}
//回溯
// used[i - 1] == true,说明同一树支candidates[i - 1]使用过
// used[i - 1] == false,说明同一树层candidates[i - 1]使用过
for i:=startIndex;i<len(candidates);i++{
if i>0&&candidates[i]==candidates[i-1]&&history[i-1]==false{
continue
}
//更新路径集合和sum
trcak=append(trcak,candidates[i])
sum+=candidates[i]
history[i]=true
//递归
backtracking(i+1,sum,target,candidates,trcak,res,history)
//回溯
trcak=trcak[:len(trcak)-1]
sum-=candidates[i]
history[i]=false
}
}/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
var combinationSum2 = function(candidates, target) {
const res = []; path = [], len = candidates.length;
candidates.sort();
backtracking(0, 0);
return res;
function backtracking(sum, i) {
if (sum > target) return;
if (sum === target) {
res.push(Array.from(path));
return;
}
let f = -1;
for(let j = i; j < len; j++) {
const n = candidates[j];
if(n > target - sum || n === f) continue;
path.push(n);
sum += n;
f = n;
backtracking(sum, j + 1);
path.pop();
sum -= n;
}
}
};int* path;
int pathTop;
int** ans;
int ansTop;
//记录ans中每一个一维数组的大小
int* length;
int cmp(const void* a1, const void* a2) {
return *((int*)a1) - *((int*)a2);
}
void backTracking(int* candidates, int candidatesSize, int target, int sum, int startIndex) {
if(sum >= target) {
//若sum等于target,复制当前path进入
if(sum == target) {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int j;
for(j = 0; j < pathTop; j++) {
tempPath[j] = path[j];
}
length[ansTop] = pathTop;
ans[ansTop++] = tempPath;
}
return ;
}
int i;
for(i = startIndex; i < candidatesSize; i++) {
//对同一层树中使用过的元素跳过
if(i > startIndex && candidates[i] == candidates[i-1])
continue;
path[pathTop++] = candidates[i];
sum += candidates[i];
backTracking(candidates, candidatesSize, target, sum, i + 1);
//回溯
sum -= candidates[i];
pathTop--;
}
}
int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
path = (int*)malloc(sizeof(int) * 50);
ans = (int**)malloc(sizeof(int*) * 100);
length = (int*)malloc(sizeof(int) * 100);
pathTop = ansTop = 0;
//快速排序candidates,让相同元素挨到一起
qsort(candidates, candidatesSize, sizeof(int), cmp);
backTracking(candidates, candidatesSize, target, 0, 0);
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}