Papers:
《LOAM_Lidar Odometry and Mapping in Real-time》
《Low-drift and real-time lidar odometry and mapping》
《On Degeneracy of Optimization-based State Estimation Problems》
源码:
https://github.com/daobilige-su/loam_velodyne 可以参考这个版本
LOAM源码主要由四个节点构成,分别完成特征点提取,高频低精度odom, 低频高精度odom, 双频odom融合的功能,每个节点以rosnode的形式存在, 也就是说是独立的进程,进程间通过rostopic传递点云, odom等数据。实际上, 四个节点的执行顺序完全是串行的,很容易改成单进程的版本。
以下为各节点的简述:
根据VLP16的激光扫描模型, 对单帧点云(paper中称为一个Sweep)进行分线束(分为16束), 每束称为一个Scan, 并记录每个点所属线束和每个点在此帧电云内的相对扫描时间(相对于本帧第一个点)。
针对单个Scan提取特征点, 而相对时间会在laserOdometry中用于运动补偿.所有Scan的特征点,拼到两个点云中(因为是corner和surface两种特征点,所以是两个点云).至此,每帧点云,输出两帧对应的特征点云, 给下一个节点laserOdometry。
实现运动补偿和帧间配准.每帧激光都会参与(所以帧率同VLP16的扫描帧率,10hz).通过对每一帧激光的配准,可以得到一个精度较差的ODOM,帧与帧配准的初始POSE可以由IMU得到,或者在没有IMU的时候由匀速运动模型(简单的说就是假设这一帧运动量与上一帧一致)得到。
本节点输出的ODOM频率为10hz.此ODOM的作用:
(a) 在laserMapping中用于位姿的预测。
(b) 在transformMaintenance中为laserMapping输出的低频ODOM提供插值,以获得高频(10HZ)的ODOM.
在实际应用中,帧间匹配实现的ODOM,可以由IMU, 视觉里程计,底盘编码器等替代.而运动补偿在高速场景是不可或缺的.
本节点使用实现了一个较为完整的SLAM过程,也就是同时建图和定位.主要工作:
(a)通过将多帧的激光特征点云基于POSE拼接,形成特征点云地图.前面有提到特征包含corner和surface两种,那么这里就是建立了两种特征点云地图.
(b)将新入的帧与地图作配准,得到更精准的POSE.我们又将基于这个POSE执行a过程进行建图。
由于单帧与地图配准计算量较大,本节点没有将所有帧与地图进行配准,而是间隔几帧,比如每5帧配准一次(那么频率就是2hz).如果你的应用场景运算性能完全够, 你可以一帧一匹配.如果这样, transformMaintenance这个节点就没有存在的意义了.
如果你能将本节点生成的特征地图存下来, 那么就可以将这些地图作为离线地图。我们可以在在线场景中, 把这个地图输入给laserMapping节点,实现定位的功能.
当然这个地图功能还不够完善,比如没有回环检测,这时候可以参考LeGO-LOAM,此文运用iSAM和icp实现了回环检测和全局优化的建图功能,此处不再赘述。
laserOdometry和laserMapping中都涉及到点云配准问题.
点云的配准问题一般有一个source和一个target,配准的目的是旋转和平移source点云使得source点云与target点云尽量重叠.
在laserOdometry中配准的source是新一帧的点云,target是前一帧的点云.
在laserMapping中配准的source是新一帧的点云,target是前面的点云拼接成的地图.
当然,我们这里说的点云指的是特征点云, 分为corner和surface两种,corner对应corner map, surface对应surface map.
优化流程:
通过ODOM预测得到初始位姿,source中的corner在target的corner中寻找对应直线, source中的surface在target的surface中寻找对应平面,
通过点-线和点-面关联共同构建约束, 以点线距离和点面距离作为loss, 基于非线性最小二乘的方法进行优化.求解得出最优pose.
本处只为简述laserOdometry和laserMapping中的共性,配准优化的具体细节后面会详述.
使用laserOdometry输出的odom(高频率)对laserMapping输出的odom(低频率)进行插值
在运动的汽车上,比如说速度为10m/s,直行, 无旋转运动.激光扫描频率为10hz, 也就是一帧0.1秒,雷达在这0.1秒内实现了约360度的旋转.那么0°和360°的激光点, 分别是在时刻0秒和时刻0.1秒扫描的.而第0秒和0.1秒,载具移动了10米/秒*0.1秒=1米.
激光返回的点云中的点, 描述的是激光雷达坐标系下的坐标,假设0秒时,激光雷达扫描得到载具正前方一百米处的一个点A, 记下其在雷达坐标系下的坐标为(100, 0, 0), 扫描完了一圈, 激光雷达输出一帧点云, 时间戳为0.1秒.也就是说, 激光雷达在0.1秒时, 输出点A的坐标为(100,0,0),而实际, 在0.1秒时, 汽车已经前进了1米, 点A在0.1秒这个时刻激光坐标系的真实坐标应该是(99, 0, 0).
若我们知道每个点扫描的具体时间, 比如知道点B是在0.05秒时被扫描到的,结合这0.05秒载具的相对运动, 我们可以对点B的坐标位置进行修复。包含旋转的情况亦然.
在LOAM中,laserOdometry节点在配准前基于IMU或者匀速运动模型实现了运动补偿。
在没有外部观测的情况下,一般使用航位推算的方法对位姿进行预测,比如我们已知t时刻的pose为, 我们可以基于其他的odom信息(比如底盘编码器,视觉里程计,IMU)进行航位推算.以底盘为例,假如t, t+1时刻底盘odom的对应的pose为,, 我们可以得到载具在t->t+1时刻的相对pose变换T:
可得:
其中, 指的是Odom 在t+1时刻位姿向t时刻位姿的相对变换。
由于噪音的引入, odom是包含累计误差的, 因此我们只能用T大致的估算t+1时刻的pose 为
然后, 我们可以基于观测来修正这个预测的pose.
航位推算在laserOdometry, laserMapping中用于计算配准优化的初始pose , 在transformMaintenance中为低频odom提供插值得到高频odom.
后面的伪代码部分, 有典型的航位推算位姿预测计算方式。
如果有使用LOAM基于其他类型的LiDAR运行的需求,那么必须弄清楚本段的内容。可以去Velodyne官网下载 配合阅读。
论文中称单个线束为一个Scan, 对全部16线组成的一帧点云称为一个Sweep,
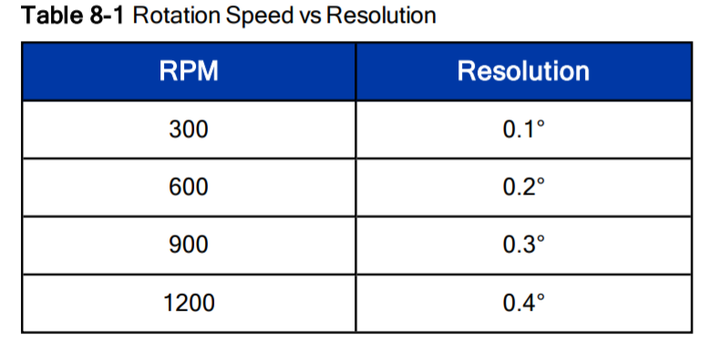
虽然是用的多线激光雷达,但是LOAM是针对单个Scan提取特征点的,这里**主要考虑到线束间角分辨率(竖直分辨率)与单个线内点间角分辨率(水平分辨率)存在的差异.**以VLP16为例, 竖直分辨率约为2°,而水平分辨率最大为0.4°(见下图).
**角分辨率越大, 代表越远的物体, 反射的两点距离越大, 中间丢失的信息越多.**因此, LOAM没有针对Scan和Scan之间的点的关联性提取和描述特征, 而是直接针对单个Scan提取特征.
LOAM的特征提取基于曲率,只提取两种特征点,corner和surface, 分别对应场景的平面区域和曲折区域.LOAM没有使用特征描述子(连曲率都没有参与后续的匹配).从代码中的corner与surface的曲率判断阈值可以看出,LOAM提取的corner和surface特征点的曲率, 并没有特别大的差别,这使得LOAM有较强的场景适应性,在场景中比较曲折的区域,corner点会占据主导,而在较为平缓的区域,surface点占据主导. 在激光扫描到的一块区域,总会提取出几个特征点。
要读懂代码中特征提取中的一些处理, 需要弄清楚VLP16扫描时的运动模型,简单的总结为:
一帧内所有的点, 都是按顺序穿行扫描的, 同一个时间点,只会有一次发送,紧接着一次接收。先从水平第一个角度,一般在0°左右,扫描这个水平角度上竖直方向所有16个点(对应16个SCAN)的深度,当然这16个点也是串行按顺序的,然后转到下一个水平角度, 比如0.3°开始, 水平分辨率0.4°,那么下个角度就是0.7°,然后1.1°.一直顺时针扫完一圈, 完成一个Sweep数据的采集.当然, Velodyne的User Manual里面讲的更清楚。
由于从驱动得到的一个Sweep是以点云的形式输出(也就是一堆点,每个点有XYZI的信息,点和点之间无其他关系信息), 因此我们并不知道每个点属于哪个Scan, 对应哪个水平角度,因此, 我们需要根据上面的扫描模型去计算每个点的竖直角度和水平角度.
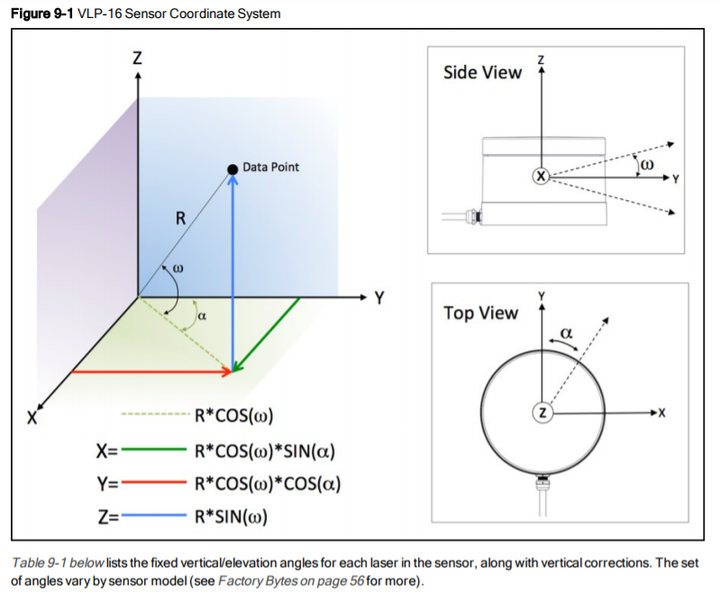
下图包含点坐标与竖直角度/水平角度的换算关系(来自):
对于竖直角度,可以用来查找这个点属于哪个Scan,我们将所有的点根据竖直角度分配到16个Scan中,每个Scan单独提取特征点。
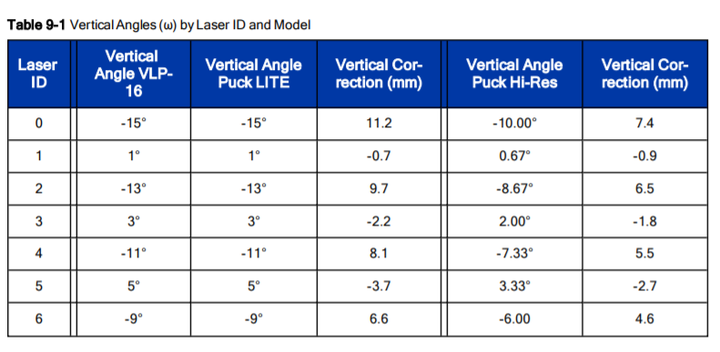
竖直角度与Scan的对应关系见下表(来自):
对于水平角度, 每个角度对应一个扫描的相对时间, 这在后续的运动补偿中用来去掉点云的畸变.
需要说明,每个Sweep不一定是从水平0°开始的, 大概是因为电机一直处于高速旋转中,没有一个复位的过程,雷达只在电机旋转到接近0°时记下当前对应激光点的精确坐标.同样,结束的位置,也不一定时0°.都是在0°周围.而第一个点和最后一个点的水平角度差也就不一定是2π, 而是接近2π的一个值, 有可能大于2π,这就带来了一定的复杂性.比如说,起始角度是0rad,结束角度是(2π+0.5)rad.而我们通过点的坐标计算其水平角度,如果得到的角度是0.25rad, 由于这是一个归一化的角度,可能是0.25rad,也可能是(0.25+2π)rad归一化得到的,那么这个激光点是开始的时候(0.25)扫描的, 还是结束的时候(0.25+2π)时扫描的?
当然上面的描述不够严谨, 实际归一化的角度是在[-π,π]范围内的.请参考代码理解。
所以, 光从点的3d(XYZ)位置, 有时是无法得到其精确的扫描时间的, 我们还需要结合时序信息,因为一个Sweep中返回的点是按时间顺序排列的,所以,时间靠前的0.25,就是一开始扫描的, 而时间靠后的0.25,就是最后扫描的0.25+2π.代码中用一个变量half_passed解决了此问题.对于其他型号的激光雷达, 只要理解了其每帧激光扫描的点顺序,就可以很容易的套用。
以VLP16为例,每一次激光扫描, 包含16条线, 每条线由1800个点组成,我们对每条线, 按照曲率提取特征点, 曲率的计算方式为:
a.每条SCAN的边缘5个点不参与特征点选取,因为周边不满足左右各五个点计算曲率的条件.
b.对任意点A, 选取左边五个点, 右边五个点, 共十个点.
c.每个点的x坐标与点A的x坐标求差, 将所有的差求和,得到sx
d.每个点y坐标与点A的y坐标求差, 将所有的差求和,得到sy
e.每个点的z坐标与点A的z坐标求差, 将所有的差求和,得到sz
计算完曲率, 就可以根据曲率挑选特征点, 为了使得在一周360度上有均匀的约束, 我们将一条激光线平均分为6块, 将块内的点按曲率大小排列,设置一个曲率阈值t, 比如t=0.1,来区分边缘点和平面点.我们设定一个每块的最大点数N。
边缘点选择条件:
从曲率最大的点开始,最多选择N个, 只有曲率大于t的点才能被选取
若一个点周围五个点中已有点被选为边缘点,跳过这个点, 从曲率更小的点中选取
平面点选择条件:
a.从曲率最小的点开始,最多选择N个, 只有曲率小于t的点才能被选取
b.若一个点周围五个点中已有点被选为平面点,跳过这个点, 从曲率更大的点中选取
针对corner点, 源码中取了两种N值,生成两份点云。分别称为corner_sharp 和corner less_sharp, corner_sharp取得N值偏小,所以选取的是曲率更大的几个点, 放到一个点云中。而corner_less_sharp选取的N值偏大, 选取更多的点,放到另一个点云中。
同样的道理, 针对surf点, 选取surf_flat和surf_less_flat两份点云。不过代码具体实施与corner略有不同。具体见代码, 此部分操作很简单, 不在赘述。
corner_less_sharp和surf_less_flat中包含更多的点,用来充当配准时的target, 而corner_sharp和surf_flat则充当source的角色。
此节点的功能在前面的节点简述-laserOdometry已有描述,其中运动补偿只是常规的运动补偿算法。特征点匹配以及优化部分的处理与laserMapping非常相似, 故我会在laserMapping中重点讲这部分,可以结合laserMapping中的逻辑来阅读和理解laserOdometry这部分。
如果要用LOAM实现一个定位算法,此部分除了运动补偿时必要的, 帧间匹配的ODOM并非必要, 完全可以用底盘编码器,视觉里程计或者IMU替代。帧间匹配ODOM的意义在于基于纯激光, 无任何外部输入, 也可以得到一个精度一般的ODOM。
需要说明下本部分的代码, 你可以看到源码中充斥着大量的IMU相关的变量和逻辑处理。实际上IMU只被当成一个ODOM,用于预测位姿, 以为后续的位姿优化提供初始位姿。所以:
(a) 用航位推算的思路去理解IMU相关代码
(b)可以尝试着将IMU的代码封装成一个predictWithIMU()的接口,整个代码会简单很多, 下一章亦然。
下面详述laserMapping节点的处理流程:
见“航位推算”这一段, 使用laserOdometry节点输出的ODOM预测位姿。
通过LiDAR在map坐标系中的位姿T,将LiDAR坐标系下的特征点转到map坐标系下.
针对map坐标系下的每个特征点,寻找与之接近的线或者面(corner对应线, surface对应面),
然后计算点与线/面的距离,这个距离就是该点对应的loss.
然后loss对位姿T求雅可比,使用高斯牛顿的方法,迭代优化T减小loss直到收敛。
基于位姿将特征点云分别拼接位corner地图和surface地图。只保留周围一定距离范围内的地图(一个圆柱,一个立方体,一个球体,都是OK的)。源码中是以立方体的形式。
paper中使用LM方法进行优化,而代码中使用的是高斯牛顿法.
paper中使用的是angle-axis进行优化,而代码中使用的是旋转矩阵直接对欧拉角求导,最终优
化的是欧拉角.
当然, 这不代表作者没有写基于LM优化angle-axis的代码。
(1) 点i在LiDAR坐标系下,k+1时刻的坐标.这里的点是指的特征点(corner点或者surface点)。
(2) 表示在世界坐标系下,k+1时刻,LiDAR的pose, 其中对应欧拉角在三个轴的转角, 这样表示是为了与代码对应.指的是平移部分.这个位姿是我们后续迭代优化的初始位姿,由上一帧位姿predict得到.在原始版本的代码中, predict基于匀速运动模型或者IMU数据实现,当然我们也可以使用其他的里程计(比如车轮编码器,或者视觉里程计)来实现.
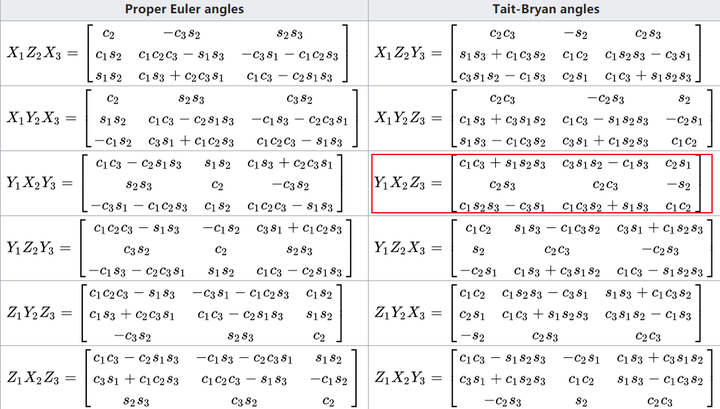
这里列出欧拉角对应的旋转矩阵:
(公式a)
见wikipedia 中的YXZ: https://en.wikipedia.org/wiki/Euler_angles 下图红框部分
平移向量:
(5) 表示一个corner点与匹配到的地图中的直线的距离,
一个surface点与匹配到的地图中的平面的距离,因为角点与平面点的过程基本一致, 后面统一用
表示.
构建单个特征点的loss function:
这个过程中, 需要通过 将
转换到map坐标系(因为原先特征点在LiDAR坐标系),我们定义这个函数为
:
(公式b)
已知世界坐标的点, 求其与地图中匹配直线的距离,我们定义这个函数为 :
(公式c)
故结合公式b,c
(公式d)
优化过程中,需要对每个分量的偏导,使用链式法则:
(公式e)
(公式f)
可见,对ex的偏导, 比对x的偏导, 多乘了一个部分:
而公共部分是:
结合公式bc得:
(公式g)
公式g中距离对点求导,可以理解为求一个点的变化(移动)方向,使得d减小的更快,也就是求, 点往哪个方向移动, 点到平面/直线的距离减小的更快?答案是沿着垂线方向.
故这部分, 针对corner点, 我们可以直接用点到与之匹配的直线之间的垂线方向对应的向量表示,针对surface点, 我们可以直接用点到与之匹配的平面之间的垂线方向对应的向量(也是平面的法向量)表示.
我们假设垂线方向对应的单位向量为), 其中 都可以通过简单的几何运算写为关于的表达式.
(公式h)
中间的3*3矩阵是公式a对x求偏导所得,此公式与代码中arx的计算一致。
本文不会再去推导非线性最小二乘问题的线性化和求解方法等问题,直接给出与代码相关部分的理论.
对于每个观测项,我们可以将线性化后的cost写为
(公式i)
其中 ,
(公式j)
其中 和
分别为每个观测项的雅可比矩阵和预测误差通过各个观测项的协方差矩阵
白化后的结果.
求解(公式i),代码中使用高斯牛顿法,通过求解normal equation, 我们可以得到高斯牛顿法的更新步长:
(公式k)
而且求解这个normal equation, 代码中使用了QR分解的方式,求得更新步长
我们将 叠加到之前的pose中, 然后重复点与地图匹配,建立cost function,求步长
,叠加
的过程直到收敛。
//lidar坐标系:x轴向前,y轴向左,z轴向上的右手坐标系
//处理频率:与激光帧率一致
void FeatureDt::getFeaturePoints(pcl::PointCloud<PointType> &laser_cloud_in,
uint64_t ts,
pcl::PointCloud<PointType>::Ptr &laser_cloud_in_range,
pcl::PointCloud<PointType>::Ptr &corner_sharp,
pcl::PointCloud<PointType>::Ptr &corner_less_sharp,
pcl::PointCloud<PointType>::Ptr &surf_flat,
pcl::PointCloud<PointType>::Ptr &surf_less_flat)
{
int cloud_in_size = laser_cloud_in.points.size();
//获取点云的开始和结束水平角度, 确定一帧中点的角度范围
//此处需要注意一帧扫描角度不一定<2pi, 可能大于2pi, 角度需特殊处理
//角度范围用于确定每个点的相对扫描时间, 用于运动补偿
float start_yaw;
float end_yaw;
getYawRange(laser_cloud_in, cloud_in_size, start_yaw, end_yaw);
//至于此处half_passed的作用, 文中有详述
bool half_passed = false;
int cloud_filted_size = cloud_in_size;
PointType point;
//每一线存储为一个单独的线(SCAN), 针对单个线计算特征点
std::vector<PointCloudType> laser_cloud_per_scan(N_SCANS);
//把点根据几何角度(竖直)分配到线中
for (int i = 0; i < cloud_in_size; i++)
{
point.x = laser_cloud_in.points[i].x;
point.y = laser_cloud_in.points[i].y;
point.z = laser_cloud_in.points[i].z;
//scan_id由竖直角度映射而得, 具体参考lidar的user manual
int scan_id = getScanIDOfPoint(point);
if (scan_id > (N_SCANS - 1) || scan_id < 0)
{
cloud_filted_size--;
continue;
}
float point_yaw;
getYawOfOnePoint(start_yaw, end_yaw, point, point_yaw, half_passed);
//计算此点在此帧中扫描的相对时间, 用来作为后续的运动补偿
float yaw_percent = (point_yaw - start_yaw) / (end_yaw - start_yaw);
//复用这个字段传递参数,整数部分是SCANID, 小数部分是相对时间
point.intensity = toIntensity(scan_id, yaw_percent);
//往对应的scan中, 新增一个point
laser_cloud_per_scan[scan_id].push_back(point);
}
//将点云按scan顺序排列, 重新组成大点云
for (int i = 0; i < N_SCANS; i++)
{
*laser_cloud_in_range += laser_cloud_per_scan[i];
}
//记录每个scanid的开始和结束点
std::vector<int> scan_start_ind(N_SCANS, 0);
std::vector<int> scan_end_ind(N_SCANS, 0);
calcCurvature(laser_cloud_in_range, cloud_filted_size, scan_start_ind, scan_end_ind);
detectFeaturePoint(laser_cloud_in_range, cloud_filted_size, scan_start_ind, scan_end_ind, corner_sharp, corner_less_sharp, surf_flat, surf_less_flat);
}
//这三个函数涉及服用点云中点的intersity字段,存储scanid(intensity的整数部分)和相对扫描时间(intensity小数部分)
inline float toIntensity(int scanID, float yawPercent)
{
return scanID + yawPercent;
}
inline int toScanID(float intensity)
{
return int(intensity);
}
inline float toReltiveTime(float intensity)
{
return intensity - int(intensity);
}
void FeatureDt::getYawRange(pcl::PointCloud<PointType> &laser_cloud_in,
int cloud_size,
float &start_yaw, float &end_yaw
)
{
//第一个点和最后一个点对应的是第一和最末一束线
//velodyne是顺时针增大, 而坐标轴中的yaw是逆时针增加, 所以这里要取负号
start_yaw = -atan2(laser_cloud_in.points[0].y, laser_cloud_in.points[0].x);
end_yaw = -atan2(laser_cloud_in.points[cloud_size - 1].y, laser_cloud_in.points[cloud_size - 1].x) + 2 * M_PI;
//atan2得到的角度是[-pi, pi], 所以, 如果都用标准化的角度, 那么end_yaw可能小于或者接近start_yaw, 这不利于后续的运动补偿
//因为运动补偿需要从每个点的水平角度确定其在一帧中的相对时间
//我们需要转换到end_yaw > start_yaw 且end_yaw-start_yaw接近2*M_PI的形式, 所以就有了以下代码
if (end_yaw - start_yaw > 3 * M_PI)
{
end_yaw -= 2 * M_PI;
}
else if (end_yaw - start_yaw < M_PI)
{
end_yaw += 2 * M_PI;
}
}
//yaw决定了点的相对扫描时间
void FeatureDt::getYawOfOnePoint(float &start_yaw,
float &end_yaw,
PointType point,
float &yaw,
bool &half_passed
)
{
yaw = -atan2(point.y, point.x);
//因为转一圈可能会超过2pi, 故角度a可能对应a或者2pi + a
//如何确定是a还是2pi+a呢, half_passed 利用点的顺序与时间先后相关这一点解决了这个问题
if (!half_passed)
{
if (yaw < start_yaw - M_PI / 2)
{
yaw += 2 * M_PI;
}
else if (yaw > start_yaw + M_PI * 3 / 2)
{
yaw -= 2 * M_PI;
}
if (yaw - start_yaw > M_PI)
{
half_passed = true;
}
}
else
{
yaw += 2 * M_PI;
if (yaw < end_yaw - M_PI * 3 / 2)
{
yaw += 2 * M_PI;
}
else if (yaw > end_yaw + M_PI / 2)
{
yaw -= 2 * M_PI;
}
}
}
//计算曲率
void FeatureDt::calcCurvature(pcl::PointCloud<PointType>::Ptr laser_cloud,
int cloud_size,
std::vector<int> &scan_start_ind,
std::vector<int> &scan_end_ind
)
{
int scan_count = -1;
//针对每个点求其特征
for (int i = 5; i < cloud_size - 5; i++)
{
//用周围的10个点计算其描述子, 边界的点省略掉, 因为他们周围的点不足5个
float diff_x = laser_cloud->points[i - 5].x + laser_cloud->points[i - 4].x + laser_cloud->points[i - 3].x + laser_cloud->points[i - 2].x + laser_cloud->points[i - 1].x - 10 * laser_cloud->points[i].x + laser_cloud->points[i + 1].x + laser_cloud->points[i + 2].x + laser_cloud->points[i + 3].x + laser_cloud->points[i + 4].x + laser_cloud->points[i + 5].x;
float diff_y = laser_cloud->points[i - 5].y + laser_cloud->points[i - 4].y + laser_cloud->points[i - 3].y + laser_cloud->points[i - 2].y + laser_cloud->points[i - 1].y - 10 * laser_cloud->points[i].y + laser_cloud->points[i + 1].y + laser_cloud->points[i + 2].y + laser_cloud->points[i + 3].y + laser_cloud->points[i + 4].y + laser_cloud->points[i + 5].y;
float diff_z = laser_cloud->points[i - 5].z + laser_cloud->points[i - 4].z + laser_cloud->points[i - 3].z + laser_cloud->points[i - 2].z + laser_cloud->points[i - 1].z - 10 * laser_cloud->points[i].z + laser_cloud->points[i + 1].z + laser_cloud->points[i + 2].z + laser_cloud->points[i + 3].z + laser_cloud->points[i + 4].z + laser_cloud->points[i + 5].z;
//曲率计算公式
cloud_curvature_[i] = diff_x * diff_x + diff_y * diff_y + diff_z * diff_z;
cloud_sort_ind_[i] = i;
//特征点默认为less_smooth, 后续会在曲率筛选中改变这个label
//neighbor_picked意义在于,当一个点被选为corner或者surf时, 周边N个点不要被选, 让特征点尽量分布广, 不聚集
cloud_neighbor_picked_[i] = 0;
cloud_label_[i] = CURV_LESS_SMOOTH;
if (toScanID(laser_cloud->points[i].intensity) != scan_count)
{
scan_count = toScanID(laser_cloud->points[i].intensity);
if (scan_count > 0 && scan_count < N_SCANS)
{
//设置本scan的头
scan_start_ind[scan_count] = i + 5;
//设置上个scan的尾
scan_end_ind[scan_count - 1] = i - 5;
}
}
}
//最前和最后5个点不方便计算曲率, 抛弃
//不要认为一个SCAN首尾可以相接, 运动状态导致的畸变会使得首尾差距很大
scan_start_ind[0] = 5;
scan_end_ind.back() = cloud_size - 5;
//paper中(a) (b)这两种特殊情况的点不会被选为corner orsurface
for (int i = 5; i < cloud_size - 6; i++)
{
//计算曲率
float diff_x = laser_cloud->points[i + 1].x - laser_cloud->points[i].x;
float diff_y = laser_cloud->points[i + 1].y - laser_cloud->points[i].y;
float diff_z = laser_cloud->points[i + 1].z - laser_cloud->points[i].z;
float diff = diff_x * diff_x + diff_y * diff_y + diff_z * diff_z;
//曲率阈值过滤
if (diff > 0.1)
{
float depth1 = sqrt(laser_cloud->points[i].x * laser_cloud->points[i].x +
laser_cloud->points[i].y * laser_cloud->points[i].y +
laser_cloud->points[i].z * laser_cloud->points[i].z);
float depth2 = sqrt(laser_cloud->points[i + 1].x * laser_cloud->points[i + 1].x +
laser_cloud->points[i + 1].y * laser_cloud->points[i + 1].y +
laser_cloud->points[i + 1].z * laser_cloud->points[i + 1].z);
//针对paper中(b)情况
if (depth1 > depth2)
{
diff_x = laser_cloud->points[i + 1].x - laser_cloud->points[i].x * depth2 / depth1;
diff_y = laser_cloud->points[i + 1].y - laser_cloud->points[i].y * depth2 / depth1;
diff_z = laser_cloud->points[i + 1].z - laser_cloud->points[i].z * depth2 / depth1;
if (sqrt(diff_x * diff_x + diff_y * diff_y + diff_z * diff_z) / depth2 < 0.1)
{
cloud_neighbor_picked_[i - 5] = 1;
cloud_neighbor_picked_[i - 4] = 1;
cloud_neighbor_picked_[i - 3] = 1;
cloud_neighbor_picked_[i - 2] = 1;
cloud_neighbor_picked_[i - 1] = 1;
cloud_neighbor_picked_[i] = 1;
}
}
else
{
diff_x = laser_cloud->points[i + 1].x * depth1 / depth2 - laser_cloud->points[i].x;
diff_y = laser_cloud->points[i + 1].y * depth1 / depth2 - laser_cloud->points[i].y;
diff_z = laser_cloud->points[i + 1].z * depth1 / depth2 - laser_cloud->points[i].z;
if (sqrt(diff_x * diff_x + diff_y * diff_y + diff_z * diff_z) / depth1 < 0.1)
{
cloud_neighbor_picked_[i + 1] = 1;
cloud_neighbor_picked_[i + 2] = 1;
cloud_neighbor_picked_[i + 3] = 1;
cloud_neighbor_picked_[i + 4] = 1;
cloud_neighbor_picked_[i + 5] = 1;
cloud_neighbor_picked_[i + 6] = 1;
}
}
}
//针对paper中(a)情况
float diff_x_2 = laser_cloud->points[i].x - laser_cloud->points[i - 1].x;
float diff_y_2 = laser_cloud->points[i].y - laser_cloud->points[i - 1].y;
float diff_z_2 = laser_cloud->points[i].z - laser_cloud->points[i - 1].z;
float diff_2 = diff_x_2 * diff_x_2 + diff_y_2 * diff_y_2 + diff_z_2 * diff_z_2;
float dis = laser_cloud->points[i].x * laser_cloud->points[i].x + laser_cloud->points[i].y * laser_cloud->points[i].y + laser_cloud->points[i].z * laser_cloud->points[i].z;
if (diff > 0.0002 * dis && diff_2 > 0.0002 * dis)
{
cloud_neighbor_picked_[i] = 1;
}
}
}
void FeatureDt::detectFeaturePoint(pcl::PointCloud<PointType>::Ptr laser_cloud,
int cloud_size,
std::vector<int> &scan_start_ind,
std::vector<int> &scan_end_ind,
pcl::PointCloud<PointType>::Ptr &corner_sharp,
pcl::PointCloud<PointType>::Ptr &corner_less_sharp,
pcl::PointCloud<PointType>::Ptr &surf_flat,
pcl::PointCloud<PointType>::Ptr &surf_less_flat)
{
//还是每束scan单独处理
for (int i = 0; i < N_SCANS; i++)
{
pcl::PointCloud<PointType>::Ptr surf_points_less_flat_scan(new pcl::PointCloud<PointType>);
int less_sharp_num = 0;
//将每个线等分为六段,分别进行处理(sp、ep分别为各段的起始和终止位置)
for (int j = 0; j < 6; j++)
{
//先求每段的开始和结束点
int sp = (scan_start_ind[i] * (6 - j) + scan_end_ind[i] * j) / 6;
int ep = (scan_start_ind[i] * (5 - j) + scan_end_ind[i] * (j + 1)) / 6 - 1;
//在每一段,排序, 小的在前, 大的在后
for (int k = sp + 1; k <= ep; k++)
{
for (int l = k; l >= sp + 1; l--)
{
if (cloud_curvature_[cloud_sort_ind_[l]] < cloud_curvature_[cloud_sort_ind_[l - 1]])
{
swap(cloud_sort_ind_[l - 1], cloud_sort_ind_[l]);
}
}
}
//选取角点
int largest_picked_num = 0;
for (int k = ep; k >= sp; k--)
{
//k = ep, cloud_sort_ind_[k]对应这一组最末位置的index, 也就是曲率最大的index
int ind = cloud_sort_ind_[k];
//如果邻居没被选中并且自己够格
if (cloud_neighbor_picked_[ind] == 0 && cloud_curvature_[ind] > 0.1)
{
largest_picked_num++;
//取x个认为是sharp的点
if (largest_picked_num <= 6)
{
cloud_label_[ind] = CURV_SHARP;
corner_sharp->push_back(laser_cloud->points[ind]);
corner_less_sharp->push_back(laser_cloud->points[ind]);
less_sharp_num++;
}
//取y个认为是lesssharp的点
else if (largest_picked_num <= 24)
{
cloud_label_[ind] = CURV_LESS_SHARP;
corner_less_sharp->push_back(laser_cloud->points[ind]);
less_sharp_num++;
}
else
{
break;
}
//选中的点标记为已选
cloud_neighbor_picked_[ind] = 1;
//向后五个点
for (int l = 1; l <= 5; l++)
{
//之前的曲率是前后各五个点, 这里计算相邻两点的变化率
float diff_x = laser_cloud->points[ind + l].x - laser_cloud->points[ind + l - 1].x;
float diff_y = laser_cloud->points[ind + l].y - laser_cloud->points[ind + l - 1].y;
float diff_z = laser_cloud->points[ind + l].z - laser_cloud->points[ind + l - 1].z;
//遇到某点曲率高不标记, 还有机会被选上
if (diff_x * diff_x + diff_y * diff_y + diff_z * diff_z > 0.05)
{
break;
}
//否则, 标记, 因为邻居是角点, 你不能再做角点
cloud_neighbor_picked_[ind + l] = 1;
}
//向前五个点, 逻辑用上
for (int l = -1; l >= -5; l--)
{
float diff_x = laser_cloud->points[ind + l].x - laser_cloud->points[ind + l + 1].x;
float diff_y = laser_cloud->points[ind + l].y - laser_cloud->points[ind + l + 1].y;
float diff_z = laser_cloud->points[ind + l].z - laser_cloud->points[ind + l + 1].z;
if (diff_x * diff_x + diff_y * diff_y + diff_z * diff_z > 0.05)
{
break;
}
cloud_neighbor_picked_[ind + l] = 1;
}
}
}
//选取平面点
int smallest_picked_num = 0;
for (int k = sp; k <= ep; k++)
{
//!! k = sp, cloud_sort_ind_[k]对应这一组最先位置的index, 也就是曲率最小的index
int ind = cloud_sort_ind_[k];
if (cloud_neighbor_picked_[ind] == 0 && cloud_curvature_[ind] < 0.1)
{
cloud_label_[ind] = CURV_SMOOTH;
surf_flat->push_back(laser_cloud->points[ind]);
smallest_picked_num++;
if (smallest_picked_num >= 8)
{
break;
}
//已选中的点, 对临近点进行标记
cloud_neighbor_picked_[ind] = 1;
//向后遍历五个点
for (int l = 1; l <= 5; l++)
{
float diff_x = laser_cloud->points[ind + l].x - laser_cloud->points[ind + l - 1].x;
float diff_y = laser_cloud->points[ind + l].y - laser_cloud->points[ind + l - 1].y;
float diff_z = laser_cloud->points[ind + l].z - laser_cloud->points[ind + l - 1].z;
//此处发生突变, 停止标记临近点
if (diff_x * diff_x + diff_y * diff_y + diff_z * diff_z > 0.05)
{
break;
}
cloud_neighbor_picked_[ind + l] = 1;
}
//向前遍历五个点, 逻辑同上
for (int l = -1; l >= -5; l--)
{
float diff_x = laser_cloud->points[ind + l].x - laser_cloud->points[ind + l + 1].x;
float diff_y = laser_cloud->points[ind + l].y - laser_cloud->points[ind + l + 1].y;
float diff_z = laser_cloud->points[ind + l].z - laser_cloud->points[ind + l + 1].z;
if (diff_x * diff_x + diff_y * diff_y + diff_z * diff_z > 0.05)
{
break;
}
cloud_neighbor_picked_[ind + l] = 1;
}
}
}
//取平面点 less smooth, 之前没被选中的都会被标记为less smooth
for (int k = sp; k <= ep; k++)
{
// <= CURV_LESS_SMOOTH means smooth or less smooth
if (cloud_label_[k] <= CURV_LESS_SMOOTH)
{
surf_points_less_flat_scan->push_back(laser_cloud->points[k]);
}
}
}
// 对lessFlatScan进行降采样
pcl::PointCloud<PointType> surf_points_less_flat_scan_ds;
pcl::VoxelGrid<PointType> down_size_filter;
down_size_filter.setInputCloud(surf_points_less_flat_scan);
down_size_filter.setLeafSize(0.15, 0.15, 0.15);
down_size_filter.filter(surf_points_less_flat_scan_ds);
//sp 是个step, 这里使用了一种简单的点过滤方法
int sp = 1;
if (less_sharp_num == 0)
{
sp = floor(1.0 * surf_points_less_flat_scan_ds.size() / 100);
}
else
{
sp = floor(1.0 * surf_points_less_flat_scan_ds.size() / less_sharp_num / 3);
}
sp = sp > 0 ? sp : 1;
for (int k = 0; k < surf_points_less_flat_scan_ds.size(); k += sp)
{
surf_less_flat->push_back(surf_points_less_flat_scan_ds.points[k]);
}
}
}
int FeatureDt::getScanIDOfPoint(PointType &point)
{
//线与水平面的夹角,计算线束的角度, 以确定属于哪条线, 单位 °
float scan_pitch = atan(point.z / sqrt(point.x * point.x + point.y * point.y)) * 180 / M_PI;
//根据scanPitch确定scan ID, 范围0~N_SCANS - 1, scanID在后面寻找最近直线时将发挥重要作用
int rounded_scan_pitch = int(scan_pitch / 2.0 + (scan_pitch < 0.0 ? -0.5 : +0.5));
int scan_id = 0;
//让SCANID在物理上连续
scan_id = rounded_scan_pitch + 7;
return scan_id;
}
laserMapping
void LaMapping::solveWithGaussNewton(cv::Mat &mat_x,
int iter_count,
pcl::PointCloud<PointType>::Ptr points_selected
pcl::PointCloud<PointType>::Ptr coeff_selected)
{
int laser_cloud_sel_num = points_selected->size();
bool is_degenerate = false;
cv::Mat mat_p(6, 6, CV_32F, cv::Scalar::all(0));
//预先计算三个欧拉角的sin 和cos, 对应文章中的sin(ex), cos(ex),
//sin(ey), cos(ey), sin(ez), cos(ez),
float srx = sin(lidar_pose_in_map_r_[0]);
float crx = cos(lidar_pose_in_map_r_[0]);
float sry = sin(lidar_pose_in_map_r_[1]);
float cry = cos(lidar_pose_in_map_r_[1]);
float srz = sin(lidar_pose_in_map_r_[2]);
float crz = cos(lidar_pose_in_map_r_[2]);
//高斯牛顿求解中用到的一些矩阵, 对应正规方程(normal equation), AT*A*x = AT*b
cv::Mat mat_a(laser_cloud_sel_num, 6, CV_32F, cv::Scalar::all(0));
cv::Mat mat_a_t(6, laser_cloud_sel_num, CV_32F, cv::Scalar::all(0));
cv::Mat mat_a_t_a(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat mat_b(laser_cloud_sel_num, 1, CV_32F, cv::Scalar::all(0));
cv::Mat mat_a_t_b(6, 1, CV_32F, cv::Scalar::all(0));
//将每个观测项构建最小二乘问题, 公式i
for (int i = 0; i < laser_cloud_sel_num; i++)
{
PointType point_ori, coeff;
point_ori = points_selected->points[i];
coeff = coeff_selected->points[i];
//coeff.x, coeff.y, coeff.z 为loss对pose中x, y, z的偏导
//coeff.intensity 为loss
//以下代码中的arx计算对应公式h
float arx = (crx * sry * srz * point_ori.x + crx * crz * sry * point_ori.y - srx * sry * point_ori.z) * coeff.x
+ (-srx * srz * point_ori.x - crz * srx * point_ori.y - crx * point_ori.z) * coeff.y
+ (crx * cry * srz * point_ori.x + crx * cry * crz * point_ori.y - cry * srx * point_ori.z) * coeff.z;
float ary = ((cry * srx * srz - crz * sry) * point_ori.x + (sry * srz + cry * crz * srx) * point_ori.y + crx * cry * point_ori.z) * coeff.x
+ ((-cry * crz - srx * sry * srz) * point_ori.x + (cry * srz - crz * srx * sry) * point_ori.y - crx * sry * point_ori.z) * coeff.z;
float arz = ((crz * srx * sry - cry * srz) * point_ori.x + (-cry * crz - srx * sry * srz) * point_ori.y) * coeff.x
+ (crx * crz * point_ori.x - crx * srz * point_ori.y) * coeff.y
+ ((sry * srz + cry * crz * srx) * point_ori.x + (crz * sry - cry * srx * srz) * point_ori.y) * coeff.z;
//见公式i
mat_a.at<float>(i, 0) = arx;
mat_a.at<float>(i, 1) = ary;
mat_a.at<float>(i, 2) = arz;
mat_a.at<float>(i, 3) = coeff.x;
mat_a.at<float>(i, 4) = coeff.y;
mat_a.at<float>(i, 5) = coeff.z;
mat_b.at<float>(i, 0) = -coeff.intensity;
}
//构建normal equation, 见公式k
cv::transpose(mat_a, mat_a_t);
mat_a_t_a = mat_a_t * mat_a;
mat_a_t_b = mat_a_t * mat_b;
//高斯牛顿法, 直接解normal equation求步长, QR分解是一种解法
cv::solve(mat_a_t_a, mat_a_t_b, mat_x, cv::DECOMP_QR);
//具体描述见Loam作者Zhang J的<<On Degeneracy of Optimization-based State Estimation Problems>>
//大概方法是通过Jacobian的eigenvalue判断哪个分量的约束不足, 不更新那个方向上的迭代
if (iter_count == 0)
{
cv::Mat mat_e(1, 6, CV_32F, cv::Scalar::all(0));
cv::Mat mat_v(6, 6, CV_32F, cv::Scalar::all(0));
cv::Mat mat_v2(6, 6, CV_32F, cv::Scalar::all(0));
cv::eigen(mat_a_t_a, mat_e, mat_v);
mat_v.copyTo(mat_v2);
is_degenerate = false;
float eign_thre[6] = {100, 100, 100, 100, 100, 100};
for (int i = 5; i >= 0; i--)
{
if (mat_e.at<float>(0, i) < eign_thre[i])
{
for (int j = 0; j < 6; j++)
{
mat_v2.at<float>(i, j) = 0;
}
is_degenerate = true;
}
else
{
break;
}
}
mat_p = mat_v.inv() * mat_v2;
}
if (is_degenerate)
{
cv::Mat mat_x2(6, 1, CV_32F, cv::Scalar::all(0));
mat_x.copyTo(mat_x2);
mat_x = mat_p * mat_x2;
}
}
//更新迭代的结果
void LaMapping::updateTransformFromOptimize(cv::Mat &mat_x)
{
lidar_pose_in_map_r_[0] += mat_x.at<float>(0, 0);
lidar_pose_in_map_r_[1] += mat_x.at<float>(1, 0);
lidar_pose_in_map_r_[2] += mat_x.at<float>(2, 0);
lidar_pose_in_map_t_[0] += mat_x.at<float>(3, 0);
lidar_pose_in_map_t_[1] += mat_x.at<float>(4, 0);
lidar_pose_in_map_t_[2] += mat_x.at<float>(5, 0);
}
bool LaMapping::isConverged(cv::Mat &mat_x)
{
//判断是否已收敛, 这里的判断方法很简单
float delta_r = sqrt(
pow(radToDeg(mat_x.at<float>(0, 0)), 2) +
pow(radToDeg(mat_x.at<float>(1, 0)), 2) +
pow(radToDeg(mat_x.at<float>(2, 0)), 2));
float delta_t = sqrt(
pow(mat_x.at<float>(3, 0) * 100, 2) +
pow(mat_x.at<float>(4, 0) * 100, 2) +
pow(mat_x.at<float>(5, 0) * 100, 2));
return (delta_r < 0.1 && delta_t < 0.3);
}
void LaMapping::doOptimize(int max_iteration)
{
//复用point cloud结构存储偏导数,
pcl::PointCloud<PointType>::Ptr coeff_selected boost::make_shared<pcl::PointCloud<PointType>>();
//存储匹配成功的点,与coeff_selected一一对应
pcl::PointCloud<PointType>::Ptr points_selected boost::make_shared<pcl::PointCloud<PointType>>();
//限制迭代次数
for (int iter_count = 0; iter_count < max_iteration; iter_count++)
{
//分别处理corner特征和feature特征, 建立loss成功的点(以下称为有效点), 会加入到features_selected
//可以见到, 每次迭代, 我们会重新做一次特征点匹配
procLossAboutCornerPoints(corner_feature_points, points_selected, coeff_selected);
procLossAboutSurfPoints(surf_feature_points, points_selected, coeff_selected);
//如果有效点数小于特定值, 我们认为约束不够, 放弃此次优化
//无法优化的话, 会直接使用pose的预测值
if (points_selected()->size() < features_slected_num_enough_for_optimize)
{
break;
}
cv::Mat mat_x(6, 1, CV_32F, cv::Scalar::all(0));
//构建norm equation, 求解pose增量
solveWithGaussNewton(mat_x, iter_count, points_selected, coeff_selected);
//根据高斯牛顿迭代结果, 更新pose
updateTransformFromOptimize(mat_x);
if (isConverged(mat_x))
{
//如果迭代趋于收敛, 退出
break;
}
}
}
void LaMapping::procLossAboutSurfPoints(pcl::PointCloud<PointType>::Ptr surf_feature_points,
pcl::PointCloud<PointType>::Ptr points_selected,
pcl::PointCloud<PointType>::Ptr coeff_selected
)
{
for (int i = 0; i < surf_feature_points->size(); i++)
{
//将点转换到世界坐标系
PointType point_sel = transPointToMapCoordinate(surf_feature_points[i]);
std::vector<int> point_search_ind;
std::vector<float> point_search_sq_dis;
//从map对应的kdtree中, 搜索半径一米内的五个surf特征点
if (surf_kdtree_ptr->radiusSearch(point_sel, 1.0, point_search_ind, point_search_sq_dis, 5) < 5)
{
//没有搜到足够多的点, 本点匹配失败, 此点不对后续的优化贡献约束
continue;
}
//这些变量用来求解平面方程, 平面方程为AX+BY+CZ+D = 0 <=> AX+BY+CZ=-D <=> (A/D)X+(B/D)Y+(C/D)Z = -1
//其中(X,Y,Z)是点的坐标, 对应这里的mat_a0, 是已知数
//A/D, B/D, C/D 对应mat_x0, 是待求的值
//等式右边的-1对应mat_b0
cv::Mat mat_a0(5, 3, CV_32F, cv::Scalar::all(0));
cv::Mat mat_b0(5, 1, CV_32F, cv::Scalar::all(-1));
cv::Mat mat_x0(3, 1, CV_32F, cv::Scalar::all(0));
//构建五个最近点的坐标矩阵
for (int j = 0; j < 5; j++)
{
mat_a0.at<float>(j, 0) = map_ptr->points[point_search_ind[j]].x;
mat_a0.at<float>(j, 1) = map_ptr->points[point_search_ind[j]].y;
mat_a0.at<float>(j, 2) = map_ptr->points[point_search_ind[j]].z;
}
//求解 (A/D)X+(B/D)Y+(C/D)Z = -1 中的 A/D, B/D, C/D
cv::solve(mat_a0, mat_b0, mat_x0, cv::DECOMP_QR);
float pa = mat_x0.at<float>(0, 0);
float pb = mat_x0.at<float>(1, 0);
float pc = mat_x0.at<float>(2, 0);
//对应之前的-1, (A/D)X+(B/D)Y+(C/D)Z = -1 <=> (A/D)X+(B/D)Y+(C/D)Z +1 = 0
float pd = 1;
//ps为平面法向量的模
//求得(pa, pb, pc)为法向量, 模为1, pd为平面到原点的距离
float ps = sqrt(pa * pa + pb * pb + pc * pc);
pa /= ps;
pb /= ps;
pc /= ps;
pd /= ps;
//确定拟合出的平面与用来拟合的点都足够接近, 表示平面拟合的有效性
bool plane_valid = false;
for (int j = 0; j < 5; j++)
{
if (fabs(pa * map_ptr->points[point_search_ind[j]].x +
pb * map_ptr->points[point_search_ind[j]].y +
pc * map_ptr->points[point_search_ind[j]].z + pd) > 0.2)
{
plane_valid = true;
break;
}
}
if(plane_valid)
{
//平面无效, 本点匹配失败, 此点不对后续的优化贡献约束
continue;
}
//点到平面的距离, 参考点到平面距离公式, 分母部分为1
float pd2 = pa * point_sel.x + pb * point_sel.y + pc * point_sel.z + pd;
//这里的s是个权重, 表示s在这个least-square问题中的置信度, 每个点的置信度不一样
//理论上, 这个权重, 与点到面距离负相关, 距离越大, 置信度越低, 这里相当于是一个在loss之外加了一个鲁棒性函数, 用来过减弱离群值的影响
//源代码中"sqrt(sqrt(point_sel.x * point_sel.x + point_sel.y * point_sel.y + point_sel.z * point_sel.z)" 这部分, 并没有什么逻辑性可言
//你可以设计自己的鲁棒性函数来替代这一行代码
float s = 1 - 0.9 * fabs(pd2) / sqrt(sqrt(point_sel.x * point_sel.x + point_sel.y * point_sel.y + point_sel.z * point_sel.z));
//最终确定的可优化点
if (s > 0.1)
{
points_selected.push_back(point_sel);
//复用PointType传递偏导数, (pa, pb, pc)是法向量,点到平面的垂线, 也是点面距离相对与点坐标的偏导, 详见文章的公式推导部分.
//pd2是loss
PointType coeff;
coeff.x = s * pa;
coeff.y = s * pb;
coeff.z = s * pc;
coeff.intensity = s * pd2;
coeff_selected.push_back(corner_feature_points[i]);
}
else
{
//距离无效, 本点匹配失败, 此点不对后续的优化贡献约束
}
}
}
void LaMapping::procLossAboutCornerPoints(pcl::PointCloud<PointType>::Ptr corner_feature_points,
pcl::PointCloud<PointType>::Ptr points_selected,
pcl::PointCloud<PointType>::Ptr coeff_selected
)
{
for (int i = 0; i < corner_feature_points->size(); i++)
{
//将点转换到世界坐标系
PointType point_sel = transPointToMapCoordinate(corner_feature_points[i]);
std::vector<int> point_search_ind;
std::vector<float> point_search_sq_dis;
//从map对应的kdtree中, 搜索半径一米内的五个corner特征点
if (surf_kdtree_ptr->radiusSearch(point_sel, 1.0, point_search_ind, point_search_sq_dis, 5) < 5)
{
//没有搜到足够多的点, 本点匹配失败, 此点不对后续的优化贡献约束
continue;
}
//将五个最近点的坐标加和求平均
float cx = 0;
float cy = 0;
float cz = 0;
cv::Mat mat_a1(3, 3, CV_32F, cv::Scalar::all(0));
cv::Mat mat_d1(1, 3, CV_32F, cv::Scalar::all(0));
cv::Mat mat_v1(3, 3, CV_32F, cv::Scalar::all(0));
for (int j = 0; j < 5; j++)
{
cx += corner_map->points[point_search_ind[j]].x;
cy += corner_map->points[point_search_ind[j]].y;
cz += corner_map->points[point_search_ind[j]].z;
}
//坐标均值
cx /= 5;
cy /= 5;
cz /= 5;
//求均方差
float a11 = 0;
float a12 = 0;
float a13 = 0;
float a22 = 0;
float a23 = 0;
float a33 = 0;
for (int j = 0; j < 5; j++)
{
float ax = corner_map->points[point_search_ind[j]].x - cx;
float ay = corner_map->points[point_search_ind[j]].y - cy;
float az = corner_map->points[point_search_ind[j]].z - cz;
a11 += ax * ax;
a12 += ax * ay;
a13 += ax * az;
a22 += ay * ay;
a23 += ay * az;
a33 += az * az;
}
//协方差矩阵的6个元素(3*3矩阵, 对角元素重复)
a11 /= 5;
a12 /= 5;
a13 /= 5;
a22 /= 5;
a23 /= 5;
a33 /= 5;
//构建协方差矩阵
mat_a1.at<float>(0, 0) = a11;
mat_a1.at<float>(0, 1) = a12;
mat_a1.at<float>(0, 2) = a13;
mat_a1.at<float>(1, 0) = a12;
mat_a1.at<float>(1, 1) = a22;
mat_a1.at<float>(1, 2) = a23;
mat_a1.at<float>(2, 0) = a13;
mat_a1.at<float>(2, 1) = a23;
mat_a1.at<float>(2, 2) = a33;
//对协方差矩阵进行Eigenvalue decomposition, 以分析空间点的分布规律
cv::eigen(mat_a1, mat_d1, mat_v1);
//如果最大特征值相对第二大特征值的比例足够大, 那么反应点的分布趋于一条直线
if (mat_d1.at<float>(0, 0) > 3 * mat_d1.at<float>(0, 1))
{
//(x0, y0, z0)世界坐标系下的特征点
float x0 = point_sel.x;
float y0 = point_sel.y;
float z0 = point_sel.z;
//(x1,y1,z1), (x2,y2,z2) 用来表示特征值最大方向对应的直线
float x1 = cx + 0.1 * mat_v1.at<float>(0, 0);
float y1 = cy + 0.1 * mat_v1.at<float>(0, 1);
float z1 = cz + 0.1 * mat_v1.at<float>(0, 2);
float x2 = cx - 0.1 * mat_v1.at<float>(0, 0);
float y2 = cy - 0.1 * mat_v1.at<float>(0, 1);
float z2 = cz - 0.1 * mat_v1.at<float>(0, 2);
//a012为点到直线距离计算分子部分
//两向量的叉乘
float a012 = sqrt(((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1))
* ((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1))
+ ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1))
* ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1))
+ ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1))
* ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1)));
//l12为点到直线距离公式分母部分,(x1,y1,z1), (x2,y2,z2)两点的距离
float l12 = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2) + (z1 - z2) * (z1 - z2));
//(la, lb, lc)为单位向量, 模为1 ,方向为从垂足->点p
float la = ((y1 - y2) * ((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1)) + (z1 - z2) * ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1))) / a012 / l12;
float lb = -((x1 - x2) * ((x0 - x1) * (y0 - y2) - (x0 - x2) * (y0 - y1)) - (z1 - z2) * ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1))) / a012 / l12;
float lc = -((x1 - x2) * ((x0 - x1) * (z0 - z2) - (x0 - x2) * (z0 - z1)) + (y1 - y2) * ((y0 - y1) * (z0 - z2) - (y0 - y2) * (z0 - z1))) / a012 / l12;
//ld2为点到直线的距离
float ld2 = a012 / l12;
//这里的s是个权重, 表示s在这个least-square问题中的置信度, 每个点的置信度不一样
//理论上, 这个权重, 与点到面距离负相关, 距离越大, 置信度越低, 这里相当于是一个在loss之外加了一个鲁棒性函数, 用来过减弱离群值的影响
//源代码中只是简单的用1-距离表示权重
//你可以设计自己的鲁棒性函数来替代这一行代码
float s = 1 - 0.9 * fabs(ld2);
if (s > 0.1)
{
//复用PointType传递偏导数, (la, lb, lc)是点到直线的垂线对应的向量, 也是点线距离相对与点坐标的偏导, 详见文章的公式推导部分.
//ld2是loss
PointType coeff;
coeff.x = s * la;
coeff.y = s * lb;
coeff.z = s * lc;
coeff.intensity = s * ld2;
points_selected.push_back(corner_feature_points[i]);
}
else
{
//距离无效, 本点匹配失败, 此点不对后续的优化贡献约束
}
}
}
}
void LaMapping::newLaserProc(pcl::PointCloud<PointType>::Ptr laser)
{
frame_count_++;
//第一帧, 完成初始化工作
if(frame_count_ == 1)
{
//记录IMU odom(也可以用其他形式的odometry)
prepareForNextFrame();
//第一帧根据当前pose转换到map坐标系下, 作为初始地图
updateFeatureMaps();
//地图生成kdtree, 便于后续查找
updateKdTrees();
return;
}
//每隔几帧处理一次
if (frame_count_ % 5 == 0)
{
//根据odometry进行位姿的predict
predictTransformByOdom();
//迭代优化位姿
doOptimize();
//迭代结束更新相关的转移矩阵
prepareForNextFrame();
//局部地图都要更新
updateFeatureMaps();
//地图生成kdtree, 便于后续查找
updateKdTrees();
}
}#include <cmath>
#include <string>
#include <Eigen/Core>
#include <Eigen/Geometry>
void matrixToEulerYXZ(Eigen::Matrix3d& m, Eigen::Vector3d &out)
{
//对照WIKIPEDIA的表运算(YXZ外旋)
double z = atan2(m(1,0), m(1,1));
double cos_x = m(1,1) / cos(z);
double x = atan2(-m(1,2), cos_x);
double y = atan2(m(0,2), m(2,2));
out[0] = x;
out[1] = y;
out[2] = z;
}
void matrixToRtYXZ(Eigen::Matrix4d& matrix, Eigen::Vector3d &euler_r, Eigen::Vector3d &euler_t)
{
Eigen::Matrix3d matrix_r = matrix.block(0,0,3,3);
euler_t[0] = matrix(0,3);
euler_t[1] = matrix(1,3);
euler_t[2] = matrix(2,3);
matrixToEulerYXZ(matrix_r, euler_r);
}
void eulerToMatrixYXZ(Eigen::Matrix3d& m, Eigen::Vector3d &euler)
{
m = Eigen::AngleAxisd(euler[1], Eigen::Vector3d::UnitY()) * Eigen::AngleAxisd(euler[0], Eigen::Vector3d::UnitX()) * Eigen::AngleAxisd(euler[2], Eigen::Vector3d::UnitZ());
}
void rtToMatrixYXZ(Eigen::Vector3d &r, Eigen::Vector3d &t, Eigen::Matrix4d& m)
{
Eigen::Matrix3d m_r;
eulerToMatrixYXZ(m_r, r);
m.block(0,0,3,3) = m_r;
m(0,3) = t[0];
m(1,3) = t[1];
m(2,3) = t[2];
m(3, 0) = 0;
m(3, 1) = 0;
m(3, 2) = 0;
m(3, 3) = 1;
}
//全局变量
//前一帧的ODOM pose, r是欧拉角,t是平移向量, 请自行维护
Eigen::Vector3d odometry_pre_r_;
Eigen::Vector3d odometry_pre_t_;
//当前的ODOM pose, r是欧拉角,t是平移向量, 请自行维护
Eigen::Vector3d odometry_r_;
Eigen::Vector3d odometry_t_;
//前一帧的pose, r是欧拉角,t是平移向量, 请自行维护
Eigen::Vector3d pose_pre_r_;
Eigen::Vector3d pose_pre_r_;
//基于predict得到transformToOptimize_, 作为优化的初始值
void predictTransformByOdom(Eigen::Vector3d &dst_r, Eigen::Vector3d &dst_t)
{
Eigen::Matrix4d odom_m1, odom_m2, odom_trans;
//LOAM中的变换都是欧拉角表示, YXZ顺序外旋的欧拉角
//将前一帧的ODOM(R, T)转换为4*4变换矩阵形式
rtToMatrixYXZ(odometry_pre_r_, odometry_pre_t_, odom_m1);
//将当前帧的ODOM(R, T)转换为4*4变换矩阵形式
rtToMatrixYXZ(odometry_r_, odometry_t_, odom_m2);
//求两帧之间的变换矩阵, 当前帧变换到前一帧
//W1 * 12 = W2 ->12 = W1逆*W2
odom_trans = odom_m1.inverse()*odom_m2;
//将前一帧的pose(R,T)转换为4*4变换矩阵形式
Eigen::Matrix4d pose;
rtToMatrixYXZ(pose_pre_r_, pose_pre_t_, pose);
//将ODOM得到的变换矩阵作用于前一帧POSE得到当前帧的POSE估计
//W2 = W1*12
pose = pose*odom_trans;
//4*4矩阵格式的POSE转换为(R,T)格式的POSE
matrixToRtYXZ(pose, dst_r, dst_t);
//now,dst_r, dst_t就是我们预测后的pose
}