diff --git a/README.md b/README.md
index 200056a..79a7419 100644
--- a/README.md
+++ b/README.md
@@ -1,8 +1,7 @@
 -F-1 Method
-==========
+# F-1 Method
-F-1 Method
-==========
+# F-1 Method
@@ -34,24 +33,40 @@ F-1 Method
-This package implements the F-1 method descibed in Pasquier et al. (2019).
-It allows for efficient quasi-auto-differentiation of an objective function defined implicitly by the solution of a steady-state problem represented by a discretized system of nonlinear partial differential equations that takes the form
+This package implements the F-1 method described in Pasquier et al. (in preparation).
+It allows for efficient quasi-auto-differentiation of an objective function defined implicitly by the solution of a steady-state problem.
-&space;=&space;0) +Consider a discretized system of nonlinear partial differential equations that takes the form
-where
-
+Consider a discretized system of nonlinear partial differential equations that takes the form
-where
- -is a column vector of the model state variables and
-
-is a column vector of the model state variables and
-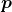 -is a vector of parameters.
-Specifically, the F-1 method allows for an efficient computation of both the gradient vector and the Hessian matrix of a generic objective function defined by
-
-is a vector of parameters.
-Specifically, the F-1 method allows for an efficient computation of both the gradient vector and the Hessian matrix of a generic objective function defined by
-&space;\equiv&space;f(\boldsymbol{s},\boldsymbol{p})) -where
-
-where
-) -is the steady-state solution of the system, i.e., such that
-
-is the steady-state solution of the system, i.e., such that
-&space;=&space;0) .
+```
+F(x,p) = 0
+```
+
+where `x` is a column vector of the model state variables and `p` is a vector of parameters.
+The F-1 method then allows for an efficient computation of both the gradient vector and the Hessian matrix of a generic objective function defined by
+
+```
+objective(p) = f(s(p),p)
+```
+
+where `s(p)` is the steady-state solution of the system, i.e., such that `F(s(p),p) = 0` and where `f(x,p)` is for example a measure of the mismatch between observed state, parameters, and observations.
+Optimizing the model is then simply done by minimizing `objective(p)`.
+(See Pasquier et al., in prep., for more details.)
+
+## Advantages of the F-1 method
+
+The F-1 method is **easy** to use, gives **accurate** results, and is computationally **fast**:
+
+- **Easy** — The F-1 method basically just needs the user to provide a solver (for finding the steady-state), the mismatch function, `f`, the state function, `F`, and their derivatives, `∇ₓf` and `∇ₓF` w.r.t. the state `x`.
+ (Note these derivatives can be computed numerically, via the [ForwardDiff](https://github.com/JuliaDiff/ForwardDiff.jl) package for example.)
+- **Accurate** — Thanks to dual and hyperdual numbers, the accuracy of the gradient and Hessian, as computed by the F-1 method, are close to machine precision.
+ (The F-1 method uses the [DualNumbers](https://github.com/JuliaDiff/DualNumbers.jl) and [HyperDualNumbers](https://github.com/JuliaDiff/HyperDualNumbers.jl) packages.)
+- **Fast** — The F-1 method is as fast as if you derived and an analytical formulas for every first and second derivatives in *and* used those in the most efficient way.
+ This is because the bottleneck of such computations is the number of matrix factorizations, and the F-1 method only requires a single one (compared to standard autodifferentiation methods that take the steady-state solver as a black box).
+
+## What's needed?
-A requirement of the F-1 method is that the Jacobian matrix
.
+```
+F(x,p) = 0
+```
+
+where `x` is a column vector of the model state variables and `p` is a vector of parameters.
+The F-1 method then allows for an efficient computation of both the gradient vector and the Hessian matrix of a generic objective function defined by
+
+```
+objective(p) = f(s(p),p)
+```
+
+where `s(p)` is the steady-state solution of the system, i.e., such that `F(s(p),p) = 0` and where `f(x,p)` is for example a measure of the mismatch between observed state, parameters, and observations.
+Optimizing the model is then simply done by minimizing `objective(p)`.
+(See Pasquier et al., in prep., for more details.)
+
+## Advantages of the F-1 method
+
+The F-1 method is **easy** to use, gives **accurate** results, and is computationally **fast**:
+
+- **Easy** — The F-1 method basically just needs the user to provide a solver (for finding the steady-state), the mismatch function, `f`, the state function, `F`, and their derivatives, `∇ₓf` and `∇ₓF` w.r.t. the state `x`.
+ (Note these derivatives can be computed numerically, via the [ForwardDiff](https://github.com/JuliaDiff/ForwardDiff.jl) package for example.)
+- **Accurate** — Thanks to dual and hyperdual numbers, the accuracy of the gradient and Hessian, as computed by the F-1 method, are close to machine precision.
+ (The F-1 method uses the [DualNumbers](https://github.com/JuliaDiff/DualNumbers.jl) and [HyperDualNumbers](https://github.com/JuliaDiff/HyperDualNumbers.jl) packages.)
+- **Fast** — The F-1 method is as fast as if you derived and an analytical formulas for every first and second derivatives in *and* used those in the most efficient way.
+ This is because the bottleneck of such computations is the number of matrix factorizations, and the F-1 method only requires a single one (compared to standard autodifferentiation methods that take the steady-state solver as a black box).
+
+## What's needed?
-A requirement of the F-1 method is that the Jacobian matrix ) can be created, stored, and factorized.
+A requirement of the F-1 method is that the Jacobian matrix `A = ∇ₓf` can be created, stored, and factorized.
To use the F-1 method, the user must:
@@ -59,26 +74,44 @@ To use the F-1 method, the user must:
- overload the `solve` function and the `SteadyStateProblem` constructor from [DiffEqBase](https://github.com/JuliaDiffEq/DiffEqBase.jl). (An example is given in the CI tests — see, e.g., the [`test/simple_setup.jl`](test/simple_setup.jl) file.)
- Provide the derivatives of `f` and `F` with respect to the state, `x`.
-### Simple usage
+## A concrete example
-Make sure you have olverloaded `solve` from DiffEqBase.
-Once an initial state, `x₀`, and some parameters, `p₀`, are chosen, simply evaluate the derivatives with
+Make sure you have olverloaded `solve` from DiffEqBase
+(an example of how to do this is given in the [documentation](https://briochemc.github.io/F1Method.jl/stable/)).
+Once initial values for the state, `x₀`, and parameters, `p₀`, are chosen, simply initialize the required memory cache, `mem` via
```julia
# Initialize the cache for storing reusable objects
mem = F1Method.initialize_mem(x₀, p₀)
+```
+
+wrap the functions into functions of `p` only via
+
+```julia
# Wrap the objective, gradient, and Hessian functions
objective(p) = F1Method.f̂(f, F, ∇ₓF, mem, p, myAlg(); my_options...)
-gradient(p) = F1Method.∇f̂(f, F, ∇ₓf, ∇ₓF, mem, p₀, myAlg(); my_options...)
-hessian(p) = F1Method.∇²f̂(f, F, ∇ₓf, ∇ₓF, mem, p₀, myAlg(); my_options...)
+gradient(p) = F1Method.∇f̂(f, F, ∇ₓf, ∇ₓF, mem, p, myAlg(); my_options...)
+hessian(p) = F1Method.∇²f̂(f, F, ∇ₓf, ∇ₓF, mem, p, myAlg(); my_options...)
+```
-# Compute the objective function, 𝑓̂(𝒑)
+and compute the objective, gradient, or Hessian via either of
+
+```julia
objective(p₀)
-# Compute the gradient, ∇𝑓̂(𝒑)
gradient(p₀)
-# Compute the Hessian matrix, ∇²𝑓̂(𝒑)
hessian(p₀)
```
+
+That's it.
+You were told it was simple, weren't you?
+Now you can test how fast and accurate it is!
+(Or trust our published work, Pasquier et al., in prep.)
+
+## Citing the software
+
+If you use this package, or implement your own package based on the F-1 method please cite us.
+If you use the F-1 method, please cite our Pasquier et al. (in prep.) publication.
+If you also use this package directly, please cite us using the [CITATION.bib](./CITATION.bib), which contains a bibtex entry for the software.
can be created, stored, and factorized.
+A requirement of the F-1 method is that the Jacobian matrix `A = ∇ₓf` can be created, stored, and factorized.
To use the F-1 method, the user must:
@@ -59,26 +74,44 @@ To use the F-1 method, the user must:
- overload the `solve` function and the `SteadyStateProblem` constructor from [DiffEqBase](https://github.com/JuliaDiffEq/DiffEqBase.jl). (An example is given in the CI tests — see, e.g., the [`test/simple_setup.jl`](test/simple_setup.jl) file.)
- Provide the derivatives of `f` and `F` with respect to the state, `x`.
-### Simple usage
+## A concrete example
-Make sure you have olverloaded `solve` from DiffEqBase.
-Once an initial state, `x₀`, and some parameters, `p₀`, are chosen, simply evaluate the derivatives with
+Make sure you have olverloaded `solve` from DiffEqBase
+(an example of how to do this is given in the [documentation](https://briochemc.github.io/F1Method.jl/stable/)).
+Once initial values for the state, `x₀`, and parameters, `p₀`, are chosen, simply initialize the required memory cache, `mem` via
```julia
# Initialize the cache for storing reusable objects
mem = F1Method.initialize_mem(x₀, p₀)
+```
+
+wrap the functions into functions of `p` only via
+
+```julia
# Wrap the objective, gradient, and Hessian functions
objective(p) = F1Method.f̂(f, F, ∇ₓF, mem, p, myAlg(); my_options...)
-gradient(p) = F1Method.∇f̂(f, F, ∇ₓf, ∇ₓF, mem, p₀, myAlg(); my_options...)
-hessian(p) = F1Method.∇²f̂(f, F, ∇ₓf, ∇ₓF, mem, p₀, myAlg(); my_options...)
+gradient(p) = F1Method.∇f̂(f, F, ∇ₓf, ∇ₓF, mem, p, myAlg(); my_options...)
+hessian(p) = F1Method.∇²f̂(f, F, ∇ₓf, ∇ₓF, mem, p, myAlg(); my_options...)
+```
-# Compute the objective function, 𝑓̂(𝒑)
+and compute the objective, gradient, or Hessian via either of
+
+```julia
objective(p₀)
-# Compute the gradient, ∇𝑓̂(𝒑)
gradient(p₀)
-# Compute the Hessian matrix, ∇²𝑓̂(𝒑)
hessian(p₀)
```
+
+That's it.
+You were told it was simple, weren't you?
+Now you can test how fast and accurate it is!
+(Or trust our published work, Pasquier et al., in prep.)
+
+## Citing the software
+
+If you use this package, or implement your own package based on the F-1 method please cite us.
+If you use the F-1 method, please cite our Pasquier et al. (in prep.) publication.
+If you also use this package directly, please cite us using the [CITATION.bib](./CITATION.bib), which contains a bibtex entry for the software.
 -F-1 Method
-==========
+# F-1 Method
-F-1 Method
-==========
+# F-1 Method