The goal is to take a set of coils and optimize them to produce a magnetic field with precise quasiaxisymmetry. This is done by computing magnetic surfaces in the vacuum field. Then, the field's deviation from quasisymmetry on that surface is determined and used in the formulation of an optimization problem. With an adjoint approach, we are able to obtain analytic derivatives for this optimization problem, yielding an efficient gradient-based algorithm. Starting from an initial coil set that presents nested magnetic surfaces for a large fraction of the volume, our method converges rapidly to coil systems generating fields with excellent quasi-symmetry and low particle losses.
![QA-III[24] coils](https://raw.githubusercontent.com/andrewgiuliani/PySurfaceOpt/main/len24.png)
To use this code, first clone the repository including all its submodules, via
git clone --recursive
and then install SIMSOPT via
pip install -e simsopt/
Refer to the SIMSOPT installation instructions here if you have any trouble installing it. Finally, install PySurfaceOpt using
pip install -e .
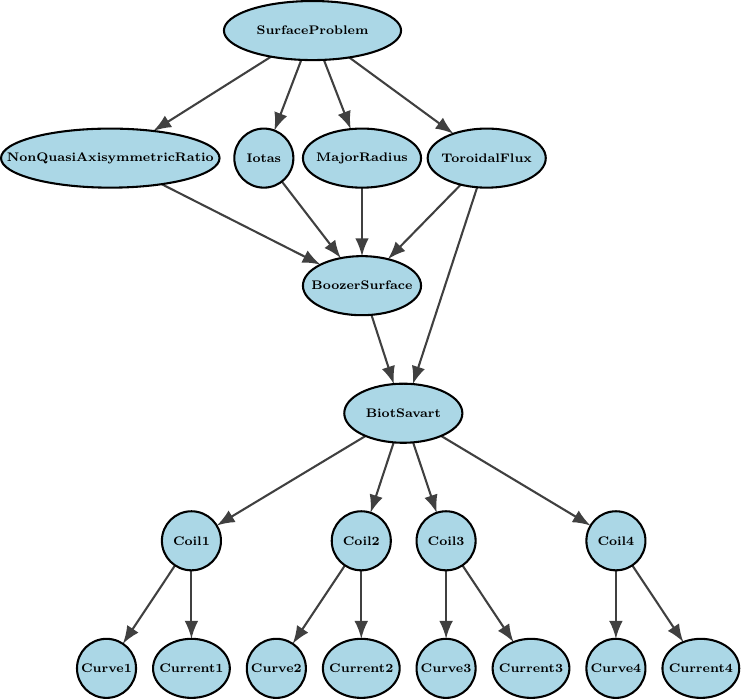
The different penalty terms of the optimization problem are implemented using the optimizable framework in SIMSOPT for efficient caching. The dependencies between the various quantities result in a graph that can be used for caching, i.e., penalty terms are only recomputed when quantities that they depend on are changed. For example, the toroidal flux penalty term depends both on the geometry of the computed Boozer surface and the magnetic field computed via the Biot Savart law. We show a simplified dependency graph of the quantities used to optimize for quasiaxisymmetry in the below figure to illustrate how this works for a single Boozer surface computed from the magnetic field generated by four coils and four currents. The full optimization problem solved the included examples result in much more complex dependency graphs.
