- An image pyramid is a collection of images - all arising from a single original image - that are successively downsampled until some desired stopping point is reached.
- Used to downsample images
- Representing image in multiple scales
- They are called pyramids because the processed image can be represented in form of pyramids of different size(2^n+1)
It works on Aliasing "Aliasing is an effect that causes different signals to become indistinguishable ".
Image I of size (2N+1)x(2N+1) Output: Images g
The whole pyramid is only 4/3 the size of the original image.
#### To generate a Gaussian pyramid, iterate between these two steps: * Smoothing: Remove high-frequency components that could cause aliasing.
Smoothing can be achieved by averaging neighboring pixels. The strength of a smoothing operator is proportional to the number of pixels it averages. Averaging can be computed as the Cross-Correlation of the image with a constant kernel, Cross correlation in 1D can be computed using Matrix multiplication
- Down-sampling: Reduce the image size by ½ at each level.
- To make smoothed copies of images at different scales.
- highly redundant, coarse scales provide much of the information in the finer scales
- Scale invariant template matching (like faces)
- Progressive image transmission
- Image blending
- Used for multi-scale edge estimation
- Efficient feature search
Some Good example of image blending
https://docs.opencv.org/3.4/d4/d1f/tutorial_pyramids.html
http://www.cs.toronto.edu/~jepson/csc320/notes/pyramids.pdf
https://inst.eecs.berkeley.edu/~cs194-26/fa17/Lectures/FilteringGaussianPyramids.pdf
https://www.youtube.com/watch?v=1YjC9sTm0vM
https://www.youtube.com/watch?v=8yvln2atFkA
Laplacian Pyramids are formed from the Gaussian Pyramids. There is no exclusive function for that. Laplacian pyramid images are like edge images only. Most of its elements are zeros. They are used in image compression. A level in Laplacian Pyramid is formed by the difference between that level in Gaussian Pyramid and expanded version of its upper level in Gaussian Pyramid.
- Used to reconstruct an upsampled image from an image lower in the pyramid (with less resolution)
- The Laplacian pyramid provides a coarse representation of the image as well as a set of detail images (bandpass components) at different scales.
Over-complete decomposition based on difference-of-lowpass filters; the image is recursively decomposed into low-pass and highpass bands.
- Each band of the Laplacian pyramid is the difference between two
adjacent low-pass images of the Gaussian pyramid,
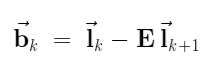

- Eliminates blocking artifacts of JPEG at low frequencies because of the overlapping basis functions.
- approach also allows for progressive transmission, since low-pass representations are reasonable approximations to the image.
- coding and image reconstruction are simple
- A Laplacian filter is an edge detector used to compute the second derivatives of an image, measuring the rate at which the first derivatives change.
- Laplacian operator is to restore fine detail to an image which has been smoothed to remove noise.
- Applies a Laplacian operator to the grayscale image and stores the output image.
https://docs.opencv.org/3.4/d4/d1f/tutorial_pyramids.html
http://www.cs.toronto.edu/~jepson/csc320/notes/pyramids.pdf
https://inst.eecs.berkeley.edu/~cs194-26/fa17/Lectures/FilteringGaussianPyramids.pdf
https://www.youtube.com/watch?v=aDY4aBLFOIg
https://www.youtube.com/watch?v=_wZeX_35Iew
- In Image Blending





