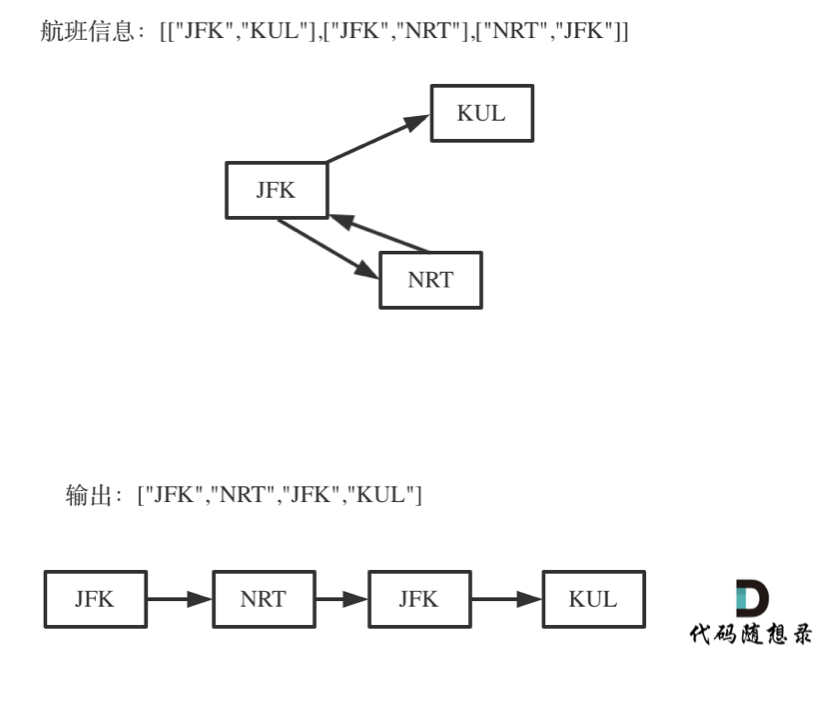
这也可以用回溯法? 其实深搜和回溯也是相辅相成的,毕竟都用递归。
题目地址:https://leetcode-cn.com/problems/reconstruct-itinerary/
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
提示:
- 如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前
- 所有的机场都用三个大写字母表示(机场代码)。
- 假定所有机票至少存在一种合理的行程。
- 所有的机票必须都用一次 且 只能用一次。
示例 1: 输入:[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]] 输出:["JFK", "MUC", "LHR", "SFO", "SJC"]
示例 2: 输入:[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]] 输出:["JFK","ATL","JFK","SFO","ATL","SFO"] 解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
这道题目还是很难的,之前我们用回溯法解决了如下问题:组合问题,分割问题,子集问题,排列问题。
直觉上来看 这道题和回溯法没有什么关系,更像是图论中的深度优先搜索。
实际上确实是深搜,但这是深搜中使用了回溯的例子,在查找路径的时候,如果不回溯,怎么能查到目标路径呢。
所以我倾向于说本题应该使用回溯法,那么我也用回溯法的思路来讲解本题,其实深搜一般都使用了回溯法的思路,在图论系列中我会再详细讲解深搜。
这里就是先给大家拓展一下,原来回溯法还可以这么玩!
这道题目有几个难点:
- 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
- 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
- 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
- 搜索的过程中,如何遍历一个机场所对应的所有机场。
针对以上问题我来逐一解答!
对于死循环,我来举一个有重复机场的例子:
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,如果在解题的过程中没有对集合元素处理好,就会死循环。
有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
一个机场映射多个机场,机场之间要靠字母序排列,一个机场映射多个机场,可以使用std::unordered_map,如果让多个机场之间再有顺序的话,就是用std::map 或者std::multimap 或者 std::multiset。
如果对map 和 set 的实现机制不太了解,也不清楚为什么 map、multimap就是有序的同学,可以看这篇文章关于哈希表,你该了解这些!。
这样存放映射关系可以定义为 unordered_map<string, multiset<string>> targets 或者 unordered_map<string, map<string, int>> targets。
含义如下:
unordered_map<string, multiset<string>> targets:unordered_map<出发机场, 到达机场的集合> targets
unordered_map<string, map<string, int>> targets:unordered_map<出发机场, map<到达机场, 航班次数>> targets
这两个结构,我选择了后者,因为如果使用unordered_map<string, multiset<string>> targets 遍历multiset的时候,不能删除元素,一旦删除元素,迭代器就失效了。
再说一下为什么一定要增删元素呢,正如开篇我给出的图中所示,出发机场和到达机场是会重复的,搜索的过程没及时删除目的机场就会死循环。
所以搜索的过程中就是要不断的删multiset里的元素,那么推荐使用unordered_map<string, map<string, int>> targets。
在遍历 unordered_map<出发机场, map<到达机场, 航班次数>> targets的过程中,可以使用"航班次数"这个字段的数字做相应的增减,来标记到达机场是否使用过了。
如果“航班次数”大于零,说明目的地还可以飞,如果如果“航班次数”等于零说明目的地不能飞了,而不用对集合做删除元素或者增加元素的操作。
相当于说我不删,我就做一个标记!
这道题目我使用回溯法,那么下面按照我总结的回溯模板来:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
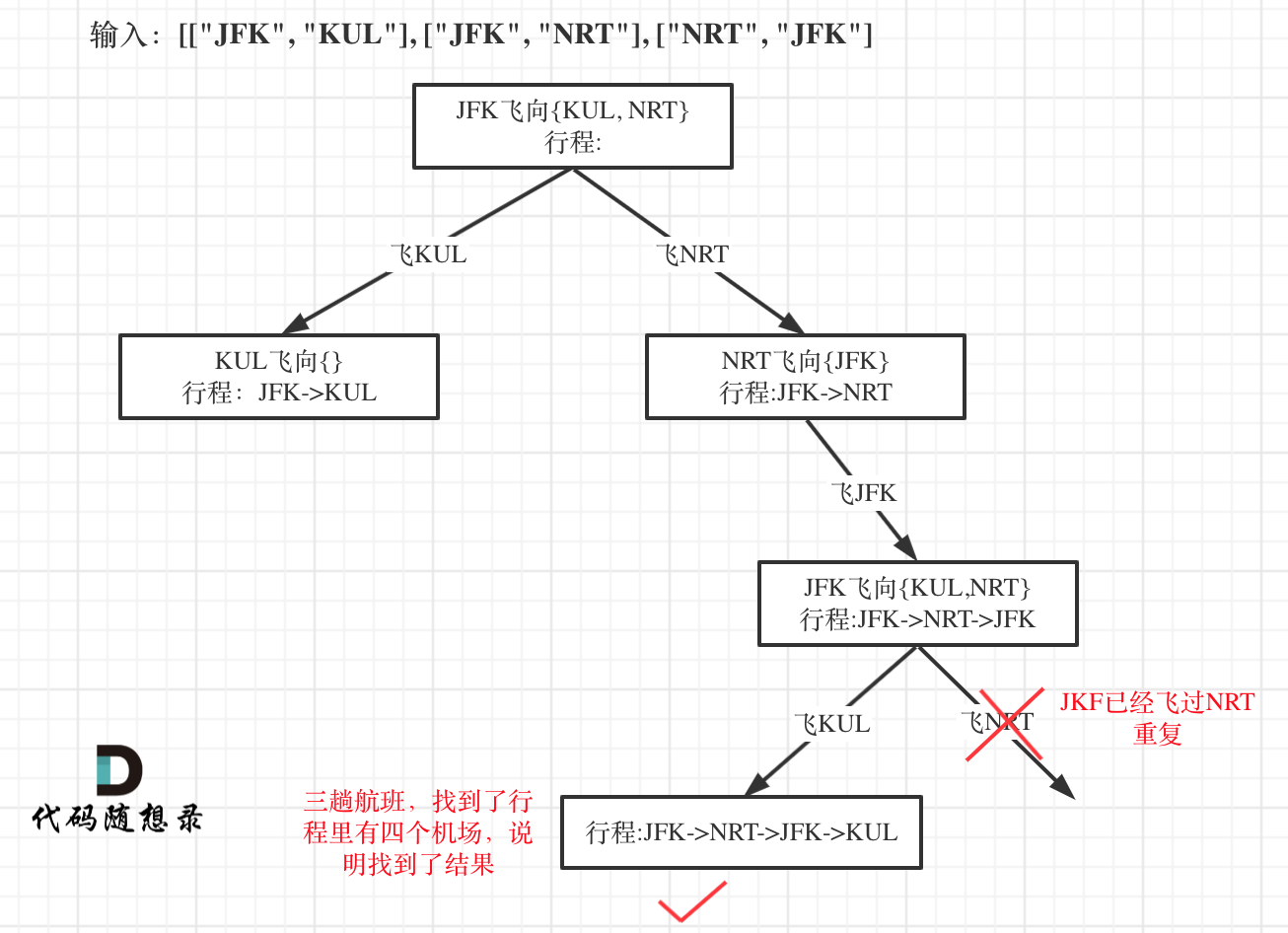
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
开始回溯三部曲讲解:
- 递归函数参数
在讲解映射关系的时候,已经讲过了,使用unordered_map<string, map<string, int>> targets; 来记录航班的映射关系,我定义为全局变量。
当然把参数放进函数里传进去也是可以的,我是尽量控制函数里参数的长度。
参数里还需要ticketNum,表示有多少个航班(终止条件会用上)。
代码如下:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {
注意函数返回值我用的是bool!
我们之前讲解回溯算法的时候,一般函数返回值都是void,这次为什么是bool呢?
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?详细介绍过。
当然本题的targets和result都需要初始化,代码如下:
for (const vector<string>& vec : tickets) {
targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场
- 递归终止条件
拿题目中的示例为例,输入: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]] ,这是有4个航班,那么只要找出一种行程,行程里的机场个数是5就可以了。
所以终止条件是:我们回溯遍历的过程中,遇到的机场个数,如果达到了(航班数量+1),那么我们就找到了一个行程,把所有航班串在一起了。
代码如下:
if (result.size() == ticketNum + 1) {
return true;
}
已经看习惯回溯法代码的同学,到叶子节点了习惯性的想要收集结果,但发现并不需要,本题的result相当于 回溯算法:求组合总和!中的path,也就是本题的result就是记录路径的(就一条),在如下单层搜索的逻辑中result就添加元素了。
- 单层搜索的逻辑
回溯的过程中,如何遍历一个机场所对应的所有机场呢?
这里刚刚说过,在选择映射函数的时候,不能选择unordered_map<string, multiset<string>> targets, 因为一旦有元素增删multiset的迭代器就会失效,当然可能有牛逼的容器删除元素迭代器不会失效,这里就不在讨论了。
可以说本题既要找到一个对数据进行排序的容器,而且还要容易增删元素,迭代器还不能失效。
所以我选择了unordered_map<string, map<string, int>> targets 来做机场之间的映射。
遍历过程如下:
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}可以看出 通过unordered_map<string, map<string, int>> targets里的int字段来判断 这个集合里的机场是否使用过,这样避免了直接去删元素。
分析完毕,此时完整C++代码如下:
class Solution {
private:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {
if (result.size() == ticketNum + 1) {
return true;
}
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}
return false;
}
public:
vector<string> findItinerary(vector<vector<string>>& tickets) {
targets.clear();
vector<string> result;
for (const vector<string>& vec : tickets) {
targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场
backtracking(tickets.size(), result);
return result;
}
};一波分析之后,可以看出我就是按照回溯算法的模板来的。
代码中
for (pair<const string, int>& target : targets[result[result.size() - 1]])
pair里要有const,因为map中的key是不可修改的,所以是pair<const string, int>。
如果不加const,也可以复制一份pair,例如这么写:
for (pair<string, int>target : targets[result[result.size() - 1]])
本题其实可以算是一道hard的题目了,关于本题的难点我在文中已经列出了。
如果单纯的回溯搜索(深搜)并不难,难还难在容器的选择和使用上。
本题其实是一道深度优先搜索的题目,但是我完全使用回溯法的思路来讲解这道题题目,算是给大家拓展一下思维方式,其实深搜和回溯也是分不开的,毕竟最终都是用递归。
如果最终代码,发现照着回溯法模板画的话好像也能画出来,但难就难如何知道可以使用回溯,以及如果套进去,所以我再写了这么长的一篇来详细讲解。
就酱,很多录友表示和「代码随想录」相见恨晚,那么帮Carl宣传一波吧,让更多同学知道这里!
python:
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
# defaultdic(list) 是为了方便直接append
tickets_dict = defaultdict(list)
for item in tickets:
tickets_dict[item[0]].append(item[1])
'''
tickets_dict里面的内容是这样的
{'JFK': ['SFO', 'ATL'], 'SFO': ['ATL'], 'ATL': ['JFK', 'SFO']})
'''
path = ["JFK"]
def backtracking(start_point):
# 终止条件
if len(path) == len(tickets) + 1:
return True
tickets_dict[start_point].sort()
for _ in tickets_dict[start_point]:
#必须及时删除,避免出现死循环
end_point = tickets_dict[start_point].pop(0)
path.append(end_point)
# 只要找到一个就可以返回了
if backtracking(end_point):
return True
path.pop()
tickets_dict[start_point].append(end_point)
backtracking("JFK")
return pathC语言版本:
char **result;
bool *used;
int g_found;
int cmp(const void *str1, const void *str2)
{
const char **tmp1 = *(char**)str1;
const char **tmp2 = *(char**)str2;
int ret = strcmp(tmp1[0], tmp2[0]);
if (ret == 0) {
return strcmp(tmp1[1], tmp2[1]);
}
return ret;
}
void backtracting(char *** tickets, int ticketsSize, int* returnSize, char *start, char **result, bool *used)
{
if (*returnSize == ticketsSize + 1) {
g_found = 1;
return;
}
for (int i = 0; i < ticketsSize; i++) {
if ((used[i] == false) && (strcmp(start, tickets[i][0]) == 0)) {
result[*returnSize] = (char*)malloc(sizeof(char) * 4);
memcpy(result[*returnSize], tickets[i][1], sizeof(char) * 4);
(*returnSize)++;
used[i] = true;
/*if ((*returnSize) == ticketsSize + 1) {
return;
}*/
backtracting(tickets, ticketsSize, returnSize, tickets[i][1], result, used);
if (g_found) {
return;
}
(*returnSize)--;
used[i] = false;
}
}
return;
}
char ** findItinerary(char *** tickets, int ticketsSize, int* ticketsColSize, int* returnSize){
if (tickets == NULL || ticketsSize <= 0) {
return NULL;
}
result = malloc(sizeof(char*) * (ticketsSize + 1));
used = malloc(sizeof(bool) * ticketsSize);
memset(used, false, sizeof(bool) * ticketsSize);
result[0] = malloc(sizeof(char) * 4);
memcpy(result[0], "JFK", sizeof(char) * 4);
g_found = 0;
*returnSize = 1;
qsort(tickets, ticketsSize, sizeof(tickets[0]), cmp);
backtracting(tickets, ticketsSize, returnSize, "JFK", result, used);
*returnSize = ticketsSize + 1;
return result;
}java 版本:
class Solution {
private Deque<String> res;
private Map<String, Map<String, Integer>> map;
private boolean backTracking(int ticketNum){
if(res.size() == ticketNum + 1){
return true;
}
String last = res.getLast();
if(map.containsKey(last)){//防止出现null
for(Map.Entry<String, Integer> target : map.get(last).entrySet()){
int count = target.getValue();
if(count > 0){
res.add(target.getKey());
target.setValue(count - 1);
if(backTracking(ticketNum)) return true;
res.removeLast();
target.setValue(count);
}
}
}
return false;
}
public List<String> findItinerary(List<List<String>> tickets) {
map = new HashMap<String, Map<String, Integer>>();
res = new LinkedList<>();
for(List<String> t : tickets){
Map<String, Integer> temp;
if(map.containsKey(t.get(0))){
temp = map.get(t.get(0));
temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
}else{
temp = new TreeMap<>();//升序Map
temp.put(t.get(1), 1);
}
map.put(t.get(0), temp);
}
res.add("JFK");
backTracking(tickets.size());
return new ArrayList<>(res);
}
}