Table of contents:

• Best Time to Buy And Sell Stock
• Maximum Sum of Subarray
• Trace and Normal of Matrix
• Sort an Array of 0s, 1s and 2s
• Prefix Sum
• First Negative Integer In Every K size Window
• Peak In 1D Array

Best Time to Buy And Sell Stock

The problem states that there is an array or vector that contains N elements and elements stores stocks price at that day.
For example:
Let the array be [7,1,5,3,6,4]
Then i=0 stores stocks price at 1st day that is 7.

• Then part of the problem states that you can not sell before buying and that means we can not sell at i=0 and buy at i=1 for profit of 6.
• The next part of the problem is if it can not have a profit then return 0 meaning if no profit don't buy anything
• example:

           Input :[7,1] 
           Output: 0

Algorithm

• 1^st initiate the buying price as INT_MAX as we want to minimize it in later steps. Let us say buying price be b
• 2^nd initiate the maximum profit as 0 as it is given in the problem to return 0 if in case of no profit. Let us say maximum profit be p.
• 3^rd Now iterate over the array or vector if current element at i is smaller then the previous element then update b to that element.
• 4^th Check wether the differece of current b with the current element is lager than previous value then update the p value to the value of differnce.
• 5^th continue 3^rd and 4^th step till the lenth of the array or vector.

Complexity

Time complexity: O(n) 
Space complexity: O(1) 

Maximum Sum of Subarray:

• Maximum Sum Subarray
• Example
• Different Approches
  • Brute force Approach (simple)
  • Cumulative Sum Approach
  • Efficient Approach: Kadane’s Algorithm

Maximum Sum Subarray:

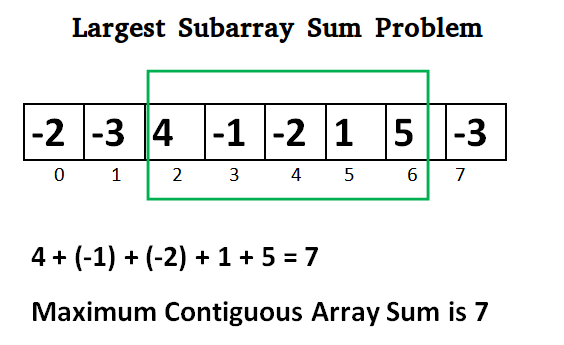
Given an array of integers, the task is to find the maximum subarray sum possible of all the non-empty subarrays.

Example:

Sr. No.	Input	Output	Explanation
1	[-3, -4, 5, -1, 2, -4, 6, -1]	8	The subarray [5, -1, 2, -4, 6] has the maximum sum among all subarrays with sum 8.
2	[-2, 3, -1, 2]	4	The subarray [3, -1, 2] has the maximum sum among all subarrays with sum 4.
3	[-5, 8, 9, -6, 10, -15, 3]	21	The subarray [8, 9, -6, 10] has the maximum sum among all subarrays with sum 21.
4	[-4, -7, -1, 5,-2]	4	The subarray [-1, 5] has the maximum sum among all subarrays with sum 4.

Different Approches:

We would be solving the problem by following approaches –

1. Brute force approach
2. Cumulative sum approach
3. Efficient Approach: Kadane’s Algorithm

1. Brute force Approach (simple)

The simple approach to solve this problem is to run three for loops and For each subarray arr[i..j], calculate its sum. Update maxSum if last calculated sum is smaller than the current sum.

Algorithm:

int maxSubarraySum1 ( int a [] , int n) 
{ 
  int maxSum = INT_MIN
  for(i = 0 to n-1) 
  { 
    for(j = i to n-1) 
    { 
      int sum = 0 
      for(k = i to j) 
        sum = sum + a[k] 
      Update maxSum if its smaller than sum with the maxSum value 
    } 
  } 
return maxSum
}

Time Complexity: O(n^3), Where n is the size of the array.
Space Complexity: O(1)

2. Cumulative Sum Approach:

For each subarray arr[i..j], calculate its sum. Using prefix sum can reduce time to calculate the sum of arr[i..j] to O(1)

Algorithm:

int maxSubarraySum2 ( int a [] , int n) 
{ 
  int currsum[n+1]
  Currsum[0] = 0
  int maxSum = INT_MIN
  for(i = 1 to n-1) 
  { 
	  cumsum[i] = cumsum[i - 1] + a[i];
  }
  for(i = 1 to n-1) 
  { 
    int sum = 0 
    for(j = 0 to i) 
      sum = currsum[i - currsum[j] 
      Update maxSum if its smaller than sum with the maxSum value 
  } 
return maxSum
} 

Time Complexity: O(n^2), Where n is the size of the array.
Space Complexity: O(n)

3. Efficient Approach: Kadane’s Algorithm

Kadane’s Algorithm is an iterative dynamic programming algorithm. It calculates the maximum sum subarray ending at a particular position by using the maximum sum subarray ending at the previous position. Basic logic is to start taking the sum of the array, as soon as it gets negative, discard the current subarray, and start a new sum.

Algorithm:

Initialize:
  currsum = 0
  maxSum = INT_MIN
  
Loop for each element of the array
(a) currsum = currsum + a[i]
(b) if(currsum  < 0)
          currsum = 0
    Othewise maxSum = currsum
return max_so_far

Time complexity: O(n), Where n is the size of the array.
Space complexity: O(1)

Trace and Normal of Matrix

• Trace
• Normal
• Properties_of_trace_matrix
• Example
• Algorithim
• Time complexity

Trace:

The trace of a matrix A, defined by tr(A), is the sum of the diagonal elements of a matrix. Trace of a matrix is only possible for square matrix.

Normal:

The normal of matrix is the sum of all the elements of a matrix and then the square root of sum.

Properties of trace matrix:

 --> tr(A + B) = tr(A) +tr(B)
 --> tr(cA) = ctr(A)  ** c represents scalars
 --> tr(A) = tr(A^T)  ** T means transpose of matrix 

Example:

Trace:

we have taken following as the elements of a matrix 2 3 5 7 4 5 8 5 4

we have to add all the elements of the matrix and store it in sum variable,sum = 2+3+5+7+4+5+8+5+4 then we will find the square root of sum we get 6.55 so, normal of matrix = 6.55

Normal:

Now we will first check the conditions for trace of matrix (i.e. row==column) then we will add all the diagonal elements trace = 2+4+4 so, trace of matrix = 10

Algorithm:

1. Enter the order of a matrix (eg: 3X3 or 2X2 etc...)
2. Using loop enter the elements of a matrix .
3. Printing the elements of the matrix .
4. Finding the sum of all the elements of the matrix .
5. Then the square root of the sum using sqrt() to find the normal of the matrix and store it in variable normal.
6. Using the condition row == column we can find the sum of diagonal elements of a matrix , value of sum will be store in
 variable trace .
7. Print the value of normal and trace of a matrix .

Time complexity:

Time complexity of trace of a matrix is n^2.
Time complexity of normal of a matrix is n^2.

Sort an Array of 0s, 1s and 2s

- [1. Sort an Array of 0s, 1s and 2s](#1-sort-an-array-of-0s-1s-and-2s)
- [Dutch National Flag Algorithm](#dutch-national-flag-algorithm)
- [Properties](#properties)
- [Sample Output](#sample-output)

Sort an Array of 0s, 1s and 2s

Given an array consisting 0s, 1s and 2s. The task is to write a function that sorts the given array. The functions should put all 0s first, then all 1s and all 2s in last.

---

Dutch National Flag Algorithm

begin sortArray(array)
   int low = 0
   int mid = 0
   int high = array.size() - 1

   while(mid <= high)
      if (array[mid] == 0)
         swap(array[low], array[mid])
         low++
         mid++
      else if (array[mid] == 1)
         mid++
      else
         swap(array[mid], array[high])
         high--
      end if
   end while

   return array

end sortArray

Properties

• Time Complexity: O(n)
• Space Complexity: O(1)
• In-Place: Yes
• Stable: Yes

Sample Output

• For More Reference Please Check Out -> Geeks For Geeks

Prefix Sum

Given an array of N integers. Given Q queries and in each query given L and R print sum of array elements from index L to R (both inclusive)

Naive Approach

Use a loop to calculate the sum of numbers from l to r for each query.

Time Complexity: O(N) + O(Q*N) = 10^ 10
Space Complexity: O(1)

Optimial Approach

Use prefix sum , a pre-computation technique , to calculate the sum .

We declare a prefix[] array which stores the sum of numbers from 1 to ith index. prefix[i] ---> Stores the sum of numbers from 1 to ith index

So, to calculate the sum of numbers from l to r , we deduce a formula:

prefix[r] ----> Stores sum of numbers from 1 to rth index prefix[l-1] ----> Stores sum of numbers from 1 to (l-1)th index

So, to output the sum of numbers from l to r , we use this:
prefix[r]-prefix[l-1] (O(1) time complexity)

Time Complexity: O(N) + O(N) + O(Q) = 10^5 Space Complexity: O(N) + O(N) (Using prefix array)

First negative integer in every k size window:

• Example
• Approach Used
• Algorithm
• Time Complexity

First negative integer in every k size window:

Given an array and a positive integer k, find the first negative integer for each window(contiguous subarray) of size k. If a window does not contain a negative integer, then print 0 for that window. \

  Input : arr[] = {-8, 2, 3, -6, 10}, k = 2
  Output : -8 0 -6 -6
  First negative integer for each window of size k
  {-8, 2} = -8
  {2, 3} = 0 (does not contain a negative integer)
  {3, -6} = -6
  {-6, 10} = -6

  Input : arr[] = {12, -1, -7, 8, -15, 30, 16, 28} , k = 3
  Output : -1 -1 -7 -15 -15 0

Few Examples:

Sr. No.	Input	Output	Explanation
1	[-3, -4, 5, -1, 2, -4, 6] , 3	[-3, -4, -1, -1, -4]	[-3, -4, -1, -1, -4] are the first negative integer of every window of size 3.
2	[-2, 3, -1, 2] , 2	[-2, -1, -1]	[-2, -1, -1] are the first negative integer of every window of size 2.
3	[-5, 8, 9, -6, 10, -15, 3] , 3	[-5, -6 ,-6, -6, -15]	[-5, -6 ,-6, -6, -15] are the first negative integer of every window of size 3.
4	[-4, -7, 1, 5,2] , 2	[-4, -7, 0, 0]	[-4, -7, 0, 0] are the first negative integer of every window of size 2.

Approach Used -> Sliding Window Approach:

For every k size window store every element if negative in deque from rear end using for loop then check size of deque size if greater than 0 then then get the element from front and store it in vector. If deque size is 0 store 0 in vector. Move the window ahead if we have reached or passed the last element of the window.

Algorithm:

  1. Initialize deque and vector.
  2. Use loop for starting window that is till k.
  3. Push back the index in deque if element is negative.
  4. Push back 0 if element is positive.
  5. Check the size of deque after execution of loop if size > 0 get the front element of deque(index) store the element at that index in vector.
  6. Else store 0 in vector.
  7. Use loop from k till last index of array.
  8. Check if deque is not empty  && loop variable - front element of deque is not greater than or equal to k.
  9. If step 8 is true pop the front element in deque.
  10.Repeat  steps 5,6 and 8, 9  till execution of loop

Time and space complexity:

 Time Complexity =  O(n-k), Where n is the size of the array and k is window size.
 Space complexity = O(n-k+1), size of vector returned. 

Peak in 1D Array

• Introduction
• Examples
• Simple Approach
• Efficient Approach

Introduction

Peak element in 1D array is the element which is greater than or equal to its adjacent neighbours. For the first and last element in the array consider only one adjacent neighbour.

Examples

Example 1:

Example 2:

Example 3:

Simple Approach

Traverse the array linearly and check wheather the element is peak or not, by comparing with it's adjacent neighbours.

Algorithm

1. If size of the array is 1 then then return that element.
2. Checking for the corner cases:
   1. In the array if the first element is greater than or equal to second element then we return 0 (index of the first element).
   2. In the array if the last element is greater than or equal to second last element then we return n-1 (index of the last element).
3. Traverse the array from second element to second last element.
4. If the element is greater than or equal to both of it's adjacent neighbours then return the index of that element.

Code

int simplePeak(vector<int> &arr,int n){
  if(n==1) return 0
  if(arr[0]>=arr[1]) return 0
  if(arr[n-1]>=arr[n-2]) return n-1
  for(int i=1;i<n-1;i++){
      if(arr[i]>=arr[i+1] && arr[i]>=arr[i-1]) return i
  }
}

Time Complexity: O(n)
Auxillary Space: O(1)

Efficient Approach:

Algorithm

1. Make two variables,start=0 and end=n-1.
2. Iterate till start is less than end.
3. Check if the mid value is peak or not ,if yes then return mid.
4. If the element on the left side of mid element is more then update end=mid-1.
5. If the element on the right side of mid element is more then update start=mid+1.

Pseudo Code

begin efficientPeak(array,n)

     if(n == 1) return 0
     if(array[0] >= array[1]) return 0;
     if(array[n-1] >= array[n-2]) return n-1;

     int start = 0
     int mid = 0
     int end= n-1
 
     while(start <= end)
 	mid = (start + end)/2
 	if((array[mid] >= array[mid-1]) && (array[mid] >= array[mid+1])) 
 	  return mid
 	else if(array[mid] < array[mid-1]) 
 	  end=mid-1
 	else 
 	  start=mid+1
 	end if
     end while
     
end efficientPeak
 

Time Complexity: O(log n)
Auxillary Space: O(1)