|
| 1 | +{% include list.liquid all=true %} |
| 2 | + |
| 3 | +## Mobius Strip |
| 4 | + |
| 5 | +There are some mathematical shape of this residual objects. [Torus](https://gist.github.com/eq19/e9832026b5b78f694e4ad22c3eb6c3ef#the-crank-of-a-partition) is basically a donut shape, which has the property of of having variable Gaussian curvature. |
| 6 | + |
| 7 | +```note |
| 8 | +The blue parts of the torus above have positive curvature, the red parts negative and the top grey band has zero curvature. If our 3 dimensional space was like the surface areas of a 4 dimensional torus, the parts would have different angle sums. |
| 9 | +``` |
| 10 | + |
| 11 | +[](https://gist.github.com/eq19/e9832026b5b78f694e4ad22c3eb6c3ef#the-crank-of-a-partition) |
| 12 | + |
| 13 | +Some parts of the surface has positive curvature, others zero, others negative. |
| 14 | + |
| 15 | + |
| 16 | + |
| 17 | +If you start anywhere on its surface and follow the curvature round you will eventually return to the same place having travelled on every part of the surface. |
| 18 | + |
| 19 | + |
| 20 | + |
| 21 | + |
| 22 | + |
| 23 | +Mobius strip only has one side, there are two more bizarre shapes with strange properties. |
| 24 | + |
| 25 | +## The Klein bottle |
| 26 | + |
| 27 | +The Klein bottleis in someways a 3D version of the Mobius strip and even though it exists in 3 dimensions, to make a true one you need to “fold through” the 4th dimension. |
| 28 | + |
| 29 | +```note |
| 30 | +In [mathematics](https://en.wikipedia.org/wiki/Mathematics), the Klein bottle ([/ˈklaɪn/](https://en.wikipedia.org/wiki/Help:IPA/English)) is an example of a [non-orientable](https://en.wikipedia.org/wiki/Orientability) [surface](https://en.wikipedia.org/wiki/Surface_(topology)); that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. |
| 31 | +- More formally, the Klein bottle is a [two-dimensional](https://en.wikipedia.org/wiki/Two-dimensional) [manifold](https://en.wikipedia.org/wiki/Manifold) on which one cannot define a [normal vector](https://en.wikipedia.org/wiki/Normal_vector) at each point that varies [continuously](https://en.wikipedia.org/wiki/Continuous_function) over the whole manifold. |
| 32 | +- Other related non-orientable surfaces include the [Möbius strip](https://en.wikipedia.org/wiki/M%C3%B6bius_strip) and the [real projective plane](https://en.wikipedia.org/wiki/Real_projective_plane). |
| 33 | +
|
| 34 | +While a Möbius strip is a surface with a [boundary](https://en.wikipedia.org/wiki/Boundary_(topology)), a Klein bottle has no boundary. For comparison, a [sphere](https://en.wikipedia.org/wiki/Sphere) is an orientable surface with no boundary. |
| 35 | +``` |
| 36 | + |
| 37 | +[](https://en.wikipedia.org/wiki/Klein_bottle) |
| 38 | + |
| 39 | +[](https://ibmathsresources.com/2014/08/05/non-euclidean-geometry-v-theshapeoftheuniverse/) |
| 40 | + |
| 41 | +A sign inversion visualized as a vector pointing along the [Möbius band](https://en.wikipedia.org/wiki/M%C3%B6bius_band) when the circle is continuously rotated through a full turn of 360°. |
| 42 | + |
| 43 | +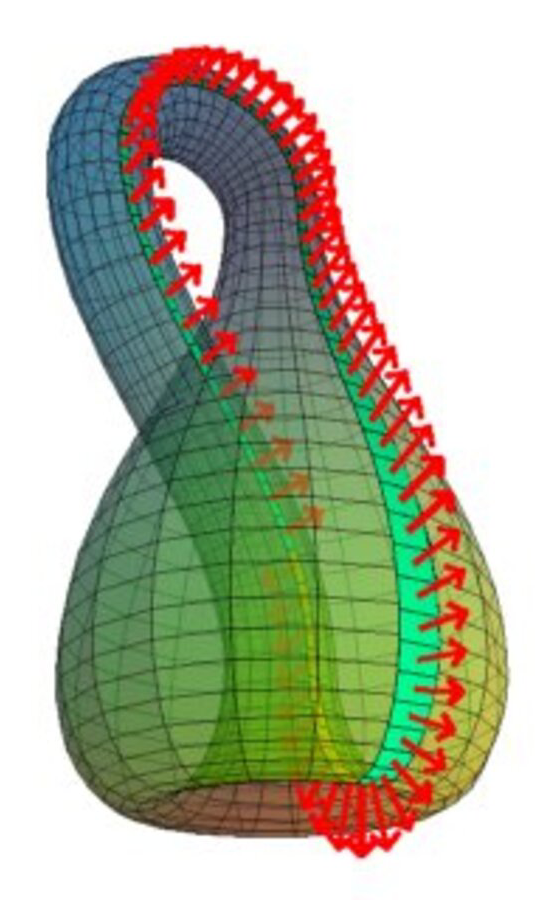 |
| 44 | + |
| 45 | +## The Spinors |
| 46 | + |
| 47 | +A spinor associated to the conformal group of the circle, exhibiting a sign inversion on a full rotation of the circle through an angle of 2π. |
| 48 | + |
| 49 | +***(17+13) + (11+19) = (7+11) + (19+23) = 60*** |
| 50 | + |
| 51 | +[](https://en.wikipedia.org/wiki/Dirac_spinor#Four-spinor_for_particles) |
| 52 | + |
| 53 | +[](https://youtu.be/4NJBvkjpC3E) |
| 54 | + |
| 55 | + |
| 56 | + |
| 57 | +```note |
| 58 | +Eigennvalue curves (right) showing a triple eigenvalue at zero for τ = 1 and double eigenvalues at 1 ± √2i for τ = √43. On the left the graph of 1/|Q(λ)| with the same eigenvalue curves plotted in the ground plane. Green stars indicate the eigenvalues of A, blue stars the roots of puv(λ) and triangles the zeroes of Q0 |
| 59 | +(λ) |
| 60 | +``` |
| 61 | + |
| 62 | +## Global Properties |
| 63 | + |
| 64 | +***7 + 11 + 13 = 31*** |
| 65 | +***1 + (26+6) + (27+6) = 66*** |
| 66 | + |
| 67 | +[](https://www.hexspin.com/0-1-and-negative-numbers/) |
| 68 | + |
| 69 | +```txt |
| 70 | + 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 71 | +---+---+---+---+---+---+---+---+---+---+----+----+----+----+----+----+----+---- |
| 72 | + - | - | 20| 21| 22| 23| 24| 25| |
| 73 | +---+---+---+---+---+---+---+---+ |
| 74 | + - | - | - | - | 28| 29| ◄--- missing 26 & 27 ✔️ |
| 75 | +---+---+---+---+---+---+ |
| 76 | + 30| 31| - | - | ◄--- missing 32 & 33 ✔️ |
| 77 | +---+---+---+---+ |
| 78 | + 36| |
| 79 | +``` |
| 80 | + |
| 81 | +```tip |
| 82 | +This behaviour finaly brings us to a suggestion that the dimension in string theory are linked with ***the prime distribution level*** as indicated by the _[self repetition](https://www.eq19.com/exponentiation/#self-repetition)_ on MEC30. |
| 83 | +``` |
| 84 | + |
| 85 | +***7th spin - 4th spin = (168 - 102)s = 66s = 6 x 11s = 30s + 36s*** |
| 86 | + |
| 87 | +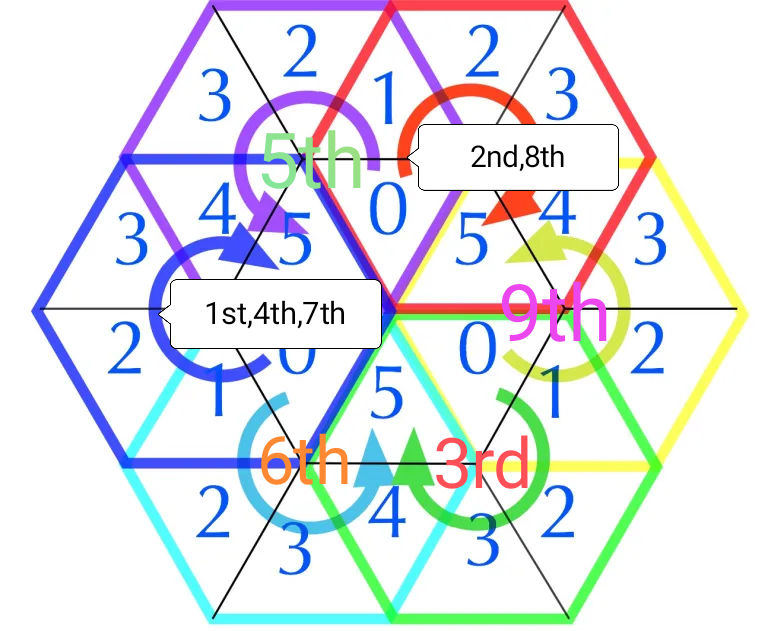 |
| 88 | + |
| 89 | +```txt |
| 90 | +$True Prime Pairs: |
| 91 | +(5,7), (11,13), (17,19) |
| 92 | + |
| 93 | +layer | node | sub | i | f. MEC 30 / 2 |
| 94 | +------+------+-----+-----+------ ‹------------------------------ 0 {-1/2} |
| 95 | + | | | 1 | -------------------------- |
| 96 | + | | 1 +-----+ | |
| 97 | + | 1 | | 2 | (5) | |
| 98 | + | |-----+-----+ | |
| 99 | + | | | 3 | | |
| 100 | + 1 +------+ 2 +-----+---- | |
| 101 | + | | | 4 | | |
| 102 | + | +-----+-----+ | |
| 103 | + | 2 | | 5 | (7) | |
| 104 | + | | 3 +-----+ | |
| 105 | + | | | 6 | 11s ‹-- ∆28 = (71-43) √ |
| 106 | +------+------+-----+-----+------ } (36) | |
| 107 | + | | | 7 | | |
| 108 | + | | 4 +-----+ | |
| 109 | + | 3 | | 8 | (11) | |
| 110 | + | +-----+-----+ | |
| 111 | + | | | 9 |‹-- ∆9 = (89-71) / 2 √ | |
| 112 | + 2 +------| 5* +-----+----- | |
| 113 | + | | | 10 | | |
| 114 | + | |-----+-----+ | |
| 115 | + | 4 | | 11 | (13) --------------------- |
| 116 | + | | 6 +-----+ ‹------------------------------ 15 {0} |
| 117 | + | | | 12 |--------------------------- |
| 118 | +------+------+-----+-----+------------ | |
| 119 | + | | | 13 | | |
| 120 | + | | 7 +-----+ | |
| 121 | + | 5 | | 14 | (17) | |
| 122 | + | |-----+-----+ | |
| 123 | + | | | 15 | 7 x 24 = 168 √ |
| 124 | + 3* +------+ 8 +-----+----- } (36) | |
| 125 | + | | | 16 | | |
| 126 | + | |-----+-----+ | |
| 127 | + | 6 | | 17 | (19) | |
| 128 | + | | 9 +-----+ | |
| 129 | + | | | 18 | -------------------------- |
| 130 | +------|------|-----+-----+----- ‹----------------------------------- 30 {+1/2} |
| 131 | +``` |
| 132 | + |
| 133 | +This model may explains the newly discovered prime number theorem in relatively simple layman's terms for anyone with a slight background in theoretical physics. |
| 134 | + |
| 135 | +```note |
| 136 | +The property gives an in depth analysis of the not so random distribution of primes by showing how it has solved Goldbach's conjecture and the Ulam spiral. |
| 137 | +``` |
| 138 | + |
| 139 | +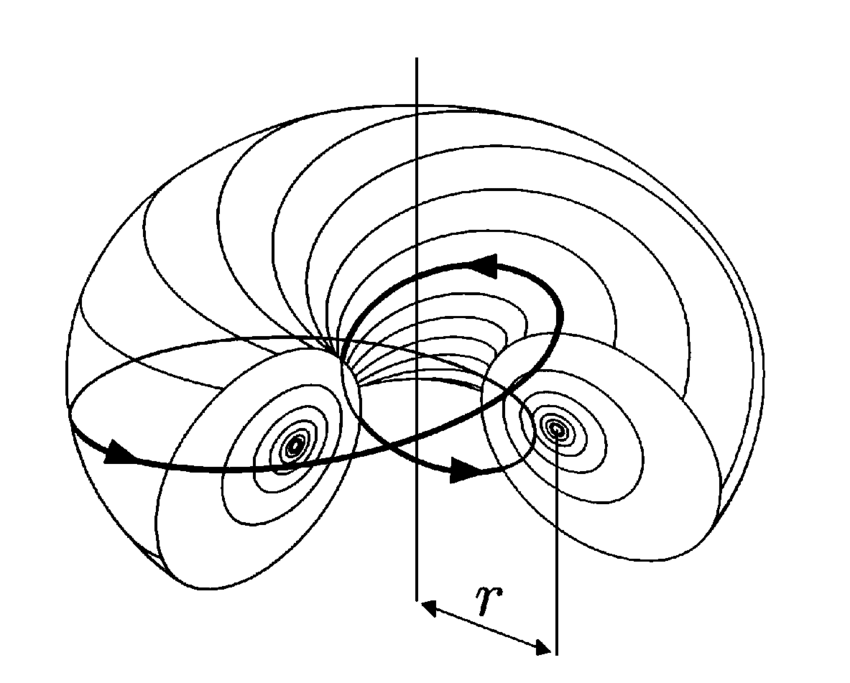 |
| 140 | + |
| 141 | +The model suggests a possible origin for both charge and half-integer spin and also reconciles the apparently contradictory criteria discussed above. |
| 142 | + |
| 143 | +```note |
| 144 | +***Arbitrary sequence of three (3) consecutive nucleotides*** along a helical path whose metric distances satisfy the relationship dn,n+3�dn,n+2�dn,n+1. |
| 145 | +- Sketch showing a characteristic duplex DNA helical standing-wave pattern. |
| 146 | +- The vertical lines depict the cross-section projections of each bp along the helix axis, their length providing a measure of their twist magnitude. |
| 147 | +- Thick lines represent the sugar-phosphate profile. |
| 148 | +
|
| 149 | +Optimally overlapping bps are indicated by the presence of the ovals (m) measures the �overlapping resonance correlation length. _([π − π orbital resonance in twisting duplex DNA](https://github.com/eq19/eq19.github.io/files/13790206/prb_Hx2.pdf))_ |
| 150 | +``` |
| 151 | + |
| 152 | +[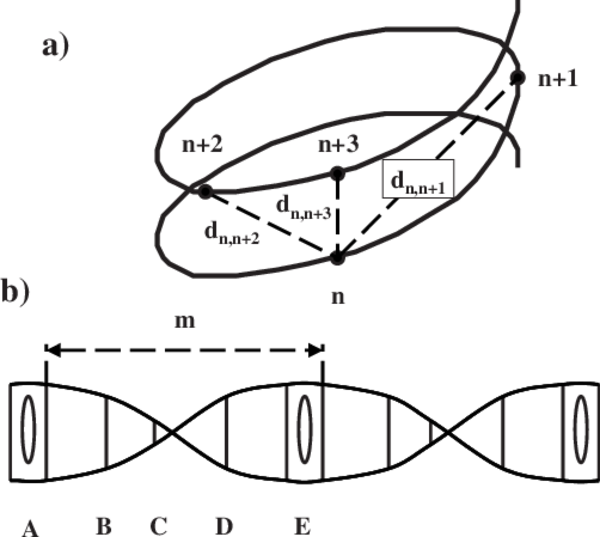](https://github.com/eq19/eq19.github.io/files/13790206/prb_Hx2.pdf) |
| 153 | + |
| 154 | +Under certain conditions, energy could not take on any indiscriminate value, the energy must be some multiple of a very small quantity (later to be known as a ***quantum***). |
| 155 | + |
| 156 | +```note |
| 157 | +Twisted strip model for one wavelength of a photon with circular polarisation in at space. A similar photon in a closed path in curved space with periodic boundary conditions of length �C. |
| 158 | +
|
| 159 | +- The B-fi�eld is in the plane of the strip and the E-field� is perpendicular to it (a). |
| 160 | +- The E-fi�eld vector is radial and directed inwards, and the B-fi�eld is vertical (b). |
| 161 | +
|
| 162 | +The magnetic moment ~�, angular momentum L~, and direction of propagation with velocity c are also indicated. _([Is the electron a photon with toroidal topology? - pdf](https://github.com/eq19/eq19.github.io/files/13790325/LdBelectoroid.pdf))_ |
| 163 | +``` |
| 164 | + |
| 165 | +[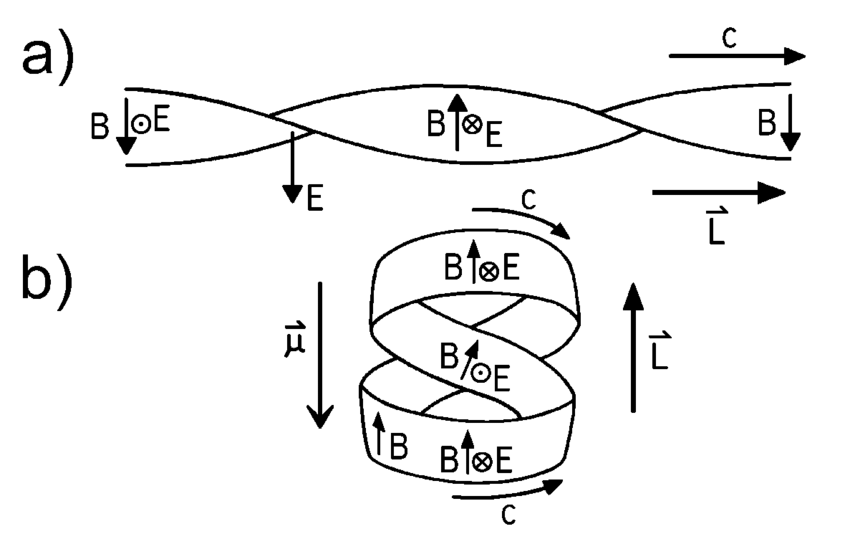](https://github.com/eq19/eq19.github.io/files/13790325/LdBelectoroid.pdf) |
| 166 | + |
| 167 | +A deeper understanding requires a uni�cation of the aspects discussed above in terms of an underlying principle. |
0 commit comments