-
Notifications
You must be signed in to change notification settings - Fork 26
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
the formulea for calculating derivatives of different error orders #204
Comments
|
Hey @thudjx! Would you be able to share the function you're trying to estimate the derivative of? To answer your questions, To improve the accuracy of the estimate, you have a few knobs that you can play with. (Some of these you have already tried, but I'll include them anyway for completeness.)
|
|
Thanks for your kind reply! It does help a lot, especically the mensioned I have tried different I have extracted the codes for calculating finite difference from my project and uploaded here. The dependences of functions seem to be deep, but the main function is to calculate the derivative over To sum, my main problem now is how to determine if the obtained derivative has converged. And I would really appreciate it if you could explain more on how the |
|
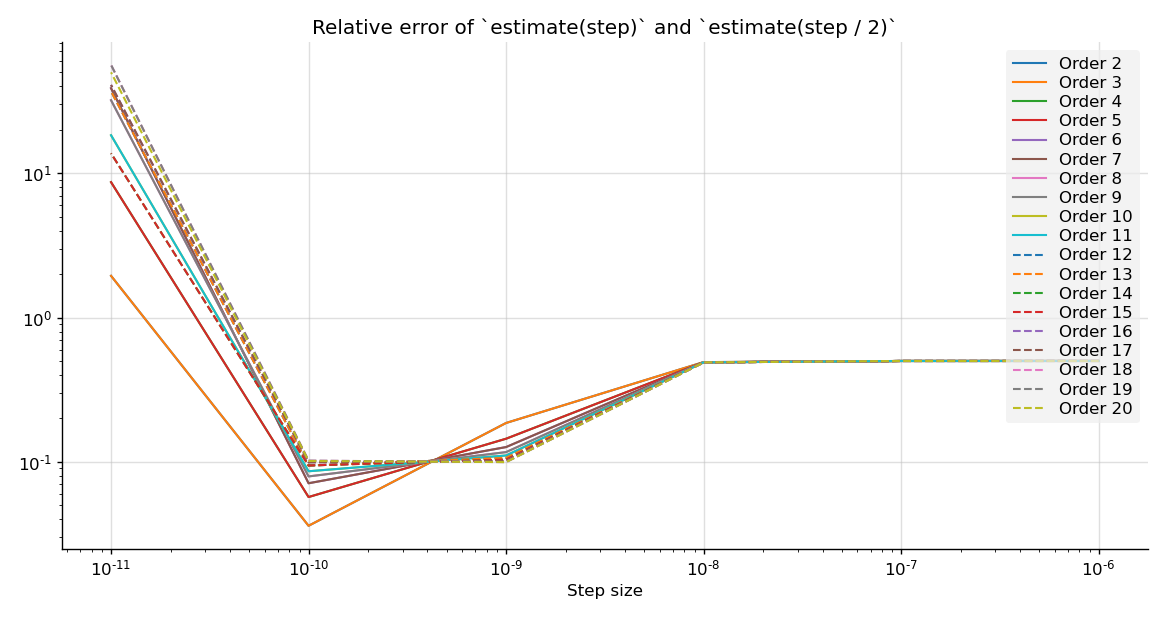
Thanks for uploading the function! I've played around with it, and it seems like a derivative which is really hard to estimate. To try to get somewhere, I ran a loop comparing, for various orders and manual step sizes, the relative error of for order in [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
for step in [1e-6, 1e-7, 1e-8, 1e-9, 1e-10, 1e-11]
deriv = central_fdm(order, 1, adapt=0)(df, 0, step)
deriv2 = central_fdm(order, 1, adapt=0)(df, 0, step / 2)
println("order ", order, " step ", step)
println("rel err ", maximum(abs.((deriv .- deriv2) ./ deriv2)))
end
endThe results are as follows: From these results I think we can possibly say that central_fdm(3, 1, adapt=0)(df, 0, 1e-10)gives the derivative with a relative error of at most ~5–10%. Maybe. You can extend the above experiment to find the best step size with better accuracy. I'm thinking that just calling julia> (central_fdm(3, 1)(df, 0) - central_fdm(3, 1)(df, 1e-8)) ./ central_fdm(3, 1)(df, 0)
148-element Vector{Float64}:
-1.4334788909465992e-5
4.19189206515889e-5
1.7207500832533594e-5
1.720758162247681e-5
7.056494918595109e-7
7.682371633023401e-7
0.010735984423210845
0.010735984353677543
0.005944599044609511
0.005944599021037245
0.016398963883520877
0.01639896356214377
-4.152377378291932e-5
-4.400792286950248e-5
4.122025356174162e-5
4.122962192413027e-5
-8.356807216090289e-5
6.67547642864647e-5
6.675479621986351e-5
1.0483810653899413e-5
1.0483672464959598e-5
3.7624599200651645e-7
3.597428654570998e-7
-2.3663300431130233e-9
-1.4505077031791408e-8
⋮
-5.1859371908231306e-8
-4.1797550211563575e-8
4.2357701426808593e-7
2.513691130573262e-7
1.8318761071411643e-7
-2.8739623963281802e-9
0.002688363928732466
0.002688364042537789
-1.2049749539114263e-6
0.001469467549865613
0.0014694675608115221
6.919078855483783e-6
6.91907218090512e-6
-1.7728215864604077e-7
0.03384961097002314
0.03384961115382243
0.02345264321077442
0.02345264330738625
1.0768199313377127e-6
1.0767593229996247e-6
4.533637943871176e-7
4.5046856739853824e-7
0.0802908770638142
0.08029087690465797
-3.994830494965322e-6From this it looks like the estimate works well for elements 1 to 6, but fails e.g. at the 7th. This also shows here: julia> central_fdm(3, 1)(x -> df(x)[7], 0)
381973.2416938875
julia> central_fdm(5, 1)(x -> df(x)[7], 0)
2545.0107083557023Two completely different answers. However, now compare julia> central_fdm(3, 1)(x -> df(x)[7], 0, 1e-9)
416261.4394758179
julia> central_fdm(3, 1)(x -> df(x)[7], 0, 0.5e-9)
416270.4106676074
julia> central_fdm(5, 1)(x -> df(x)[7], 0, 1e-9)
416276.7878588269
julia> central_fdm(5, 1)(x -> df(x)[7], 0, 0.5e-9)
416273.4010644264which all look very similar! I think we can conclude that the determination of the step size fails here. And the reason for this, I think, is that at the very beginning of the step size procedure, it chooses a default step size which is too large. We can (sort of) fix this by setting julia> central_fdm(3, 1, max_range=1e-7)(x -> df(x)[7], 0)
416217.43166217837
julia> central_fdm(5, 1, max_range=1e-7)(x -> df(x)[7], 0)
416289.2128946737
julia> central_fdm(10, 1, max_range=1e-7)(x -> df(x)[7], 0)
416280.2540261937And now for the whole derivative: julia> central_fdm(10, 1, max_range=1e-7)(df, 0)
148-element Vector{Float64}:
0.05454670451807623
-0.027148598288693086
14927.057274862253
-14927.047748153713
54.56887273995019
-54.546313241034895
416278.2298787704
-416278.23286688176
2.5523083553546857e7
-2.552308356486684e7
671274.6657252071
-671274.6785747902
0.02807019678057646
0.020856330257093735
19134.20051677652
-19132.64030938499
-1.570973683297297
37145.68973011968
-37145.698490679046
12866.57077194119
-12866.566537586232
131.3512936174559
-131.31100440007447
5.693078042210595
-5.65363796828887
⋮
103.8471606229204
-103.86459279665155
0.06727649172635625
66.34951781544139
-66.38988965296109
-0.11228568365274279
240423.27082720457
-240423.26070539176
-0.014211765907845288
5.6352528503405556e7
-5.635252848006791e7
11797.193874745062
-11797.189899861567
-0.026747502409681958
1.0142252038092563e7
-1.0142252022824168e7
1.2026662874248665e7
-1.2026662863188127e7
1880.4665790017198
-1880.483115881209
14.856149949766118
-14.883831603066223
3.4196170336767444e6
-3.4196170373332505e6
-0.01321809613942529julia> maximum((central_fdm(10, 1, max_range=1e-8)(df, 0) .- central_fdm(11, 1, max_range=1e-8)(df, 0)) ./ central_fdm(10, 1, max_range=1e-8)(df, 0))
0.07342207122310172A better solution is probably to use a scaled version of julia> maximum((central_fdm(5, 1)(x -> df(1e-6 * x), 0) .* 1e6 - central_fdm(7, 1)(x -> df(1e-6 * x), 0) .* 1e6) ./ (central_fdm(5, 1)(x -> df(1e-6 * x), 0) .* 1e6))
0.08432044412807255I think something like this might work for you. You can prob squeeze more out of it by optimising the order of the method and further playing with the parameters to really get the best step size. An interesting questions is whether the procedure to determine the step size automatically can be improved to also be robust in cases like this. |
|
Thanks for your reply! I do have learned a lot from your posts here! I am still not clear why there are so many divergent value components. I thought this may be caused by numerical errors. Thus I tried to use I have tried to use So the last hope for me now is to detect where the numerical divergence comes from(the effeciency of But before that, I have to understand how the |
Ah, it seems that I converged onto a very wrong local optimum in my investigation above. 😅
Numerical errors can indeed really mess with the estimates of finite differences. Are you 100% sure that there is no error in the implementation of If you want to use finite differences, one thing you can do is to do is to look at
The package assumes that the error on function evaluations |
Sorry to misuse issues to ask questions, but I could't find any other way to communicate with you developers.

I am using this package to calculate the first order derivative of a matrix which can be thought of a function of mono variable x, i.e., M(x). I find that the derivative is hard to converge. By converging I mean if I add more nodes when calculating the derivative, the derivative is unchanged under some tolerance. In practice, I just increase
qincentral_fdm(q, 1).I have tried
qup to 12 but the result didn't seem to convergence. I couldn't increse the order any more because the time for calculation is unacceptable in my case.I also tried to change
max_range, and the result is quite different from that calculated with defaultmax_range.That led me to investigate the details of calculating method of
FiniteDifferences.jl. I found that the method for calculating derivative in this package is not that easy to understand, especially I find that it choose nodes of two different set.(see picture below)So would you please give some more details on how the nodes are chosen, especially the meaning of
max_rangeand how are the derivatives calculated using the nodes?The text was updated successfully, but these errors were encountered: