pyTaylor: Mathematical Functions via Taylor Series

Overview

pyTaylor is a Python package that explores classical mathematical functions through series expansions and analytical approximations. It aims to provide a research-oriented framework for studying, comparing, and visualizing functions like sine, cosine, exponential, logarithm, and square roots, highlighting the accuracy and convergence of Taylor series and other mathematical formulas.

This package includes:

• sin(x) – Sine function using Taylor series.
• cos(x) – Cosine function using Taylor series.
• tan(x) – Tangent function using Taylor series.
• exp(x) – Exponential function using Taylor series.
• log(x) – Natural logarithm using Taylor series.
• sqrt(x) – Square root function using series approximation.
• factorial(n) – Factorial using Stirling's approximation.
• constants.py – Common mathematical constants.
• utils.py – Utility functions such as argument normalization.

---

Formulas Used

1. Sine

$$ \sin(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} $$

2. Cosine

$$ \cos(x) \approx 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} $$

3. Tangent

$$ \tan(x) \approx x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 $$

4. Exponential

$$ e^x \approx 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} $$

5. Natural Logarithm (ln)

$$ \ln(1+x) \approx x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots $$

6. Square Root

$$ \sqrt{1+x} \approx 1 + \frac{x}{2} - \frac{x^2}{8} + \frac{x^3}{16} - \frac{5x^4}{128} + \dots $$

7. Factorial (Stirling's Approximation)

$$ n! \approx \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n \left( 1 + \frac{1}{12n} \right) $$

---

Example Usage

from mymath.sin import sin
from mymath.cos import cos
from mymath.factorial import factorial

print(sin(30))       # sine in degrees
print(cos(60))       # cosine in degrees
print(factorial(10)) # approximate factorial

You can also visualize the functions and compare them with Python's math library using matplotlib examples in the examples/ folder.

Function Comparison Visualizations

The following plots illustrate the comparison between the Taylor series approximations implemented in this package and the standard Python math library functions. These visualizations help to understand the accuracy and behavior of the approximations.

Sine Function

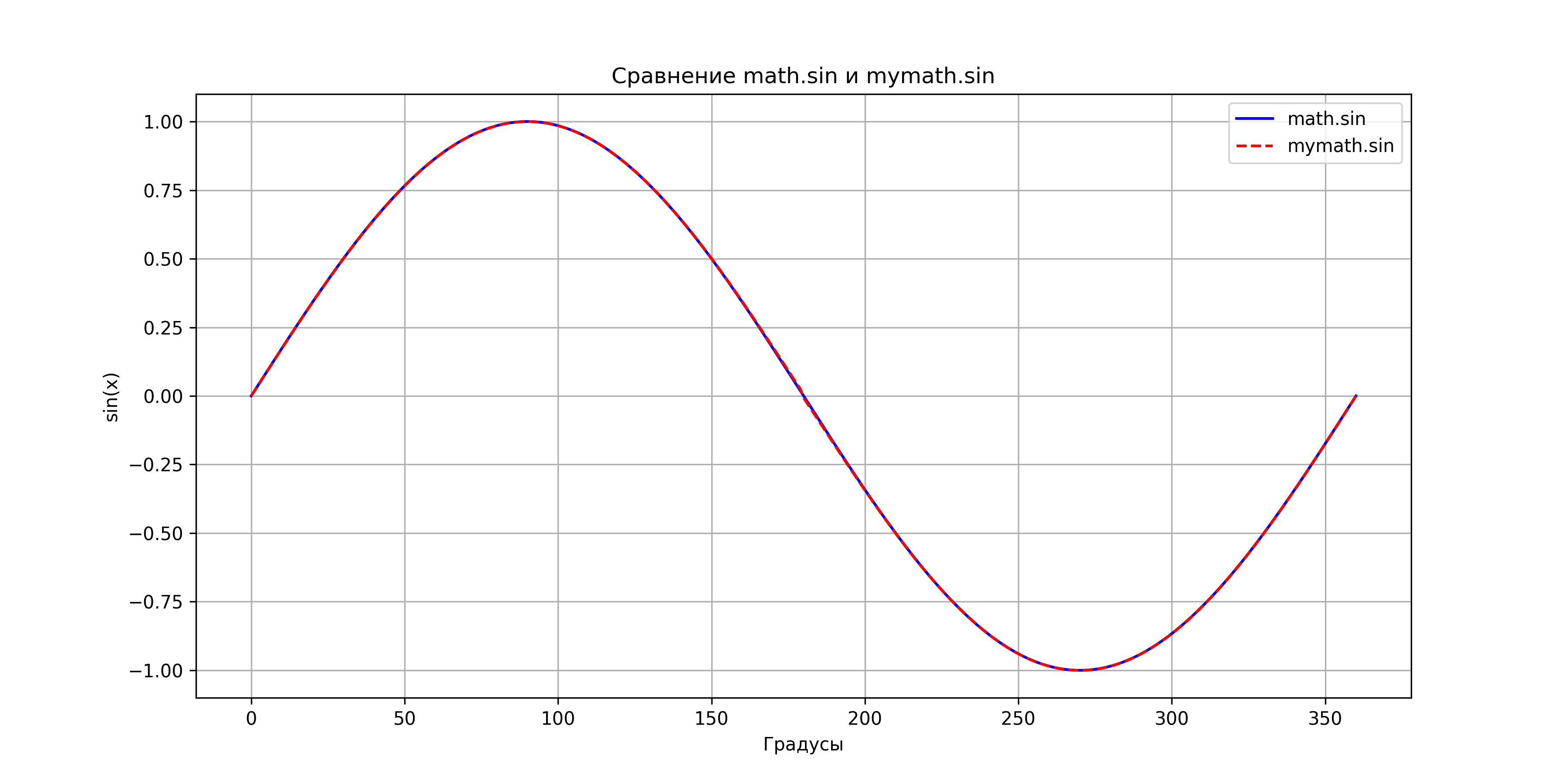
Comparison of mymath.sin vs math.sin.

Cosine Function

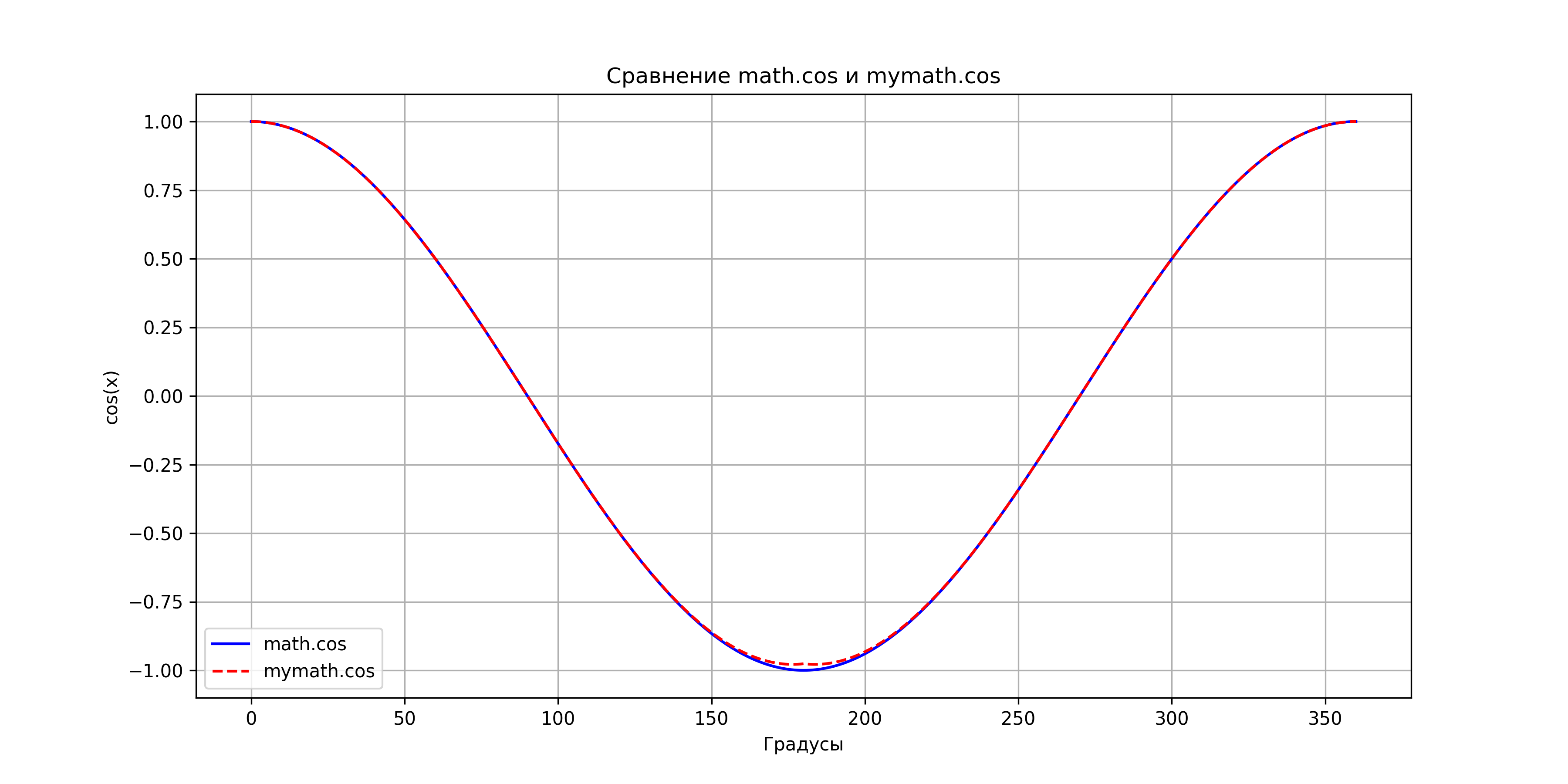
Comparison of mymath.cos vs math.cos.

Tangent Function

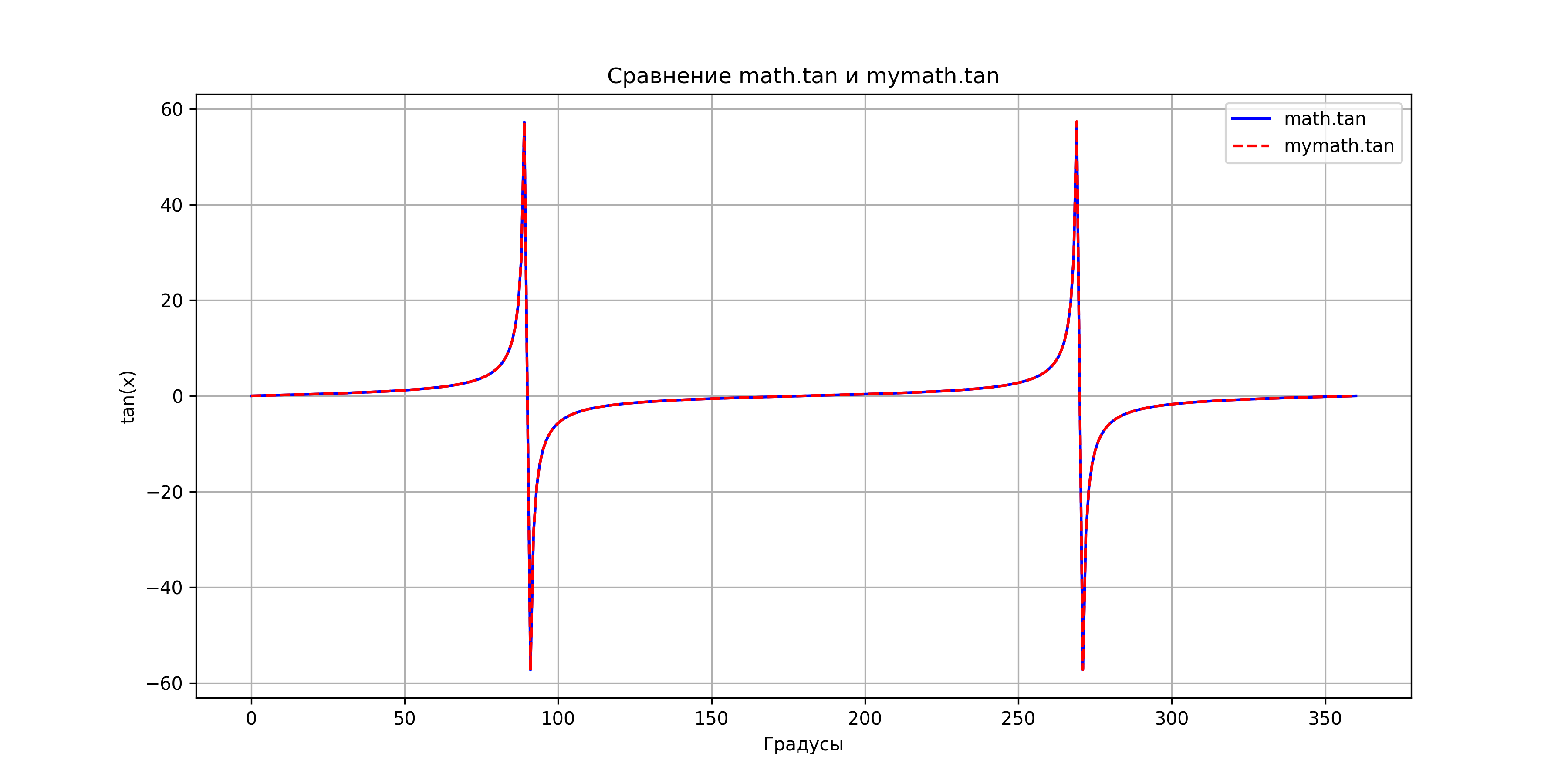
Comparison of mymath.tan vs math.tan.

Exponential Function

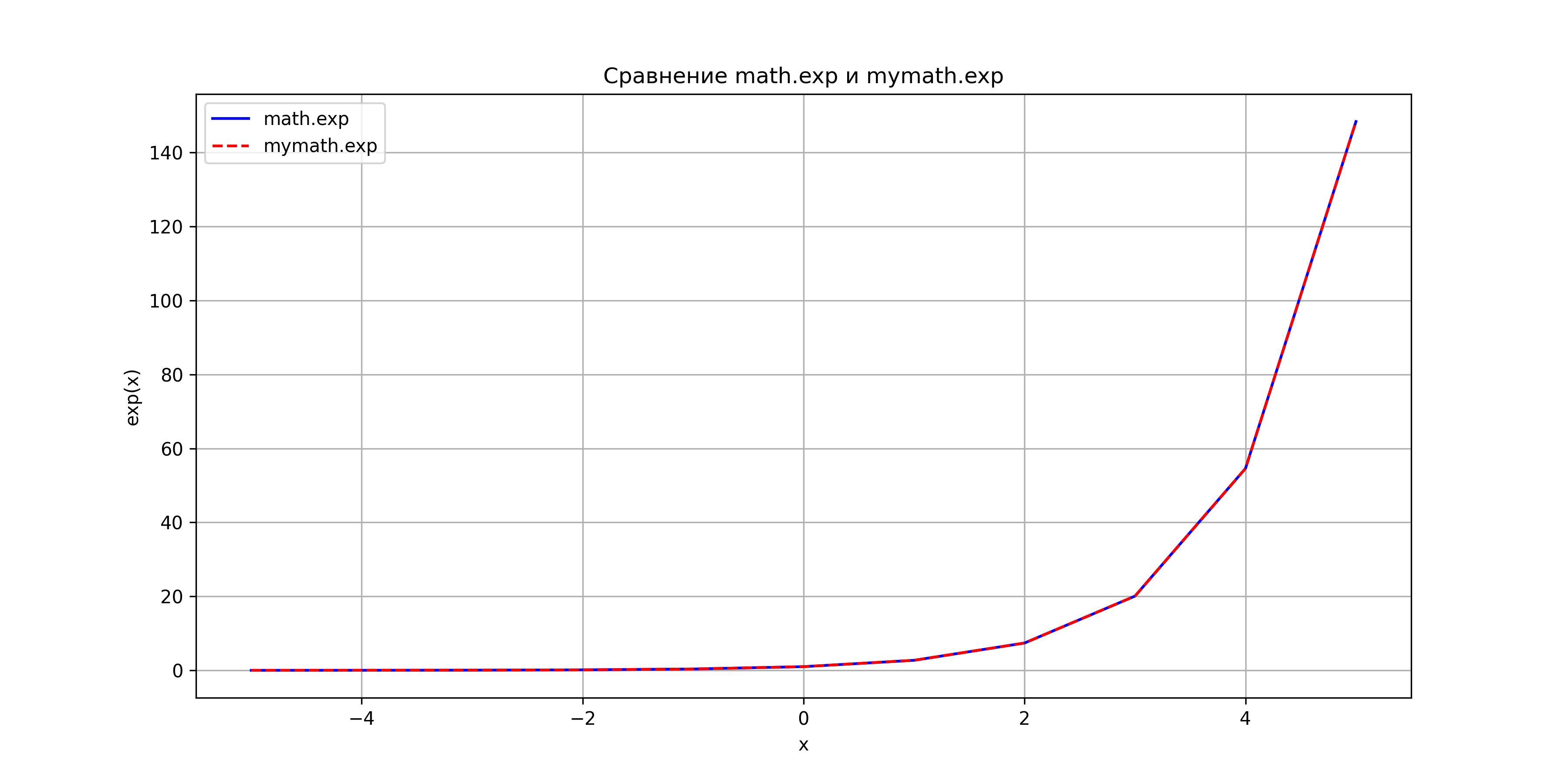
Comparison of mymath.exp vs math.exp.

Natural Logarithm Function

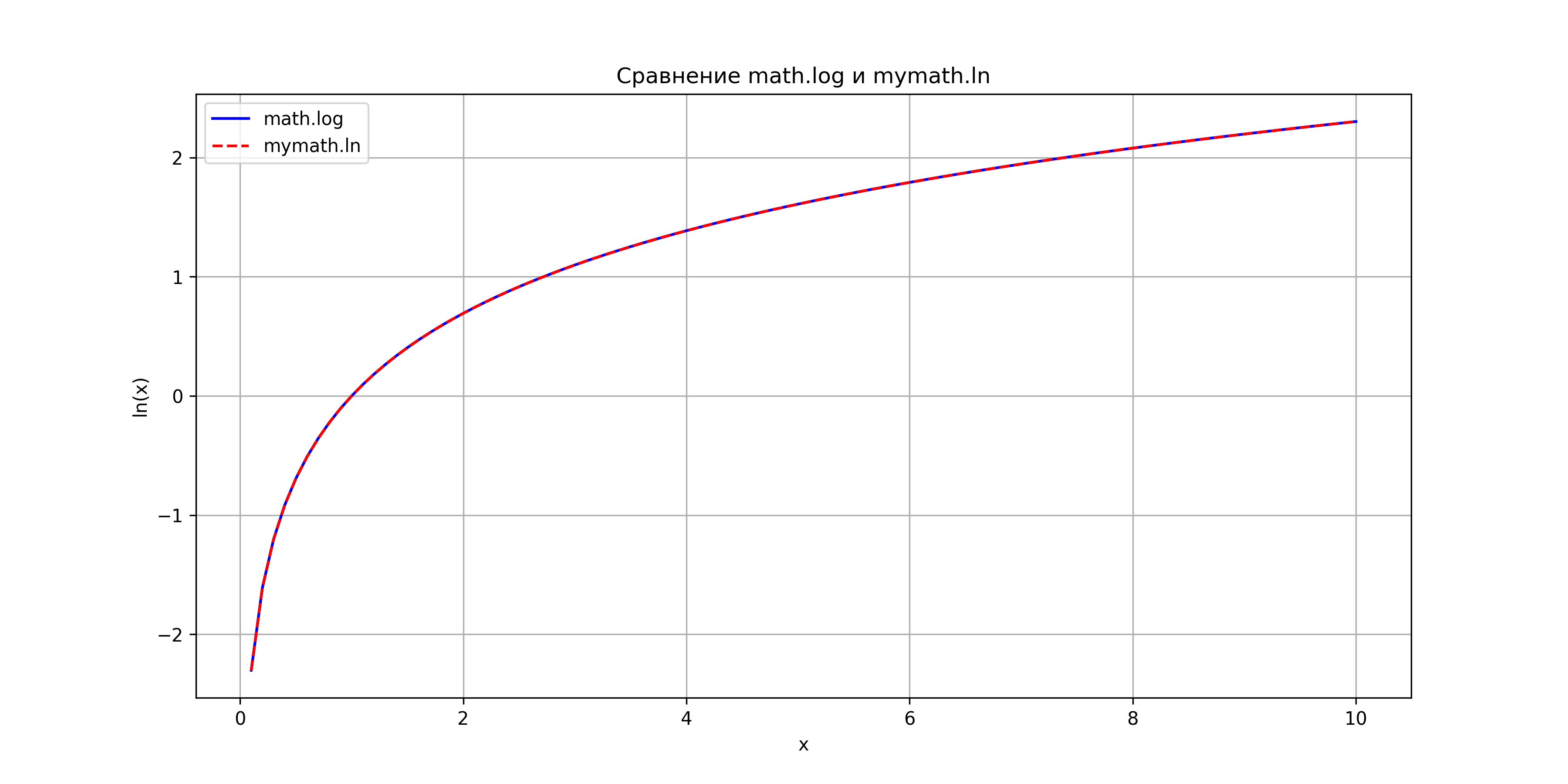
Comparison of mymath.log vs math.log.

Square Root Function

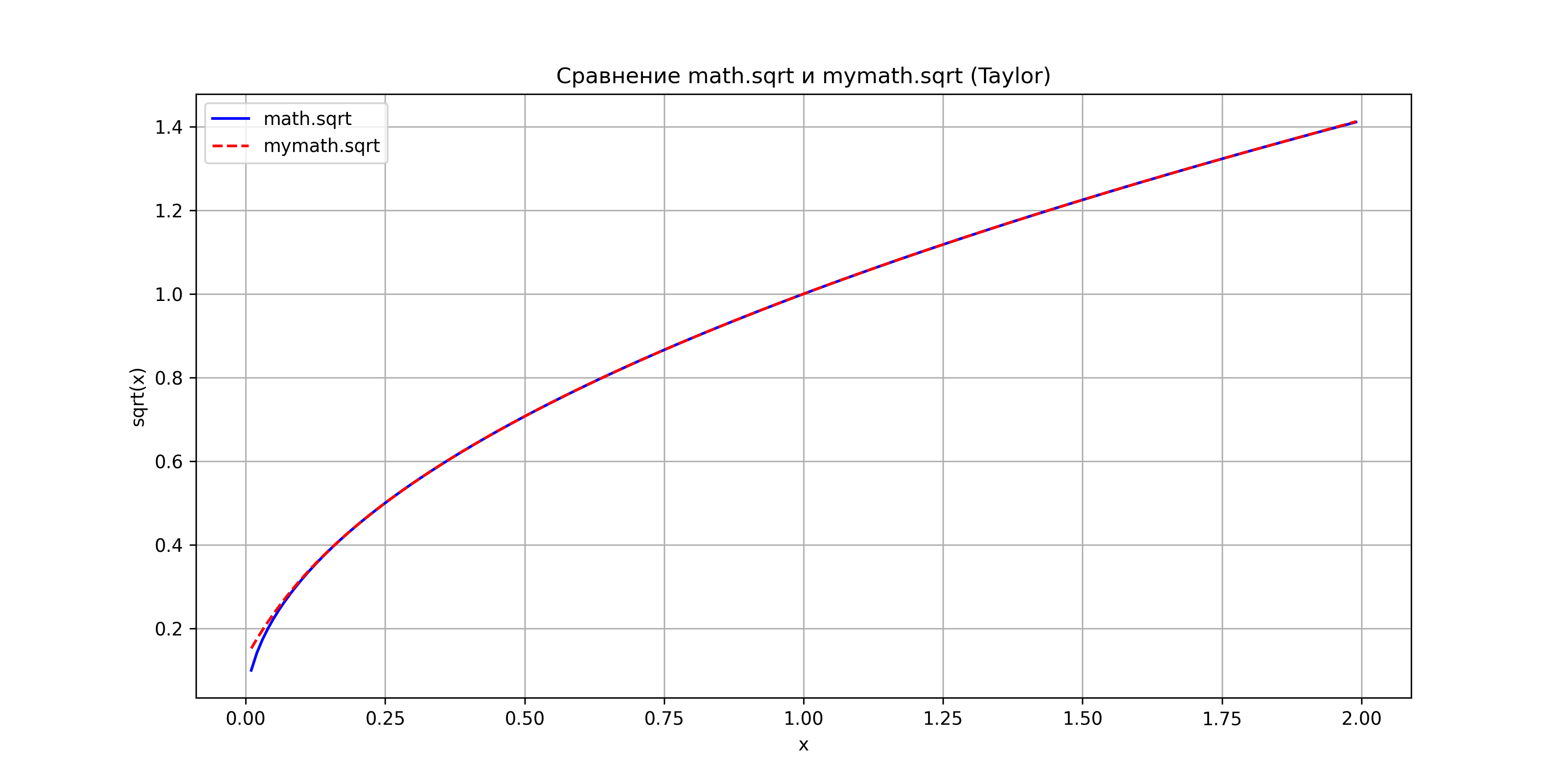
Comparison of mymath.sqrt vs math.sqrt.

---

These plots demonstrate the effectiveness of Taylor series and classical approximations for common mathematical functions over typical ranges.

---

License

This project is licensed under the MIT License.

---

Notes

• Input angles are in degrees and normalized internally to radians.
• For factorials, Stirling's formula provides fast approximation, especially useful for large numbers.
• This project is intended for educational and research purposes.