07-卡尔曼滤波原理（七）平方根Kalman滤波：Potter平方根滤波、SVD分解滤波、UD分解滤波、平方根信息滤波SRIKF.md

[TOC]

常见矩阵分解简介：

• LU分解：$M=LU$ ，$L$ 是下三角矩阵，$U$ 是上三角矩阵。方便求矩阵的行列式和逆，解线性方程组。
• Cholesky分解：$M=L^TL$ ，$L$ 是上三角矩阵。是LU分解的进阶版。但是不同于LU分解的是，Cholesky分解只适用于正定的对称阵。在复数域，Cholesky分解要求矩阵是正定的共轭对称矩阵。要求这么多，就是因为Cholesky分解可以看成是给矩阵开平方根。
• QR分解：$M=QR$ ，其中 $Q$ 是正交矩阵，$R$ 是上三角矩阵。主要有三种方法：Gram-Schmidt正交化法（QR分解中的Q本身就可以看作是正交化构造出来的），Household变换法，Givens变换法。 可以用来求矩阵的特征值以及求解最小二乘法。
• 特征值分解：$M=VDV^T$ ，其中 $V$ 是正交阵，$D$ 是由 $M$ 的特征值构成的对角矩阵。只适用于方阵，目的是提取出矩阵最重要的特征。
• 奇异值分解（SVD分解）：$M=USV^T$ ，其中 $U$、$V$ 是正交矩阵，$S$ 是由 $M$ 的奇异值构成的对角矩阵。特征值分解只适用于方阵，对于普通矩阵，则可以采用奇异值分解，提取出奇异值。
• UD分解：$M=UDU^T$，$U$ 为上三角且对角线元素为 $1$，$D$ 为对角阵

一、平方根滤波基本形式

在计算机中，单精度浮点数(float)有效数字为7位，双精度 (double)为16位，为了提高前者环境下的均方差阵计算精度，须采用平方根滤波。Kalman滤波计算过程中，有三个方差阵，分别可以记为： $$ \begin{array}{l} \boldsymbol{{P}{k-1}}=\boldsymbol{U}{k-1} \boldsymbol{U}{k-1}^{\mathrm{T}}\\boldsymbol{P}{k / k-1}=\boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \\boldsymbol{P}{k}=\boldsymbol{U}{k} \boldsymbol{\Delta}_{k}^{\mathrm{T}} \end{array} $$

方差都可以表示成平方的形式，标量的平方直接拆成中误差的平方就行，矩阵的平方可以拆成一个矩阵乘以它的转置，最常见是表示成下三角阵乘上三角阵形式（Cholesky分解）。

标准Kalman滤波的流程图可以表示成：

将图中的 $P、Q、R$ 都用平方根形式替换 ，得：

• 更新都用平方根，损失精度小。
• 每一次滤波只计算一次增益矩阵 $K$ ，用于左边的滤波计算回路，而对右边的增益计算回路无影响，可以损失一点精度。

二、Potter平方根滤波

1、方差阵的量测更新

考虑量测为标量的情况，由标准Kalman滤波方差阵递推公式：

如果不是标量量测，就用序贯滤波的方法，一个个做滤波

$$ \begin{array}{l}\boldsymbol{K}{k}=\boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k}\right)^{-1} \ \boldsymbol{P}{k}=\left(\boldsymbol{I}-\boldsymbol{K}{k} \boldsymbol{H}{k}\right) \boldsymbol{P}{k / k-1}\end{array} $$

将 $K$ 带入第二个公式： $$ \boldsymbol{P}{k}=\boldsymbol{P}{k / k-1}-\boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}+R{k}\right)^{-1} \boldsymbol{H}{k} \boldsymbol{P}{k / k-1} $$ 将方差阵Cholesky分解，表示成平方根形式： $$ \begin{array}{l} \boldsymbol{\Delta}{k} \boldsymbol{\Delta}{k}^{\mathrm{T}}=\boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}}-\boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R{k}\right)^{-1} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \ =\boldsymbol{\Delta}{k / k-1}\left[\boldsymbol{I}-\boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}{\color{red}\left(\boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k}\right)}^{-1} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right] \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \\end{array} $$ 其中，$\boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R{k}$ 是标量，记为 $\rho_{k}^{2}$ ，可以在矩阵的前后随意移动，上式变为： $$ \boldsymbol{\Delta}{k / k-1}{\color{green}\left(\boldsymbol{I}-\rho{k}^{-2} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)} \boldsymbol{\Delta}_{k / k-1}^{\mathrm{T}} \quad $$

其中，绿色部分 $\left(\boldsymbol{I}-{\color{brown}\rho_{k}^{-2}} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)$ 的平方根分解：

取 $\gamma_{k}^{-1}$ 为待 定系数，写成分解的形式： $$ \begin{aligned}(\boldsymbol{I}- & \left.\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)\left(\boldsymbol{I}-\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)^{\mathrm{T}} \ & =\boldsymbol{I}-2 \gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}+\gamma_{k}^{-2} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \ & =\boldsymbol{I}-2 \gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}+\gamma_{k}^{-2} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}\left(\rho_{k}^{2}-R_{k}\right) \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1} \ & =\boldsymbol{I}-{\color{brown}\left[2 \gamma_{k}^{-1}-\left(\rho_{k}^{2}-R_{k}\right) \gamma_{k}^{-2}\right]} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\end{aligned} $$ 最后的式子和原式很相似，只差了棕色的部分，令棕色部分相等，可解待定系数 $\gamma_{k}^{-1}$ ： $$ \rho_{k}^{-2}=2 \gamma_{k}^{-1}-\left(\rho_{k}^{2}-R_{k}\right) \gamma_{k}^{-2} $$ 由： $$ \begin{array}{l} \rho_{k}^{-2}=2 \gamma_{k}^{-1}-\left(\rho_{k}^{2}-R_{k}\right) \gamma_{k}^{-2} \ \gamma_{k}^{2}-2 \rho_{k}^{2} \gamma_{k}+\rho_{k}^{2}\left(\rho_{k}^{2}-R_{k}\right)=0 \quad \rho_{k}^{2}=\boldsymbol{H}{k} \boldsymbol{\Delta}{k \mid k-1} \boldsymbol{\Delta}{k \mid k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k} \end{array} $$ 由于是二次，所以 $\gamma_{k}^{-1}$ 有两个解： $$ \gamma_{k}=\frac{2 \rho_{k}^{2} \pm \sqrt{4 \rho_{k}^{4}-4 \rho_{k}^{2}\left(\rho_{k}^{2}-R_{k}\right)}}{2}=\rho_{k}\left(\rho_{k} \pm \sqrt{R_{k}}\right) $$

将改部分进行分解： $$ \begin{aligned} \boldsymbol{\Delta}{k} \boldsymbol{\Delta}{k}^{\mathrm{T}} & =\boldsymbol{\Delta}{k / k-1}\left(\boldsymbol{I}-\rho{k}^{-2} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right) \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \ & =\boldsymbol{\Delta}{k / k-1}\left(\boldsymbol{I}-\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)\left(\boldsymbol{I}-\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)^{\mathrm{T}} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \ & =\left[\boldsymbol{\Delta}{k / k-1}\left(\boldsymbol{I}-\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)\right]\left[\boldsymbol{\Delta}{k / k-1}\left(\boldsymbol{I}-\gamma{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right)\right]^{\mathrm{T}} \end{aligned} $$ 得到方差阵的分解： $$ \boldsymbol{\Delta}{k}=\boldsymbol{U}{k / k-1}\left(\boldsymbol{I}-\gamma_{k}^{-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{H}{k} \boldsymbol{\Delta}{k / k-1}\right) $$ 实现方差阵的量测更新： $\boldsymbol{\Delta}{k / k-1}, \boldsymbol{R}{k}^{1 / 2} \longrightarrow \boldsymbol{\Delta}_{k}$

2、方差阵的时间更新

由标准Kalman滤波的时间更新： $$ \boldsymbol{P}{k / k-1}=\boldsymbol{\Phi}{k / k-1} \boldsymbol{P}{k-1} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}} $$ 写成分解形式： $$ \begin{array}{c}\boldsymbol{\Delta}{k / k-1} \boldsymbol{\Delta}{k / k-1}^{\mathrm{T}}=\boldsymbol{\Phi}{k / k-1} \boldsymbol{\Delta}{k-1} \boldsymbol{\Delta}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1}^{\frac{1}{2}}\left(\boldsymbol{Q}{k-1}^{\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}} \ =\left[\begin{array}{ll}\boldsymbol{\Phi}{k / k-1} \boldsymbol{\Delta}{k-1} & \boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1}^{\frac{1}{2}}\end{array}\right]\left[\begin{array}{c}\boldsymbol{\Delta}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}} \ \left(\boldsymbol{Q}{k-1}^{\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}}\end{array}\right]\end{array} $$

不能直接将 $\boldsymbol{\Phi}{k / k-1} \boldsymbol{\Delta}{k-1} \boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1}^{\frac{1}{2}}$ 作为 $\boldsymbol{\Delta}_{k / k-1}$ ，因为 $AA^T=BB^T$ 时，不能说 $A=B$

QR分解：列满秩矩阵 $A_{m*n}$ 总可以做QR分解：$\boldsymbol{A}{m \times n}=\hat{\boldsymbol{Q}}{m \times n} \hat{\boldsymbol{R}}{n \times n}$ 且有 $\hat{\boldsymbol{Q}}{m \times n}^{\mathrm{T}} \hat{\boldsymbol{Q}}{m \times n}=\boldsymbol{I}$ ，$\hat{\boldsymbol{R}}{n \times n}$ 是上三角可逆。

对上式QR分解： $$ \left(\hat{\boldsymbol{Q}}{2 n \times n} \hat{\boldsymbol{R}}{n \times n}\right)^{\mathrm{T}}\left({\hat{\boldsymbol{Q}}{2 n \times n} \hat{\boldsymbol{R}}{n \times n}}\right)={\boldsymbol{R}}{n \times n}^{\mathrm{T}} \hat{\boldsymbol{R}}{n \times n} $$

QR分解的改进：施密特正交化法，伪代码如下：

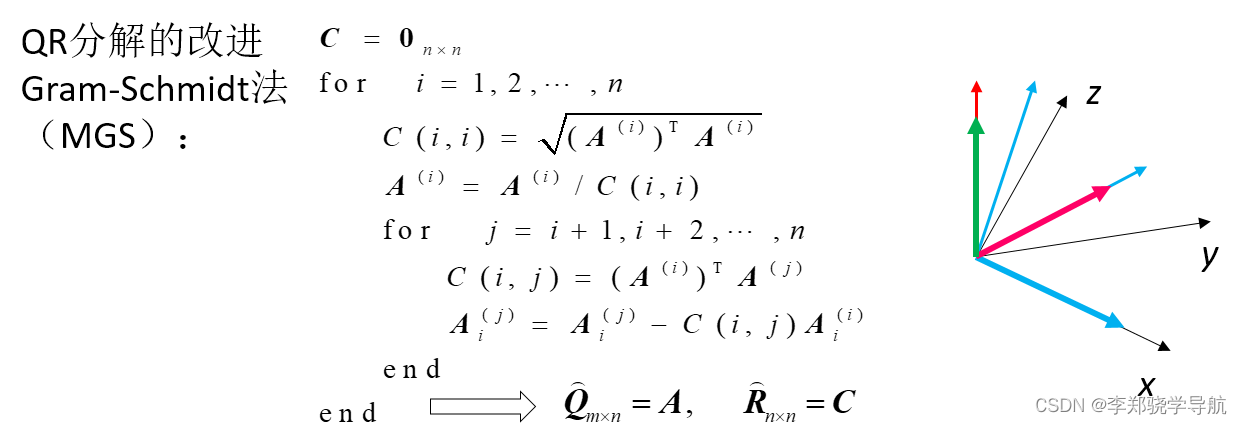
核心就是每个新的矢量都减去它在已经正交化的矢量方向的投影，进而每次新增一个新的正交矢量。新的矢量只和之前的矢量有关，而与后面的矢量无关。

先把 $\left[\begin{array}{c}\boldsymbol{\Delta}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}} \ \left(\boldsymbol{Q}{k-1}^{\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}}\end{array}\right]$ 求出来，再用Gram-Schmidt法即可得到方差阵的时间更新 $\boldsymbol{\Delta}_{k / k-1}$

3、Potter平方根滤波流程

4、向量量测情况下的方差阵量测更新

改量测更新就行，时间更新没必要改

前述标量量测情形

同理，向量量测情形：

全流程：

• 时间更新：$\Delta_{k-1} \stackrel{\mathrm{QR}}{\longrightarrow} \Delta_{k / k-1}$ ，要做一次QR分解
• 量测更新：$\boldsymbol{\Delta}{k / k-1} \stackrel{\mathrm{QR}}{\longrightarrow} \gamma{k} \stackrel{\text { 求逆 }}{\longrightarrow} \boldsymbol{\Delta}_{k}$ ，也要做一次QR分解（其实前面标量的开方也是QR分解）

三、奇异值（SVD）分解滤波

奇异值分解可以参考博客

$M=USV^T$，其中 $U$、$V$ 是正交矩阵，$S$ 是由 $M$ 的奇异值构成的对角矩阵。我们用奇异值分解的是方差阵，它对称正定。对称所以 $U$ 和 $V$ 相等，正定所以奇异值都大于 $0$

朴素分解方式：

上式每次更新要做两次QR分解，两次三角阵求逆；考虑用SVD分解，这样就只用做对角阵求逆。

1、时间更新方差方程的SVD分解

将方程的 $P_{k/k-1}$ 分解为 $\boldsymbol{U}{k / k-1} \boldsymbol{\Lambda}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}$ ，$P{k-1}$ 分解为 $\boldsymbol{U}{k-1} \boldsymbol{\Lambda}{ k-1} \boldsymbol{U}{ k-1}^{\mathrm{T}}$ ，选择合适的 $\boldsymbol{\Gamma}$ 噪声系数分配矩阵，可以认为 $Q$ 是对角阵。 $$ \begin{aligned}{l} \boldsymbol{U}{k / k-1} {\color{brown}\boldsymbol{\Lambda}{k / k-1}} \boldsymbol{U}{k / k-1}^{\mathrm{T}} & =\boldsymbol{\Phi}{k / k-1} \boldsymbol{U}{k-1} \boldsymbol{\Lambda}{k-1} \boldsymbol{U}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}} \ & =\left[\begin{array}{lll}\boldsymbol{\Phi}{k / k-1} \boldsymbol{U}{k-1} \boldsymbol{\Lambda}{k-1}^{\frac{1}{2}} & \boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1}^{\frac{1}{2}}\end{array}\right]\left[\begin{array}{c}\left(\boldsymbol{\Lambda}{k-1}^{\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{U}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}} \ \left(\boldsymbol{Q}{k-1}^{\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}}\end{array}\right] \end{aligned} $$ 再对矩阵做奇异值分解，得： $$ \begin{array}{l} =\left(\boldsymbol{S}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{V}{k / k-1}^{\mathrm{T}}\right)\left(\boldsymbol{S}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{V}{k / k-1}^{\mathrm{T}}\right)^{\mathrm{T}} \ =\boldsymbol{S}{k / k-1} {\color{brown}\boldsymbol{D}{k / k-1} \boldsymbol{D}{k / k-1}}^{\mathrm{T}} \boldsymbol{S}{k / k-1}^{\mathrm{T}} \end{array} $$ 此式与原式形式一致，令： $$ \boldsymbol{U}{k / k-1}=\boldsymbol{S}{k / k-1}, \boldsymbol{\Lambda}{k / k-1}^{\frac{1}{2}}=\boldsymbol{D}{k / k-1} $$

2、量测更新方差方程的SVD分解

同样，将方程的 $P_{k/k-1}$ 分解为 $\boldsymbol{U}{k / k-1} \boldsymbol{\Lambda}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}$ ，$P{k}$ 分解为 $\boldsymbol{U}{k} \boldsymbol{\Lambda}{ k} \boldsymbol{U}{ k}^{\mathrm{T}}$ ，得： $$ \boldsymbol{U}{k} \boldsymbol{\Lambda}{k}^{-1} \boldsymbol{U}{k}^{\mathrm{T}} =\boldsymbol{U}{k / k-1} \boldsymbol{\Lambda}{k / k-1}^{-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}+\boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{R}{k}^{-1} \boldsymbol{H}{k} \ =\left[\begin{array}{ll}\boldsymbol{U}{k / k-1} \boldsymbol{\Lambda}{k / k-1}^{-\frac{1}{2}} & \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{R}{k}^{-\frac{1}{2}}\end{array}\right]\left[\begin{array}{c}\left(\boldsymbol{\Lambda}{k / k-1}^{-\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \ \left(\boldsymbol{R}{k}^{-\frac{1}{2}}\right)^{\mathrm{T}} \boldsymbol{H}{k}\end{array}\right] $$ 对矩阵做SVD分解，得： $$ \begin{array}{l} =\left(\boldsymbol{S}{k} \boldsymbol{D}{k} \boldsymbol{V}{k}^{\mathrm{T}}\right)\left(\boldsymbol{S}{k} \boldsymbol{D}{k} \boldsymbol{V}{k}^{\mathrm{T}}\right)^{\mathrm{T}} =\boldsymbol{S}{k} \boldsymbol{D}{k} \boldsymbol{D}{k}^{\mathrm{T}} \boldsymbol{S}{k}^{\mathrm{T}} \end{array} $$ 也令： $$ \boldsymbol{U}{k}=\boldsymbol{S}{k}, \boldsymbol{\Lambda}{k}^{-\frac{1}{2}}=\boldsymbol{D}{k} $$

3、SVD分解滤波流程

$$ \begin{array}{l}\left(\boldsymbol{U}{k-1}, \boldsymbol{\Lambda}{k-1}^{\frac{1}{2}}, \boldsymbol{Q}{k-1}^{\frac{1}{2}}\right) \rightarrow\left[\boldsymbol{\Phi}{k / k-1} \boldsymbol{U}{k-1} \boldsymbol{\Lambda}{k-1}^{\frac{1}{2}} \quad \boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1}^{\frac{1}{2}}\right] \stackrel{\operatorname{SVD}}{\longrightarrow}\left(\boldsymbol{U}{k / k-1}, \boldsymbol{\Lambda}{k / k-1}^{\frac{1}{2}}\right) \ \rightarrow\left(\boldsymbol{U}{k / k-1}, \boldsymbol{\Lambda}{k / k-1}^{-\frac{1}{2}}, \boldsymbol{R}{k}^{-\frac{1}{2}}\right) \rightarrow\left[\boldsymbol{U}{k / k-1} \boldsymbol{\Lambda}{k / k-1}^{-\frac{1}{2}} \quad \boldsymbol{H}{k}^{\mathrm{T}} \boldsymbol{R}{k}^{-\frac{1}{2}}\right] \stackrel{\mathrm{SVD}}{\longrightarrow}\left(\boldsymbol{U}{k}, \boldsymbol{\Lambda}_{k}^{-\frac{1}{2}}\right) \rightarrow \cdots \\end{array} $$

每次更新含2次SVD分解、2次对角阵求逆，运算量与“朴素”方法相比没有明显优势（SVD分解计算量远大于QR），没啥用。

四、UD分解滤波

UD分解：$M=UDU^T$，$U$ 为上三角且对角线元素为 $1$，$D$ 为对角阵。存储的时候可以让 $U$ 占据上三角（对角线都是1），对角线上都为 $D$ 。

1、量测更新方差方程UD分解

必须是标量量测，向量的还没有人推导过，只能改成标量再分解

$$ \boldsymbol{P}{k}=\boldsymbol{P}{k / k-1}-\boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{P}{k / k-1} \boldsymbol{H}{k}^{\mathrm{T}}+R{k}\right)^{-1} \boldsymbol{H}{k} \boldsymbol{P}{k / k-1} $$

将方程的 $P_{k/k-1}$ 分解为 $\boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}$ ，$P{k}$ 分解为 $\boldsymbol{U}{k} \boldsymbol{D}{ k} \boldsymbol{U}{ k}^{\mathrm{T}}$，$R$ 为标量可以前后移动，得： $$ \begin{array}{l} \boldsymbol{U}{k} \boldsymbol{D}{k} \boldsymbol{U}{k}^{\mathrm{T}}= \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}- \ \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k}\right)^{-1} \boldsymbol{H}{k} \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \ = \boldsymbol{U}{k / k-1}\left[\boldsymbol{D}{k / k-1}-\boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}\left(\boldsymbol{H}{k} \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k}\right)^{-1} \boldsymbol{H}{k} \boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1}\right] \boldsymbol{U}{k / k-1}^{\mathrm{T}} \ = \boldsymbol{U}{k / k-1}\left(\boldsymbol{D}{k / k-1}-\alpha^{-1} \boldsymbol{g} \boldsymbol{g}^{\mathrm{T}}\right) \boldsymbol{U}{k / k-1}^{\mathrm{T}} \ \text { 记 }\left{\begin{array}{l}\alpha=\boldsymbol{H}{k} \boldsymbol{U}{k / k-1} \cdot \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}+R_{k}=\boldsymbol{f}^{\mathrm{T}} \boldsymbol{g}+R_{k} \ \boldsymbol{f}=\left(\boldsymbol{H}{k} \boldsymbol{U}{k / k-1}\right)^{\mathrm{T}} \ \boldsymbol{g}=\boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} \boldsymbol{H}{k}^{\mathrm{T}}=\boldsymbol{D}{k / k-1} \boldsymbol{f}\end{array}\right.\end{array} $$

从 $D_{nn}$ 开始先计算最后一列 ，再计算倒数第二列，直到 $D_{11}$ 。

2、时间更新方差方程UD分解

$$ \boldsymbol{P}{k / k-1}=\boldsymbol{\Phi}{k / k-1} \boldsymbol{P}{k-1} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} $$

将方程的 $P_{k/k-1}$ 分解为 $\boldsymbol{U}{k / k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}}$ ，$P{k-1}$ 分解为 $\boldsymbol{U}{k-1} \boldsymbol{D}{ k-1} \boldsymbol{U}{ k-1}^{\mathrm{T}}$ ，最后两边的矩阵记为 $\boldsymbol{W}{k \mid k-1}$ $$ \begin{aligned} \boldsymbol{U}{k \mid k-1} \boldsymbol{D}{k / k-1} \boldsymbol{U}{k / k-1}^{\mathrm{T}} & =\boldsymbol{\Phi}{k l k-1} \boldsymbol{U}{k-1} \boldsymbol{D}{k-1} \boldsymbol{U}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}{k-1} \boldsymbol{Q}{k-1} \boldsymbol{\Gamma}{k-1}^{\mathrm{T}} \ & =\left[\begin{array}{ll} \boldsymbol{\Phi}{k l k-1} \boldsymbol{U}{k-1} & \boldsymbol{\Gamma}{k-1} \end{array}\right]\left[\begin{array}{cc} \boldsymbol{D}{k-1} & \mathbf{0} \ \mathbf{0} & \boldsymbol{Q}{k-1} \end{array}\right]\left[\begin{array}{c} \boldsymbol{U}{k-1}^{\mathrm{T}} \boldsymbol{\Phi}{k l k-1}^{\mathrm{T}} \ \boldsymbol{\Gamma}{k-1}^{\mathrm{T}} \end{array}\right] \triangleq \boldsymbol{W}{k \mid k-1} \tilde{\boldsymbol{D}}{k-1} \boldsymbol{W}{k \mid k-1}^{\mathrm{T}} \end{aligned} $$

1.朴素算法

对 $\boldsymbol{W}{k \mid k-1}$ 再做一次QR分解： $$ \boldsymbol{W}{k l k-1} \tilde{\boldsymbol{D}}{k-1} \boldsymbol{W}{k / k-1}^{\mathrm{T}}=\hat{\boldsymbol{R}}^{\mathrm{T}} {\color{green}\hat{\boldsymbol{Q}}^{\mathrm{T}} \tilde{\boldsymbol{D}}{k-1} {\boldsymbol{Q}}} \hat{\boldsymbol{R}}=\hat{\boldsymbol{R}}^{\mathrm{T}} {\color{green}\boldsymbol{A}} \hat{\boldsymbol{R}} $$ 绿色部分正定对称，记为 $A$ ，对其进行UD分解： $$ =\hat{\boldsymbol{R}}^{\mathrm{T}} \hat{\boldsymbol{U}} \hat{\boldsymbol{D}} \hat{\boldsymbol{U}}^{\mathrm{T}} \overline{\boldsymbol{R}}=\left(\hat{\boldsymbol{R}}^{\mathrm{T}} \hat{\boldsymbol{U}}\right) \hat{\boldsymbol{D}}\left(\hat{\boldsymbol{R}}^{\mathrm{T}} \hat{\boldsymbol{U}}\right)^{\mathrm{T}} $$ $R$ 是QR分解出的三角阵，$U$ 是UD分解出的三角阵，乘出来的 $R^TU$ 还是三角阵，还有保证对角线是 $1$，把这部分赋给 $\boldsymbol{U}{k \mid k-1}$ ，不等于 $1$ 的部分归到 $D$ 里面。此方法要一次QR分解和一个UD分解，计算量大。

2.快速算法

用左边和右边元素一一对应得： $$ D_{k \mid k-1, j j}=\sum_{s=1}^{n+1} \tilde{D}{k-1, s s} W{j, s}^{(n-j)} W_{j, s}^{(n-j)} \quad U_{k l k-1, i j}=\frac{\sum_{s=1}^{n+1} \tilde{D}{k-1, s s} W{i, s}^{(n-j)} W_{j, s}^{(n-j)}}{D_{k / k-1, j j}} $$

滤波流程： $\left(U_{k-1, j,}, D_{k-1, j}\right) \rightarrow\left(U_{k \mid k-1, j j}, D_{k l k-1, j}\right) \rightarrow\left(U_{k, j}, D_{k, j, j}\right)$

运算量比较小，计算比较紧凑，已经推导好了一个一个元素怎么计算，比较实用。

五、平方根信息滤波SRIKF

将信息矩阵 $I$ 分解，与Potter平方根滤波很相似，计算量几乎一模一样，可以类比来看。