参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
本周讲解了贪心理论基础,以及第一道贪心的题目:贪心算法:分发饼干,可能会给大家一种贪心算法比较简单的错觉,好了,接下来几天的题目难度要上来了,哈哈。
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
- 输入: [1,7,4,9,2,5]
- 输出: 6
- 解释: 整个序列均为摆动序列。
示例 2:
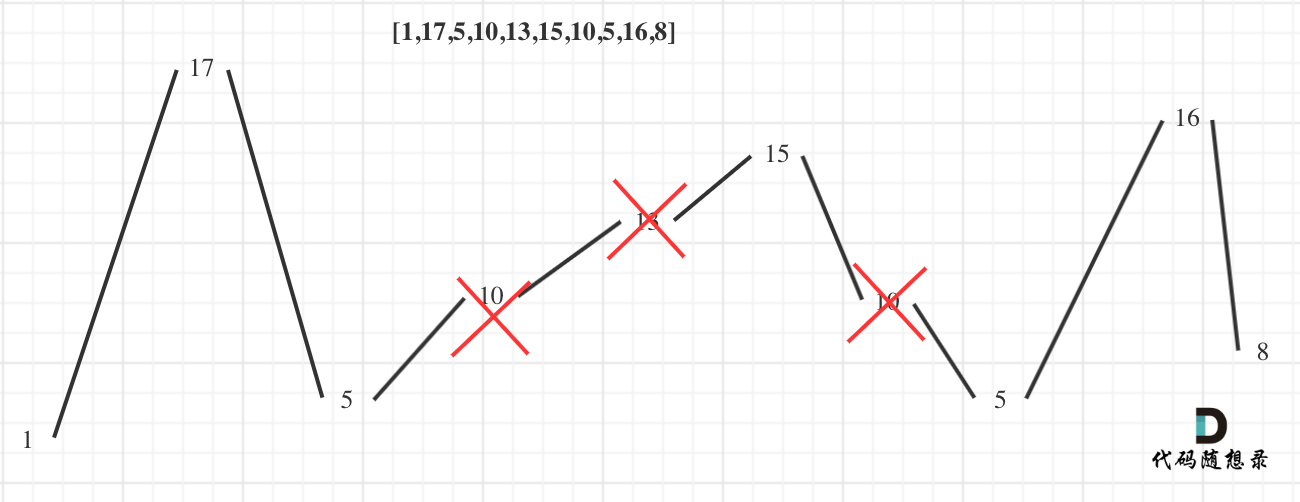
- 输入: [1,17,5,10,13,15,10,5,16,8]
- 输出: 7
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
示例 3:
- 输入: [1,2,3,4,5,6,7,8,9]
- 输出: 2
本题要求通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
相信这么一说吓退不少同学,这要求最大摆动序列又可以修改数组,这得如何修改呢?
来分析一下,要求删除元素使其达到最大摆动序列,应该删除什么元素呢?
用示例二来举例,如图所示:
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
局部最优推出全局最优,并举不出反例,那么试试贪心!
(为方便表述,以下说的峰值都是指局部峰值)
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点。
本题代码实现中,还有一些技巧,例如统计峰值的时候,数组最左面和最右面是最不好统计的。
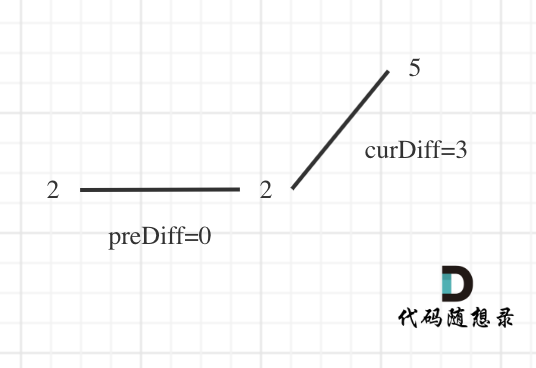
例如序列[2,5],它的峰值数量是2,如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
所以可以针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即preDiff = 0,如图:
针对以上情形,result初始为1(默认最右面有一个峰值),此时curDiff > 0 && preDiff <= 0,那么result++(计算了左面的峰值),最后得到的result就是2(峰值个数为2即摆动序列长度为2)
C++代码如下(和上图是对应的逻辑):
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // 当前一对差值
int preDiff = 0; // 前一对差值
int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 出现峰值
if ((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
preDiff = curDiff;
}
}
return result;
}
};- 时间复杂度:$O(n)$
- 空间复杂度:$O(1)$
考虑用动态规划的思想来解决这个问题。
很容易可以发现,对于我们当前考虑的这个数,要么是作为山峰(即nums[i] > nums[i-1]),要么是作为山谷(即nums[i] < nums[i - 1])。
- 设dp状态
dp[i][0],表示考虑前i个数,第i个数作为山峰的摆动子序列的最长长度 - 设dp状态
dp[i][1],表示考虑前i个数,第i个数作为山谷的摆动子序列的最长长度
则转移方程为:
dp[i][0] = max(dp[i][0], dp[j][1] + 1),其中0 < j < i且nums[j] < nums[i],表示将nums[i]接到前面某个山谷后面,作为山峰。dp[i][1] = max(dp[i][1], dp[j][0] + 1),其中0 < j < i且nums[j] > nums[i],表示将nums[i]接到前面某个山峰后面,作为山谷。
初始状态:
由于一个数可以接到前面的某个数后面,也可以以自身为子序列的起点,所以初始状态为:dp[0][0] = dp[0][1] = 1。
C++代码如下:
class Solution {
public:
int dp[1005][2];
int wiggleMaxLength(vector<int>& nums) {
memset(dp, 0, sizeof dp);
dp[0][0] = dp[0][1] = 1;
for (int i = 1; i < nums.size(); ++i)
{
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; ++j)
{
if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
}
for (int j = 0; j < i; ++j)
{
if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
}
}
return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
}
};- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$
进阶
可以用两棵线段树来维护区间的最大值
- 每次更新
dp[i][0],则在tree1的nums[i]位置值更新为dp[i][0] - 每次更新
dp[i][1],则在tree2的nums[i]位置值更新为dp[i][1] - 则dp转移方程中就没有必要j从0遍历到i-1,可以直接在线段树中查询指定区间的值即可。
时间复杂度:$O(n\log n)$
空间复杂度:$O(n)$
贪心的题目说简单有的时候就是常识,说难就难在都不知道该怎么用贪心。
本题大家如果要去模拟删除元素达到最长摆动子序列的过程,那指定绕里面去了,一时半会拔不出来。
而这道题目有什么技巧说一下子能想到贪心么?
其实也没有,类似的题目做过了就会想到。
此时大家就应该了解了:保持区间波动,只需要把单调区间上的元素移除就可以了。
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums == null || nums.length <= 1) {
return nums.length;
}
//当前差值
int curDiff = 0;
//上一个差值
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
//得到当前差值
curDiff = nums[i] - nums[i - 1];
//如果当前差值和上一个差值为一正一负
//等于0的情况表示初始时的preDiff
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
}// DP
class Solution {
public int wiggleMaxLength(int[] nums) {
// 0 i 作为波峰的最大长度
// 1 i 作为波谷的最大长度
int dp[][] = new int[nums.length][2];
dp[0][0] = dp[0][1] = 1;
for (int i = 1; i < nums.length; i++){
//i 自己可以成为波峰或者波谷
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; j++){
if (nums[j] > nums[i]){
// i 是波谷
dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
}
if (nums[j] < nums[i]){
// i 是波峰
dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
}
}
}
return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
}
}class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
preC,curC,res = 0,0,1 #题目里nums长度大于等于1,当长度为1时,其实到不了for循环里去,所以不用考虑nums长度
for i in range(len(nums) - 1):
curC = nums[i + 1] - nums[i]
if curC * preC <= 0 and curC !=0: #差值为0时,不算摆动
res += 1
preC = curC #如果当前差值和上一个差值为一正一负时,才需要用当前差值替代上一个差值
return resfunc wiggleMaxLength(nums []int) int {
var count,preDiff,curDiff int
count=1
if len(nums)<2{
return count
}
for i:=0;i<len(nums)-1;i++{
curDiff=nums[i+1]-nums[i]
//如果有正有负则更新下标值||或者只有前一个元素为0(针对两个不等元素的序列也视作摆动序列,且摆动长度为2)
if (curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0){
preDiff=curDiff
count++
}
}
return count
}贪心
var wiggleMaxLength = function(nums) {
if(nums.length <= 1) return nums.length
let result = 1
let preDiff = 0
let curDiff = 0
for(let i = 0; i < nums.length - 1; i++) {
curDiff = nums[i + 1] - nums[i]
if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
result++
preDiff = curDiff
}
}
return result
};动态规划
var wiggleMaxLength = function(nums) {
if (nums.length === 1) return 1;
// 考虑前i个数,当第i个值作为峰谷时的情况(则第i-1是峰顶)
let down = 1;
// 考虑前i个数,当第i个值作为峰顶时的情况(则第i-1是峰谷)
let up = 1;
for (let i = 1; i < nums.length; i++) {
if (nums[i] < nums[i - 1]) {
down = Math.max(up + 1, down);
}
if (nums[i] > nums[i - 1]) {
up = Math.max(down + 1, up)
}
}
return Math.max(down, up);
};