参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给定一个正整数 n,生成一个包含 1 到 $n^2$ 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
这道题目可以说在面试中出现频率较高的题目,本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。
要如何画出这个螺旋排列的正方形矩阵呢?
相信很多同学刚开始做这种题目的时候,上来就是一波判断猛如虎。
结果运行的时候各种问题,然后开始各种修修补补,最后发现改了这里哪里有问题,改了那里这里又跑不起来了。
大家还记得我们在这篇文章数组:每次遇到二分法,都是一看就会,一写就废中讲解了二分法,提到如果要写出正确的二分法一定要坚持循环不变量原则。
而求解本题依然是要坚持循环不变量原则。
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
可以发现这里的边界条件非常多,在一个循环中,如此多的边界条件,如果不按照固定规则来遍历,那就是一进循环深似海,从此offer是路人。
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开又闭的原则,这样这一圈才能按照统一的规则画下来。
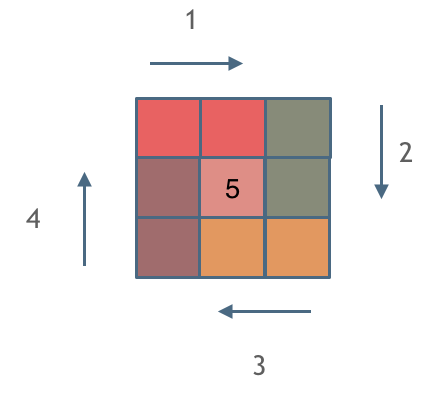
那么我按照左闭右开的原则,来画一圈,大家看一下:
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
这也是坚持了每条边左闭右开的原则。
一些同学做这道题目之所以一直写不好,代码越写越乱。
就是因为在画每一条边的时候,一会左开又闭,一会左闭右闭,一会又来左闭右开,岂能不乱。
代码如下,已经详细注释了每一步的目的,可以看出while循环里判断的情况是很多的,代码里处理的原则也是统一的左闭右开。
整体C++代码如下:
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组
int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理
int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)
int count = 1; // 用来给矩阵中每一个空格赋值
int offset = 1; // 每一圈循环,需要控制每一条边遍历的长度
int i,j;
while (loop --) {
i = startx;
j = starty;
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
for (j = starty; j < starty + n - offset; j++) {
res[startx][j] = count++;
}
// 模拟填充右列从上到下(左闭右开)
for (i = startx; i < startx + n - offset; i++) {
res[i][j] = count++;
}
// 模拟填充下行从右到左(左闭右开)
for (; j > starty; j--) {
res[i][j] = count++;
}
// 模拟填充左列从下到上(左闭右开)
for (; i > startx; i--) {
res[i][j] = count++;
}
// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
startx++;
starty++;
// offset 控制每一圈里每一条边遍历的长度
offset += 2;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};- 54.螺旋矩阵
- 剑指Offer 29.顺时针打印矩阵
Java:
class Solution {
public int[][] generateMatrix(int n) {
int[][] res = new int[n][n];
// 循环次数
int loop = n / 2;
// 定义每次循环起始位置
int startX = 0;
int startY = 0;
// 定义偏移量
int offset = 1;
// 定义填充数字
int count = 1;
// 定义中间位置
int mid = n / 2;
while (loop > 0) {
int i = startX;
int j = startY;
// 模拟上侧从左到右
for (; j<startY + n -offset; ++j) {
res[startX][j] = count++;
}
// 模拟右侧从上到下
for (; i<startX + n -offset; ++i) {
res[i][j] = count++;
}
// 模拟下侧从右到左
for (; j > startY; j--) {
res[i][j] = count++;
}
// 模拟左侧从下到上
for (; i > startX; i--) {
res[i][j] = count++;
}
loop--;
startX += 1;
startY += 1;
offset += 2;
}
if (n % 2 == 1) {
res[mid][mid] = count;
}
return res;
}
}python:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
# 初始化要填充的正方形
matrix = [[0] * n for _ in range(n)]
left, right, up, down = 0, n - 1, 0, n - 1
number = 1 # 要填充的数字
while left < right and up < down:
# 从左到右填充上边
for x in range(left, right):
matrix[up][x] = number
number += 1
# 从上到下填充右边
for y in range(up, down):
matrix[y][right] = number
number += 1
# 从右到左填充下边
for x in range(right, left, -1):
matrix[down][x] = number
number += 1
# 从下到上填充左边
for y in range(down, up, -1):
matrix[y][left] = number
number += 1
# 缩小要填充的范围
left += 1
right -= 1
up += 1
down -= 1
# 如果阶数为奇数,额外填充一次中心
if n % 2:
matrix[n // 2][n // 2] = number
return matrixjavaScript
/**
* @param {number} n
* @return {number[][]}
*/
var generateMatrix = function(n) {
let startX = startY = 0; // 起始位置
let loop = Math.floor(n/2); // 旋转圈数
let mid = Math.floor(n/2); // 中间位置
let offset = 1; // 控制每一层填充元素个数
let count = 1; // 更新填充数字
let res = new Array(n).fill(0).map(() => new Array(n).fill(0));
while (loop--) {
let row = startX, col = startY;
// 上行从左到右(左闭右开)
for (; col < startY + n - offset; col++) {
res[row][col] = count++;
}
// 右列从上到下(左闭右开)
for (; row < startX + n - offset; row++) {
res[row][col] = count++;
}
// 下行从右到左(左闭右开)
for (; col > startX; col--) {
res[row][col] = count++;
}
// 左列做下到上(左闭右开)
for (; row > startY; row--) {
res[row][col] = count++;
}
// 更新起始位置
startX++;
startY++;
// 更新offset
offset += 2;
}
// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值
if (n % 2 === 1) {
res[mid][mid] = count;
}
return res;
};
TypeScript:
function generateMatrix(n: number): number[][] {
let loopNum: number = Math.floor(n / 2);
const resArr: number[][] = new Array(n).fill(1).map(i => new Array(n));
let chunkNum: number = n - 1;
let startX: number = 0;
let startY: number = 0;
let value: number = 1;
let x: number, y: number;
while (loopNum--) {
x = startX;
y = startY;
while (x < startX + chunkNum) {
resArr[y][x] = value;
x++;
value++;
}
while (y < startY + chunkNum) {
resArr[y][x] = value;
y++;
value++;
}
while (x > startX) {
resArr[y][x] = value;
x--;
value++;
}
while (y > startY) {
resArr[y][x] = value;
y--;
value++;
}
startX++;
startY++;
chunkNum -= 2;
}
if (n % 2 === 1) {
resArr[startX][startY] = value;
}
return resArr;
};Go:
func generateMatrix(n int) [][]int {
top, bottom := 0, n-1
left, right := 0, n-1
num := 1
tar := n * n
matrix := make([][]int, n)
for i := 0; i < n; i++ {
matrix[i] = make([]int, n)
}
for num <= tar {
for i := left; i <= right; i++ {
matrix[top][i] = num
num++
}
top++
for i := top; i <= bottom; i++ {
matrix[i][right] = num
num++
}
right--
for i := right; i >= left; i-- {
matrix[bottom][i] = num
num++
}
bottom--
for i := bottom; i >= top; i-- {
matrix[i][left] = num
num++
}
left++
}
return matrix
}Swift:
func generateMatrix(_ n: Int) -> [[Int]] {
var result = [[Int]](repeating: [Int](repeating: 0, count: n), count: n)
var startRow = 0
var startColumn = 0
var loopCount = n / 2
let mid = n / 2
var count = 1
var offset = 1
var row: Int
var column: Int
while loopCount > 0 {
row = startRow
column = startColumn
for c in column ..< startColumn + n - offset {
result[startRow][c] = count
count += 1
column += 1
}
for r in row ..< startRow + n - offset {
result[r][column] = count
count += 1
row += 1
}
for _ in startColumn ..< column {
result[row][column] = count
count += 1
column -= 1
}
for _ in startRow ..< row {
result[row][column] = count
count += 1
row -= 1
}
startRow += 1
startColumn += 1
offset += 2
loopCount -= 1
}
if (n % 2) != 0 {
result[mid][mid] = count
}
return result
}Rust:
impl Solution {
pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
let mut res = vec![vec![0; n as usize]; n as usize];
let (mut startX, mut startY, mut offset): (usize, usize, usize) = (0, 0, 1);
let mut loopIdx = n/2;
let mid: usize = loopIdx as usize;
let mut count = 1;
let (mut i, mut j): (usize, usize) = (0, 0);
while loopIdx > 0 {
i = startX;
j = startY;
while j < (startY + (n as usize) - offset) {
res[i][j] = count;
count += 1;
j += 1;
}
while i < (startX + (n as usize) - offset) {
res[i][j] = count;
count += 1;
i += 1;
}
while j > startY {
res[i][j] = count;
count += 1;
j -= 1;
}
while i > startX {
res[i][j] = count;
count += 1;
i -= 1;
}
startX += 1;
startY += 1;
offset += 2;
loopIdx -= 1;
}
if(n % 2 == 1) {
res[mid][mid] = count;
}
res
}
}PHP:
class Solution {
/**
* @param Integer $n
* @return Integer[][]
*/
function generateMatrix($n) {
// 初始化数组
$res = array_fill(0, $n, array_fill(0, $n, 0));
$mid = $loop = floor($n / 2);
$startX = $startY = 0;
$offset = 1;
$count = 1;
while ($loop > 0) {
$i = $startX;
$j = $startY;
for (; $j < $startY + $n - $offset; $j++) {
$res[$i][$j] = $count++;
}
for (; $i < $startX + $n - $offset; $i++) {
$res[$i][$j] = $count++;
}
for (; $j > $startY; $j--) {
$res[$i][$j] = $count++;
}
for (; $i > $startX; $i--) {
$res[$i][$j] = $count++;
}
$startX += 1;
$startY += 1;
$offset += 2;
$loop--;
}
if ($n % 2 == 1) {
$res[$mid][$mid] = $count;
}
return $res;
}
}C:
int** generateMatrix(int n, int* returnSize, int** returnColumnSizes){
//初始化返回的结果数组的大小
*returnSize = n;
*returnColumnSizes = (int*)malloc(sizeof(int) * n);
//初始化返回结果数组ans
int** ans = (int**)malloc(sizeof(int*) * n);
int i;
for(i = 0; i < n; i++) {
ans[i] = (int*)malloc(sizeof(int) * n);
(*returnColumnSizes)[i] = n;
}
//设置每次循环的起始位置
int startX = 0;
int startY = 0;
//设置二维数组的中间值,若n为奇数。需要最后在中间填入数字
int mid = n / 2;
//循环圈数
int loop = n / 2;
//偏移数
int offset = 1;
//当前要添加的元素
int count = 1;
while(loop) {
int i = startX;
int j = startY;
//模拟上侧从左到右
for(; j < startY + n - offset; j++) {
ans[startX][j] = count++;
}
//模拟右侧从上到下
for(; i < startX + n - offset; i++) {
ans[i][j] = count++;
}
//模拟下侧从右到左
for(; j > startY; j--) {
ans[i][j] = count++;
}
//模拟左侧从下到上
for(; i > startX; i--) {
ans[i][j] = count++;
}
//偏移值每次加2
offset+=2;
//遍历起始位置每次+1
startX++;
startY++;
loop--;
}
//若n为奇数需要单独给矩阵中间赋值
if(n%2)
ans[mid][mid] = count;
return ans;
}