You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
After restoring your pretrained model and setting the random seed, I calculate the 3D coordinate error between y_t_xyz and y_p_xyz using the following L2-norm,
I remember the 3D joint positions L2 metric were evaluated with the following matlab script. We didn't scale the data but we performed Procrustes alignment, i.e. the global rotation and translation were set to 0 throughout.
And why the performance gain of eular error is not that large, compared with 3D coordinate error?
The Euler metric is not linear with respect to the 3D joint positions L2 metric. In fact the Euler mean angle error is not a geometrically meaningful metric (the geodesic error would be more geometrically meaningful in angular space whereas the L2 error would be good in 3D joint coordinates space). As such, we do not expect the performance gains between the two metrics to be linearly correlated.
After restoring your pretrained model and setting the random seed, I calculate the 3D coordinate error between y_t_xyz and y_p_xyz using the following L2-norm,
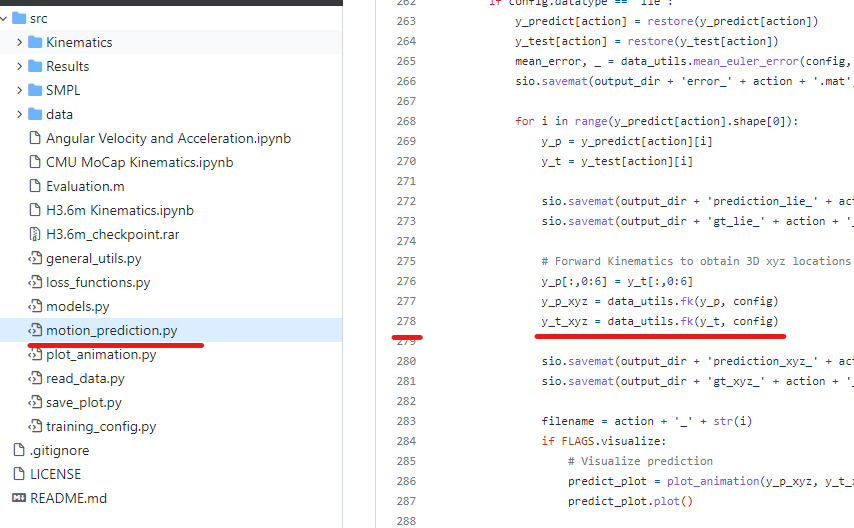
the results are larger than those in your paper, I want to know how do you calculate errors in 3D coordinate ? have you scaled the source data?
The text was updated successfully, but these errors were encountered: